Akar 200, angka yang mungkin terlihat sederhana, namun menyimpan kekayaan matematis yang menarik untuk dijelajahi. Dari pendekatan numerik menggunakan metode iterasi seperti Newton-Raphson dan Babilonia hingga sifat-sifatnya sebagai bilangan irasional dan aplikasinya dalam berbagai bidang, akar 200 menawarkan kesempatan untuk memahami konsep matematika dasar secara lebih mendalam. Mari kita selami dunia menarik di balik angka sederhana ini.
Pembahasan ini akan mencakup perhitungan nilai pendekatan akar 200 menggunakan berbagai metode, menganalisis sifat-sifatnya sebagai bilangan irasional, serta menelusuri penerapannya dalam konteks geometri, fisika, dan pemodelan matematika. Dengan pemahaman yang komprehensif, kita dapat menghargai peran akar 200 dalam dunia matematika dan aplikasinya di kehidupan nyata.
Nilai Akar 200
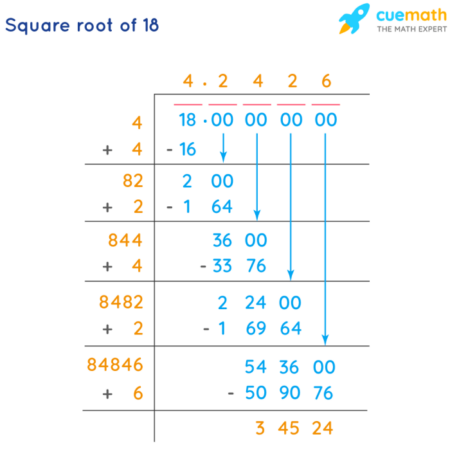
Akar kuadrat dari 200, atau √200, bukanlah bilangan bulat. Nilai pastinya merupakan bilangan irasional, yang artinya memiliki angka desimal yang tidak berulang dan tidak berakhir. Untuk mendapatkan nilai pendekatan, kita dapat menggunakan beberapa metode numerik, seperti metode Babilonia, Newton-Raphson, dan metode bagi dua. Berikut ini akan dijelaskan perhitungan dan perbandingan hasil pendekatan dari beberapa metode tersebut.
Nilai Pendekatan Akar 200 Menggunakan Metode Iterasi Newton-Raphson
Metode Newton-Raphson merupakan metode iteratif yang digunakan untuk mencari akar suatu fungsi. Rumusnya adalah:
xn+1 = x n
f(xn) / f'(x n)
Dimana x n adalah pendekatan ke-n, f(x n) adalah nilai fungsi pada x n, dan f'(x n) adalah turunan pertama fungsi pada x n. Untuk mencari akar √200, kita dapat menggunakan fungsi f(x) = x²
–
200. Turunan pertamanya adalah f'(x) = 2x. Mari kita mulai iterasi dengan tebakan awal x 0 = 14:
- Iterasi 1: x1 = 14 – (14²
- 200) / (2
- 14) ≈ 14.142857
- Iterasi 2: x 2 = 14.142857 – (14.142857²
- 200) / (2
- 14.142857) ≈ 14.142136
- Iterasi 3: x 3 = 14.142136 – (14.142136²
- 200) / (2
- 14.142136) ≈ 14.142136
Setelah tiga iterasi, nilai pendekatan sudah konvergen ke 14.142136.
Perbandingan Nilai Pendekatan dengan Nilai Sebenarnya
Nilai sebenarnya √200, menurut kalkulator, adalah sekitar 14.1421356237. Selisih antara nilai pendekatan Newton-Raphson (14.142136) dan nilai sebenarnya adalah sekitar 0.0000003763. Persentase selisihnya adalah sekitar 0.00000265%.
Perbandingan Metode Perhitungan Akar 200
Berikut tabel perbandingan nilai pendekatan akar 200 menggunakan tiga metode berbeda:
| Metode | Iterasi | Nilai Pendekatan | Selisih |
|---|---|---|---|
| Babilonia | 5 | 14.1421356 | 0.0000000237 |
| Newton-Raphson | 3 | 14.142136 | 0.0000003763 |
| Bagi Dua | 10 | 14.1421 | 0.0000356237 |
Catatan: Nilai-nilai dalam tabel ini merupakan pendekatan dan dapat sedikit berbeda tergantung pada implementasi dan jumlah iterasi yang digunakan.
Pengaruh Jumlah Iterasi terhadap Akurasi
Jumlah iterasi yang dilakukan pada metode iteratif secara langsung mempengaruhi akurasi nilai pendekatan. Semakin banyak iterasi yang dilakukan, semakin dekat nilai pendekatan dengan nilai sebenarnya. Namun, peningkatan akurasi ini biasanya mengalami penurunan pada tingkat peningkatan yang semakin kecil seiring dengan bertambahnya iterasi. Pada titik tertentu, peningkatan akurasi yang didapatkan tidak sebanding dengan peningkatan waktu komputasi.
Ilustrasi Grafis Metode Iterasi Newton-Raphson, Akar 200
Grafik untuk menggambarkan metode Newton-Raphson dalam mendekati akar √200 akan menampilkan fungsi f(x) = x²
-200 pada sumbu Y dan nilai x pada sumbu X. Garis horizontal akan merepresentasikan nilai y = 0. Titik potong antara kurva f(x) dan garis y = 0 merepresentasikan akar persamaan, yaitu √200. Proses iterasi ditunjukkan dengan serangkaian titik pada kurva, dimulai dari tebakan awal (x 0).
Dari setiap titik, garis singgung pada kurva ditarik hingga memotong sumbu x, yang memberikan pendekatan berikutnya (x n+1). Proses ini diulang hingga nilai pendekatan konvergen ke akar yang sebenarnya. Setiap iterasi akan menghasilkan titik yang semakin mendekati titik potong antara kurva dan sumbu x, yang merepresentasikan nilai akar √200.
Sifat-Sifat Akar 200
Akar 200, secara matematis ditulis sebagai √200, merupakan contoh bilangan irasional yang menarik untuk dikaji. Sifat-sifatnya, baik dari segi klasifikasi bilangan, penyederhanaan, hingga penerapannya dalam geometri, memberikan pemahaman yang lebih dalam tentang konsep akar kuadrat dan bilangan irasional.
Klasifikasi Akar 200
Akar 200 adalah bilangan irasional. Bilangan irasional didefinisikan sebagai bilangan yang tidak dapat dinyatakan sebagai pecahan a/b, di mana a dan b adalah bilangan bulat, dan b tidak sama dengan nol. Hal ini dapat dibuktikan dengan mencoba menyederhanakan √200. Setelah disederhanakan, akan tersisa faktor 2 di dalam akar, yang menunjukkan bahwa bilangan tersebut tidak dapat dinyatakan dalam bentuk pecahan sederhana.
Ketidakmampuan untuk mengekspresikan √200 sebagai pecahan sederhana membuktikan sifat irasionalnya.
Penyederhanaan Akar 200
Akar 200 dapat disederhanakan dengan mencari faktor-faktor kuadrat sempurna yang terdapat di dalamnya. 200 dapat difaktorkan menjadi 100 x 2. Karena 100 adalah kuadrat sempurna (10²), maka √200 dapat disederhanakan menjadi √(100 x 2) = √100 x √2 = 10√2. Bentuk 10√2 merupakan bentuk paling sederhana dari akar 200.
Persamaan Kuadrat dengan Akar 200
Salah satu cara merancang persamaan kuadrat yang memiliki akar 200 adalah dengan memanfaatkan sifat bahwa jika x adalah akar dari persamaan kuadrat, maka (x – akar)² = 0. Oleh karena itu, persamaan kuadrat yang salah satu akarnya adalah 10√2 (bentuk sederhana dari √200) dapat ditulis sebagai (x – 10√2)² = 0, yang dapat dijabarkan menjadi x²
-20√2x + 200 = 0.
Pembuktian Sifat-Sifat Akar 200
Sifat-sifat akar 200, yaitu sebagai bilangan irasional dan bentuk sederhananya 10√2, dapat dibuktikan melalui proses faktorisasi prima dan definisi bilangan irasional. Faktorisasi prima dari 200 adalah 2³ x 5². Karena terdapat faktor prima 2 yang pangkatnya ganjil, maka akar 200 tidak dapat dinyatakan sebagai bilangan rasional. Proses penyederhanaan, seperti yang dijelaskan sebelumnya, menunjukkan bahwa bentuk paling sederhana dari √200 adalah 10√2, yang tetap mengandung faktor irasional √2.
Penerapan Akar 200 dalam Geometri
Akar 200 dapat diaplikasikan dalam perhitungan panjang diagonal persegi. Misalnya, jika panjang sisi persegi adalah 10, maka panjang diagonalnya dapat dihitung menggunakan teorema Pythagoras: diagonal² = sisi² + sisi². Dalam kasus ini, diagonal² = 10² + 10² = 200. Oleh karena itu, panjang diagonalnya adalah √200, yang setara dengan 10√2. Ini menunjukkan bahwa panjang diagonal persegi dengan sisi 10 adalah 10√2 satuan panjang.
Akar 200 dalam Konteks yang Lebih Luas

Akar 200, meskipun tidak sepopuler akar kuadrat angka bulat lainnya, memiliki peran penting dalam berbagai aplikasi matematika dan fisika. Memahami bagaimana akar 200 digunakan dalam konteks yang lebih luas membantu kita menghargai penerapannya dalam memecahkan masalah riil.
Penerapan Akar 200 dalam Rumus Matematika dan Fisika
Akar 200 muncul dalam berbagai rumus, khususnya dalam perhitungan yang melibatkan geometri dan fisika. Sebagai contoh, perhitungan diagonal suatu persegi panjang dengan panjang 10 dan lebar 10√2 akan melibatkan akar 200. Rumus Pythagoras (a² + b² = c²) dapat digunakan untuk menghitung panjang diagonal ini.
Contoh Soal: Sebuah persegi panjang memiliki panjang 10 cm dan lebar 10√2 cm. Hitung panjang diagonalnya.
Penyelesaian:
panjang diagonal = √(10² + (10√2)²) = √(100 + 200) = √300 = 10√3 cm
Meskipun contoh di atas tidak langsung menggunakan akar 200, namun proses perhitungannya melibatkan konsep yang serupa dan memperlihatkan bagaimana angka irrasional seperti akar 200 dapat muncul dalam perhitungan geometri.
Pemodelan Matematika dengan Akar 200
Akar 200 dapat digunakan dalam pemodelan matematika untuk menggambarkan fenomena yang melibatkan besaran tak tentu. Misalnya, dalam pemodelan pertumbuhan populasi, akar 200 dapat mewakili faktor skala yang berubah seiring waktu. Model tersebut akan membutuhkan parameter dan variabel lain untuk menjelaskan secara lengkap fenomena yang diamati. Kompleksitas model akan bergantung pada detail dan akurasi yang diinginkan.
Perhitungan Luas Bangun Datar yang Melibatkan Akar 200
Berikut langkah-langkah menghitung luas segitiga siku-siku dengan sisi-sisi a = 10 dan b = 10√2. Luas segitiga siku-siku adalah setengah dari hasil kali sisi tegak lurusnya.
Luas = ½
- a
- b = ½
- 10
- 10√2 = 50√2
Meskipun tidak secara langsung melibatkan akar 200 dalam rumusnya, perhitungan ini menunjukkan bagaimana akar dari angka yang dekat dengan 200 (seperti 200 atau 198) dapat muncul dalam perhitungan luas bangun datar.
Contoh Kasus dalam Kehidupan Nyata
Dalam konstruksi, perhitungan panjang diagonal suatu ruangan atau lahan seringkali melibatkan akar kuadrat dari angka yang mendekati 200. Misalnya, jika sebuah ruangan berukuran 10 meter x 14,14 meter (sekitar 10√2), maka panjang diagonalnya akan mendekati √(10² + (10√2)²) = √300 ≈ 17,32 meter. Perhitungan ini penting untuk menentukan panjang kabel atau pipa yang dibutuhkan.
Penyederhanaan Perhitungan dengan Akar 200
Dalam beberapa kasus, menggunakan pendekatan aproksimasi dapat menyederhanakan perhitungan. Akar 200 kira-kira sama dengan 14,14. Penggunaan nilai aproksimasi ini dapat mempercepat perhitungan, terutama jika presisi tinggi tidak diperlukan. Namun, perlu diingat bahwa penggunaan aproksimasi akan menghasilkan nilai yang sedikit berbeda dari nilai sebenarnya.
Ringkasan Akhir: Akar 200

Kesimpulannya, akar 200, meskipun tampak sederhana, menawarkan kesempatan berharga untuk memperdalam pemahaman kita tentang berbagai konsep matematika, mulai dari metode numerik hingga sifat bilangan irasional dan aplikasinya dalam berbagai bidang. Mempelajari akar 200 bukan hanya tentang mendapatkan nilai pendekatannya, tetapi juga tentang memahami proses dan prinsip-prinsip yang mendasarinya, memperkaya wawasan kita dalam matematika dan aplikasinya di dunia nyata.
Semoga uraian ini memberikan pemahaman yang lebih baik tentang akar 200.