Rumus merasionalkan bentuk akar merupakan teknik penting dalam aljabar untuk menyederhanakan ekspresi matematika yang mengandung akar. Proses ini menghilangkan akar dari penyebut pecahan, menghasilkan bentuk yang lebih sederhana dan mudah diinterpretasi. Memahami rumus dan teknik merasionalkan bentuk akar sangat krusial, baik untuk menyelesaikan soal-soal aljabar maupun dalam penerapannya pada bidang lain seperti geometri dan kalkulus.
Artikel ini akan membahas secara detail pengertian merasionalkan bentuk akar, metode-metode yang digunakan, serta penerapannya dalam berbagai konteks. Dengan pemahaman yang komprehensif, Anda akan mampu menguasai teknik ini dan menyelesaikan berbagai permasalahan yang melibatkan bentuk akar dengan lebih efisien dan akurat.
Merasionalkan Bentuk Akar: Rumus Merasionalkan Bentuk Akar
Merasionalkan bentuk akar merupakan proses untuk menghilangkan akar dari penyebut suatu pecahan. Proses ini penting dalam matematika karena memudahkan perhitungan dan penyederhanaan ekspresi aljabar yang melibatkan akar. Bentuk akar yang sudah dirasionalkan akan lebih mudah diinterpretasikan dan dioperasikan, khususnya dalam konteks perhitungan numerik maupun aljabar lanjut.
Pada dasarnya, merasionalkan bentuk akar bertujuan untuk mengubah bentuk pecahan sehingga penyebutnya tidak lagi mengandung akar. Hal ini dicapai dengan mengalikan pembilang dan penyebut dengan suatu ekspresi yang tepat, sehingga akar pada penyebut akan hilang.
Bentuk Akar yang Perlu dan Tidak Perlu Dirasionalkan
Tidak semua bentuk akar perlu dirasionalkan. Bentuk akar yang perlu dirasionalkan umumnya adalah bentuk pecahan yang memiliki akar pada penyebutnya. Sedangkan bentuk akar yang sudah tidak memiliki akar pada penyebutnya atau bentuk akar yang berdiri sendiri (bukan pecahan) biasanya tidak perlu dirasionalkan.
- Contoh bentuk akar yang perlu dirasionalkan:
1/√2, 3/(√5 + 1), (2√3)/(√7 – 2)
- Contoh bentuk akar yang tidak perlu dirasionalkan:
√2, 3√5, 2 + √7
Perbedaan Bentuk Akar Rasional dan Irasional
Perbedaan utama terletak pada keberadaan akar pada penyebut pecahan. Bentuk akar rasional adalah bentuk yang tidak memiliki akar pada penyebutnya, sedangkan bentuk akar irasional memiliki akar pada penyebutnya. Bentuk akar rasional lebih sederhana dan mudah dioperasikan dibandingkan bentuk akar irasional.
Tabel Perbandingan Bentuk Akar Rasional dan Irasional
| Bentuk Akar | Rasional/Irasional | Penjelasan | Contoh |
|---|---|---|---|
| Pecahan dengan akar pada penyebut | Irasional | Penyebut mengandung akar, sehingga perlu dirasionalkan. | 1/√3 |
| Pecahan tanpa akar pada penyebut | Rasional | Penyebut tidak mengandung akar, sudah dalam bentuk paling sederhana. | 2/5 |
| Akar kuadrat sempurna | Rasional | Hasil akarnya adalah bilangan bulat atau pecahan biasa. | √9 = 3 |
| Akar kuadrat tidak sempurna | Irasional | Hasil akarnya adalah bilangan desimal yang tidak berulang. | √7 |
Konsep Dasar Merasionalkan Bentuk Akar
Konsep dasar merasionalkan bentuk akar adalah memanfaatkan sifat perkalian akar dan konsep bilangan konjugat. Untuk menghilangkan akar pada penyebut, kita mengalikan pembilang dan penyebut dengan suatu ekspresi yang menghasilkan bilangan rasional pada penyebut. Jika penyebut berupa √a, kita kalikan dengan √a/√a. Jika penyebut berupa a + √b, kita kalikan dengan konjugatnya, yaitu a – √b, dan sebaliknya.
Proses ini didasarkan pada identitas (a + b)(a – b) = a²
-b² yang menghilangkan akar pada penyebut.
(a + √b)(a – √b) = a² – b
Dengan demikian, kita menghilangkan akar dari penyebut tanpa mengubah nilai pecahan tersebut.
Merasionalkan Bentuk Akar: Rumus Merasionalkan Bentuk Akar
Merasionalkan bentuk akar merupakan proses menyederhanakan bentuk pecahan yang penyebutnya mengandung akar. Tujuannya adalah untuk menghilangkan akar dari penyebut sehingga bentuk pecahan menjadi lebih sederhana dan mudah dioperasikan dalam perhitungan matematika. Proses ini melibatkan perkalian dengan bentuk akar tertentu, baik akar tunggal, penjumlahan/pengurangan akar, maupun akar pangkat tiga.
Merasionalkan Bentuk Akar dengan Penyebut Akar Tunggal
Merasionalkan bentuk akar dengan penyebut berupa akar tunggal relatif sederhana. Langkah-langkahnya melibatkan perkalian pecahan tersebut dengan bentuk akar yang sama pada pembilang dan penyebut. Hal ini memanfaatkan sifat √a × √a = a.
Contoh: Rasionalkan 2/√5
Penyelesaian: Kalikan pembilang dan penyebut dengan √5:
(2/√5) × (√5/√5) = (2√5)/5
Merasionalkan Bentuk Akar dengan Penyebut Penjumlahan atau Pengurangan Akar
Merasionalkan bentuk akar dengan penyebut berupa penjumlahan atau pengurangan akar memerlukan teknik perkalian dengan bentuk sekawan. Bentuk sekawan dari (a + √b) adalah (a – √b), dan sebaliknya. Perkalian dengan bentuk sekawan memanfaatkan sifat (a + b)(a – b) = a²
-b² untuk menghilangkan akar pada penyebut.
Contoh: Rasionalkan 3/(2 + √3)
Penyelesaian: Kalikan pembilang dan penyebut dengan bentuk sekawan penyebut (2 – √3):
[3/(2 + √3)] × [(2 – √3)/(2 – √3)] = [3(2 – √3)] / [(2 + √3)(2 – √3)] = [6 – 3√3] / (4 – 3) = 6 – 3√3
Merasionalkan Bentuk Akar yang Melibatkan Perkalian Akar
Merasionalkan bentuk akar yang melibatkan perkalian akar dapat dilakukan dengan menyederhanakan bentuk akar terlebih dahulu sebelum melakukan proses merasionalkan. Sederhanakan perkalian akar tersebut menjadi bentuk akar yang paling sederhana kemudian ikuti langkah-langkah merasionalkan seperti di atas.
Contoh: Rasionalkan 6/(√2 × √8)
Penyelesaian: Sederhanakan penyebut terlebih dahulu: √2 × √8 = √16 = 4. Maka bentuknya menjadi 6/4 = 3/2. Bentuk ini sudah rasional.
Merasionalkan Bentuk Akar dengan Penyebut Bentuk Akar Pangkat Tiga
Merasionalkan bentuk akar pangkat tiga sedikit berbeda. Kita perlu mengalikan dengan bentuk yang menghasilkan bilangan rasional pada penyebut. Konsepnya mirip dengan merasionalkan akar kuadrat, hanya saja kita perlu mempertimbangkan pangkat tiga.
Contoh: Rasionalkan 2/∛5
Penyelesaian: Kalikan pembilang dan penyebut dengan ∛25:
(2/∛5) × (∛25/∛25) = (2∛25)/∛125 = (2∛25)/5
Perbedaan strategi merasionalkan akar bergantung pada bentuk penyebut. Untuk akar tunggal, cukup kalikan dengan akar itu sendiri. Untuk penjumlahan/pengurangan akar, gunakan bentuk sekawan. Untuk perkalian akar, sederhanakan terlebih dahulu. Dan untuk akar pangkat tiga, perlu perhitungan yang memastikan penyebut menjadi bilangan rasional.
Penerapan Merasionalkan Bentuk Akar

Merasionalkan bentuk akar, proses menghilangkan akar dari penyebut suatu pecahan, bukan hanya sekadar manipulasi aljabar. Teknik ini memiliki penerapan luas dalam berbagai bidang matematika, memudahkan penyederhanaan ekspresi dan penyelesaian masalah yang melibatkan akar.
Penyederhanaan Ekspresi Aljabar
Merasionalkan bentuk akar sangat berguna dalam menyederhanakan ekspresi aljabar yang kompleks. Dengan menghilangkan akar dari penyebut, kita memperoleh bentuk yang lebih sederhana dan mudah diinterpretasi. Contohnya, ekspresi 1/(√2 + 1)
dapat dirasionalkan dengan mengalikan pembilang dan penyebut dengan konjugat penyebut, yaitu (√2 – 1). Hasilnya adalah (√2 – 1)/1 = √2 – 1, yang merupakan bentuk yang lebih sederhana.
Penerapan dalam Geometri
Dalam geometri, merasionalkan bentuk akar sering muncul saat menghitung panjang sisi, luas, atau volume bangun geometri. Misalnya, saat menghitung diagonal sebuah persegi dengan sisi sepanjang ‘a’, kita akan memperoleh panjang diagonal √2a. Jika kita ingin menghitung luas segitiga dengan panjang sisi-sisinya melibatkan akar, merasionalkan bentuk akar akan memberikan hasil yang lebih akurat dan mudah dihitung.
- Menghitung panjang diagonal persegi panjang.
- Menghitung luas segitiga dengan sisi-sisi yang melibatkan akar.
- Menghitung volume kubus dengan diagonal ruang yang melibatkan akar.
Penggunaan dalam Kalkulus
Merasionalkan bentuk akar juga berperan penting dalam kalkulus, khususnya dalam limit dan integral. Seringkali, kita perlu menyederhanakan ekspresi yang mengandung akar sebelum melakukan operasi limit atau integral. Proses merasionalkan membantu menghilangkan bentuk tak tentu dan mempermudah perhitungan.
Contohnya, ketika menghitung limit fungsi yang mengandung akar, merasionalkan penyebut dapat menghilangkan bentuk tak tentu 0/0, yang memungkinkan kita untuk mengevaluasi limit tersebut.
Contoh Soal Cerita dan Penyelesaiannya
Sebuah taman berbentuk segitiga siku-siku dengan panjang sisi siku-sikunya 3√2 meter dan 4√2 meter. Berapakah luas taman tersebut?
- Menentukan rumus luas segitiga: Luas segitiga siku-siku = (1/2) x alas x tinggi.
- Mensubstitusikan nilai: Dalam kasus ini, alas = 3√2 meter dan tinggi = 4√2 meter. Maka, Luas = (1/2) x (3√2) x (4√2).
- Perkalian dan penyederhanaan: Luas = (1/2) x 12 x 2 = 12 meter persegi.
Dalam contoh ini, meskipun tidak secara eksplisit melibatkan merasionalkan penyebut, proses perkalian akar (√2 x √2 = 2) merupakan inti dari merasionalkan bentuk akar dan menyederhanakan hasil perhitungan.
Soal Latihan dan Pembahasan

Setelah mempelajari konsep merasionalkan bentuk akar, mari kita uji pemahaman Anda melalui beberapa soal latihan. Soal-soal berikut disusun dengan berbagai tingkat kesulitan untuk mengasah kemampuan Anda dalam merasionalkan berbagai bentuk akar. Pembahasan lengkap disertakan untuk membantu Anda memahami proses penyelesaian dan mengidentifikasi potensi kesalahan.
Lima Soal Latihan Merasionalkan Bentuk Akar
Berikut lima soal latihan yang mencakup berbagai tipe soal merasionalkan bentuk akar, dari yang sederhana hingga yang lebih kompleks. Perhatikan baik-baik setiap soal dan cobalah untuk menyelesaikannya sebelum melihat pembahasan.
- Rasionalkan bentuk akar √2/√3
- Rasionalkan bentuk akar (√5 + √2)/(√5 – √2)
- Rasionalkan bentuk akar (3√2 + 2√3)/(√6 – √2)
- Rasionalkan bentuk akar 1/(√5 + √2 – √3)
- Rasionalkan bentuk akar (√x + √y)/(√x – √y)
Pembahasan Soal Latihan
Berikut pembahasan lengkap untuk masing-masing soal latihan di atas. Pembahasan ini akan menjelaskan langkah-langkah penyelesaian secara detail sehingga Anda dapat memahami konsep merasionalkan bentuk akar dengan lebih baik.
- Penyelesaian soal nomor 1: Untuk merasionalkan √2/√3, kita kalikan pembilang dan penyebut dengan √3. Hasilnya adalah (√2√3)/(√3√3) = √6/3.
- Penyelesaian soal nomor 2: Untuk merasionalkan (√5 + √2)/(√5 – √2), kita kalikan pembilang dan penyebut dengan sekawan penyebut, yaitu (√5 + √2). Hasilnya adalah ((√5 + √2)(√5 + √2))/((√5 – √2)(√5 + √2)) = (5 + 2√10 + 2)/(5 – 2) = (7 + 2√10)/3.
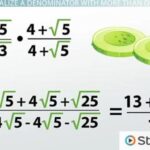
- Penyelesaian soal nomor 3: Untuk merasionalkan (3√2 + 2√3)/(√6 – √2), kita kalikan pembilang dan penyebut dengan sekawan penyebut, yaitu (√6 + √2). Langkah pertama, kita perlu mengalikan pembilang: (3√2 + 2√3)(√6 + √2) = 3√12 + 6 + 2√18 + 2√6 = 6√3 + 6 + 6√2 + 2√ Kemudian, kita kalikan penyebut: (√6 – √2)(√6 + √2) = 6 – 2 = 4. Jadi, hasil rasionalnya adalah (6√3 + 6 + 6√2 + 2√6)/4 = (3√3 + 3 + 3√2 + √6)/2.
- Penyelesaian soal nomor 4: Soal ini memerlukan pendekatan bertahap. Pertama, rasionalkan penyebut dengan mengalikan dengan sekawan dari (√5 + √2). Kemudian rasionalkan kembali penyebut yang dihasilkan dengan mengalikan sekawannya.
- Penyelesaian soal nomor 5: Mirip dengan soal nomor 2, kalikan pembilang dan penyebut dengan sekawan penyebut (√x + √y). Hasilnya akan berupa bentuk rasional yang melibatkan x dan y.
Ilustrasi Detail Penyelesaian Soal Nomor 3
Soal nomor 3, (3√2 + 2√3)/(√6 – √2), diselesaikan dengan mengalikan pembilang dan penyebut dengan sekawan penyebut yaitu (√6 + √2). Pertama, kita kalikan pembilang: (3√2 + 2√3)(√6 + √2) = 3√12 + 6 + 2√18 + 2√
6. Selanjutnya, kita sederhanakan setiap suku: 3√12 = 3(2√3) = 6√3; 2√18 = 2(3√2) = 6√
2. Jadi, pembilang menjadi 6√3 + 6 + 6√2 + 2√
6.
Kemudian, kita kalikan penyebut: (√6 – √2)(√6 + √2) = (√6)²
-(√2)² = 6 – 2 = 4. Akhirnya, hasil rasionalnya adalah (6√3 + 6 + 6√2 + 2√6)/4, yang dapat disederhanakan menjadi (3√3 + 3 + 3√2 + √6)/2.
Kesalahan Umum dalam Merasionalkan Bentuk Akar, Rumus merasionalkan bentuk akar
Kesalahan umum yang sering terjadi meliputi kesalahan dalam mengalikan bentuk akar, salah dalam menyederhanakan bentuk akar setelah merasionalkan, dan lupa mengalikan baik pembilang maupun penyebut dengan sekawannya. Kesalahan-kesalahan ini dapat menyebabkan hasil akhir yang salah.
Tips dan Trik Merasionalkan Bentuk Akar Secara Efisien
Untuk merasionalkan bentuk akar secara efisien, pastikan untuk memahami konsep sekawan dan cara mengalikannya dengan benar. Sederhanakan setiap suku setelah mengalikan untuk menghindari kesalahan perhitungan. Latihan rutin akan meningkatkan kecepatan dan keakuratan Anda dalam menyelesaikan soal-soal merasionalkan bentuk akar.
Kesimpulan
Merasionalkan bentuk akar, meskipun tampak rumit pada awalnya, merupakan keterampilan yang fundamental dalam matematika. Dengan memahami konsep dasar dan berbagai metode yang telah dijelaskan, Anda akan mampu mengatasi berbagai bentuk soal yang melibatkan akar. Kemampuan ini akan sangat bermanfaat tidak hanya dalam menyelesaikan soal-soal aljabar, tetapi juga dalam aplikasi praktis di bidang lain. Praktik dan latihan yang konsisten akan memperkuat pemahaman dan meningkatkan kemampuan Anda dalam merasionalkan bentuk akar dengan cepat dan akurat.