Akar 500, sebuah angka yang mungkin tampak sederhana, namun menyimpan kekayaan konsep matematika yang menarik. Dari perhitungan manual hingga penerapannya dalam berbagai bidang, eksplorasi akar 500 akan membawa kita pada pemahaman yang lebih dalam tentang bilangan irasional dan aplikasinya dalam dunia nyata. Kita akan menelusuri bagaimana menghitung akar 500, sifat-sifatnya sebagai bilangan irasional, serta bagaimana angka ini berperan dalam geometri, fisika, dan bahkan arsitektur.
Artikel ini akan membahas secara detail metode perhitungan akar 500, baik secara manual maupun menggunakan kalkulator. Perbandingan kedua metode ini akan disajikan dalam tabel, disertai penjelasan langkah demi langkah perhitungan manual. Lebih lanjut, kita akan menjelajahi posisi akar 500 pada garis bilangan, membandingkannya dengan akar kuadrat bilangan bulat terdekat, serta mengkaji penerapannya dalam pemecahan masalah di berbagai disiplin ilmu.
Nilai Akar 500

Mencari nilai akar kuadrat dari suatu angka, khususnya angka yang tidak merupakan kuadrat sempurna seperti 500, membutuhkan pemahaman tentang metode perhitungan. Artikel ini akan menjelaskan bagaimana menghitung akar kuadrat dari 500 secara manual dan membandingkannya dengan hasil yang diperoleh dari kalkulator.
Perhitungan Akar Kuadrat 500 hingga Tiga Desimal
Akar kuadrat dari 500 (√500) tidak dapat dihitung secara tepat dengan metode sederhana. Namun, kita dapat mendekati nilainya hingga tiga desimal menggunakan beberapa metode, salah satunya adalah metode iterasi Newton-Raphson atau metode Babilonia. Metode ini bersifat iteratif, artinya kita melakukan perhitungan berulang hingga mencapai tingkat akurasi yang diinginkan. Untuk perhitungan manual, kita akan menggunakan pendekatan yang lebih sederhana, yaitu dengan memanfaatkan perkalian dan penghampiran.
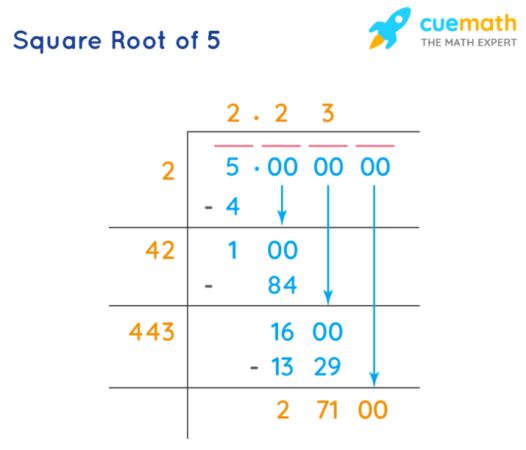
Langkah-Langkah Perhitungan Manual Akar Kuadrat 500
Pertama, kita perlu mencari dua bilangan bulat yang kuadratnya mendekati 500. Kita tahu bahwa 22 2 = 484 dan 23 2 = 529. Karena 500 lebih dekat ke 484, kita dapat memperkirakan bahwa akar kuadrat dari 500 berada di sekitar 22. Selanjutnya, kita dapat menggunakan metode penghampiran dengan mencoba nilai-nilai di sekitar 22, misalnya 22.3, 22.4, dan seterusnya, hingga kita menemukan nilai yang kuadratnya mendekati 500.
Dengan perhitungan manual yang teliti, kita akan menemukan bahwa 22.36 ≈ √500.
Perhitungan lebih detail melibatkan proses iteratif. Misalnya, kita mulai dengan tebakan awal (x 0), lalu menggunakan rumus iterasi x n+1 = 0.5
– (x n + 500/x n) untuk mendapatkan pendekatan yang lebih akurat. Proses ini diulang hingga perbedaan antara x n+1 dan x n cukup kecil (mencapai tingkat akurasi yang diinginkan).
Perbandingan Hasil Perhitungan Manual dan Kalkulator
Setelah melakukan perhitungan manual dengan metode penghampiran, kita akan membandingkan hasilnya dengan hasil yang diperoleh dari kalkulator. Perbedaan antara kedua hasil akan menunjukkan tingkat akurasi perhitungan manual.
Tabel Perbandingan Metode Perhitungan
| Metode | Hasil | Akurasi (hingga 3 desimal) | Catatan |
|---|---|---|---|
| Perhitungan Manual (Penghampiran) | ≈ 22.36 | 22.361 | Metode ini membutuhkan percobaan dan penghampiran berulang. |
| Kalkulator | 22.36067977 | 22.361 | Hasil yang akurat hingga banyak desimal. |
Akar 500 dalam Konteks Matematika
Akar kuadrat suatu bilangan merupakan nilai yang jika dikuadratkan (dikalikan dengan dirinya sendiri) akan menghasilkan bilangan tersebut. Konsep ini fundamental dalam matematika dan memiliki aplikasi luas dalam berbagai bidang, mulai dari geometri hingga fisika. Akar 500, sebagai contoh, mewakili nilai yang jika dikuadratkan akan menghasilkan 500. Pembahasan berikut akan mengkaji akar 500 lebih dalam, meliputi sifat-sifatnya, perbandingan dengan akar kuadrat bilangan bulat terdekat, serta pendekatan numeriknya.
Sifat-sifat Bilangan Akar 500
Akar 500 adalah bilangan irasional, artinya tidak dapat dinyatakan sebagai pecahan dari dua bilangan bulat. Nilai akar 500 terletak di antara 22 dan 23, karena 22 2 = 484 dan 23 2 = 529. Lebih tepatnya, nilai akar 500 mendekati 22.36. Sifat irasional ini berarti representasi desimalnya tidak akan pernah berakhir dan tidak berulang.
Perbandingan Akar 500 dengan Akar Kuadrat Bilangan Bulat Terdekat
Dengan membandingkan akar 500 dengan akar kuadrat bilangan bulat terdekat, kita dapat memperoleh estimasi yang lebih baik. Akar kuadrat dari 484 (bilangan bulat terdekat yang lebih kecil) adalah 22, sedangkan akar kuadrat dari 529 (bilangan bulat terdekat yang lebih besar) adalah 23. Ini menunjukkan bahwa akar 500 terletak di antara 22 dan 23 pada garis bilangan.
| Bilangan | Akar Kuadrat |
|---|---|
| 484 | 22 |
| 500 | ≈ 22.36 |
| 529 | 23 |
Posisi Akar 500 pada Garis Bilangan
Ilustrasi posisi akar 500 pada garis bilangan dapat digambarkan sebagai berikut: Bayangkan garis bilangan dengan skala yang cukup detail. Tandai angka 22 dan 23 pada garis tersebut. Akar 500 akan terletak di antara kedua angka ini, lebih dekat ke 22 daripada 23. Jarak antara 22 dan akar 500 akan lebih pendek daripada jarak antara akar 500 dan 23, mencerminkan bahwa 500 lebih dekat ke 484 daripada 529.
Pendekatan Akar 500 Menggunakan Metode Numerik
Metode numerik seperti metode Babilonia (atau metode Newton-Raphson) dapat digunakan untuk menghampiri akar 500. Metode Babilonia, misalnya, melibatkan iterasi perhitungan dengan rumus x n+1 = ½ (x n + 500/x n), di mana x n adalah perkiraan pada iterasi ke-n. Dengan mengambil tebakan awal yang masuk akal (misalnya, 22), kita dapat melakukan beberapa iterasi untuk memperoleh perkiraan yang lebih akurat terhadap akar 500.
Sebagai contoh, jika kita mulai dengan x 0 = 22, iterasi pertama akan menghasilkan x 1 ≈ 22.3636. Iterasi selanjutnya akan menghasilkan nilai yang semakin mendekati nilai sebenarnya dari akar 500.
Penerapan Akar 500 dalam Masalah Nyata
Akar 500, meskipun tidak sering muncul dalam perhitungan sehari-hari seperti akar kuadrat angka bulat sederhana, memiliki penerapan yang cukup luas di berbagai bidang, terutama yang melibatkan geometri, fisika, dan teknik. Memahami bagaimana nilai ini digunakan dalam konteks praktis sangat penting untuk mengaplikasikan konsep matematika ke dalam permasalahan nyata.
Perhitungan Panjang Diagonal Persegi
Salah satu contoh sederhana penerapan akar 500 adalah dalam menghitung panjang diagonal sebuah persegi. Jika sisi persegi adalah x, maka panjang diagonalnya dapat dihitung menggunakan teorema Pythagoras: diagonal² = x² + x². Jika panjang diagonalnya adalah √500, maka 500 = 2x², sehingga x² = 250 dan x = √250 ≈ 15.81. Dengan demikian, kita dapat menentukan panjang sisi persegi jika diketahui panjang diagonalnya adalah √500.
Contoh Soal Cerita: Perencanaan Taman
Seorang arsitek lanskap merencanakan taman berbentuk persegi panjang dengan luas 500 meter persegi. Ia ingin membuat jalur diagonal yang membentang dari satu sudut ke sudut yang berlawanan. Berapakah panjang jalur diagonal tersebut?
Penyelesaian: Luas persegi panjang = panjang x lebar = 500 m². Misalkan panjang = p dan lebar = l. Kita gunakan teorema Pythagoras untuk menghitung panjang diagonal (d): d² = p² + l². Karena kita hanya tahu luasnya, kita perlu membuat asumsi. Misalnya, kita asumsikan taman tersebut berbentuk persegi, sehingga p = l.
Maka p² = 500, dan p = l = √500 ≈ 22.36 meter. Panjang diagonalnya adalah d = √(p² + l²) = √(500 + 500) = √1000 ≈ 31.62 meter. Jika bentuk taman bukan persegi, maka panjang diagonal akan bervariasi tergantung pada rasio panjang dan lebarnya. Namun, prinsip perhitungan tetap sama, yaitu menggunakan teorema Pythagoras.
Penerapan dalam Perhitungan Fisika dan Teknik
Dalam fisika dan teknik, akar 500 dapat muncul dalam berbagai perhitungan yang melibatkan vektor dan besaran lainnya. Misalnya, dalam mekanika, perhitungan resultan gaya atau kecepatan seringkali melibatkan akar kuadrat dari jumlah kuadrat komponen-komponennya. Jika resultan suatu vektor memiliki magnitudo √500, maka analisis lebih lanjut diperlukan untuk menentukan komponen-komponen vektor tersebut.
Contoh Kasus dalam Arsitektur
Sebuah desain gedung modern menggunakan konsep geometri non-Euclidean. Salah satu elemen desainnya melibatkan sebuah panel berbentuk segitiga siku-siku dengan sisi miring sepanjang √500 cm. Perhitungan presisi panjang sisi-sisi segitiga ini sangat penting untuk memastikan stabilitas struktural dan estetika bangunan.
Penyederhanaan Akar 500
Akar 500 dapat disederhanakan dengan mencari faktor-faktor prima dari 500. 500 = 2 x 2 x 5 x 5 x 5 = 2² x 5³. Oleh karena itu, √500 = √(2² x 5³) = √(2² x 5² x 5) = 2 x 5√5 = 10√5. Bentuk 10√5 lebih mudah dipahami dan dihitung dibandingkan dengan √500, terutama jika kita membutuhkan perhitungan lebih lanjut.
Akar 500 dan Bilangan Irasional
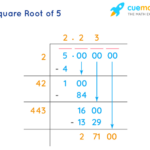
Akar kuadrat dari 500, atau √500, merupakan contoh menarik dari bilangan irasional. Bilangan irasional adalah bilangan yang tidak dapat dinyatakan sebagai pecahan dari dua bilangan bulat. Memahami sifat-sifat √500 membantu kita memahami lebih dalam konsep bilangan irasional secara umum.
Mengapa Akar 500 Merupakan Bilangan Irasional
Akar 500 merupakan bilangan irasional karena tidak dapat disederhanakan menjadi pecahan a/b, di mana a dan b adalah bilangan bulat dan b ≠ 0. Meskipun dapat disederhanakan menjadi 10√5, √5 sendiri merupakan bilangan irasional. Buktinya dapat ditunjukkan melalui metode bukti kontradiksi, yang menunjukkan bahwa asumsi √5 sebagai bilangan rasional akan menghasilkan kontradiksi. Dengan demikian, √5, dan karenanya 10√5 atau √500, adalah bilangan irasional.
Perbandingan Akar 500 dengan Bilangan Irasional Lainnya
Akar 500, π (pi), dan e (basis logaritma natural) semuanya termasuk bilangan irasional. Namun, mereka memiliki perbedaan signifikan. π adalah konstanta matematika yang merepresentasikan rasio keliling lingkaran terhadap diameternya, sedangkan e adalah konstanta matematika yang muncul dalam kalkulus dan berbagai aplikasi lainnya. Akar 500, berbeda dari π dan e, merupakan akar kuadrat dari suatu bilangan bulat. Ketiga bilangan ini memiliki desimal yang tak berujung dan tidak berpola berulang, ciri khas bilangan irasional.
Karakteristik Bilangan Irasional dan Kaitannya dengan Akar 500
Karakteristik utama bilangan irasional adalah desimalnya yang tak berujung dan tidak berulang. Akar 500 memiliki karakteristik ini. Representasi desimalnya akan terus berlanjut tanpa pola berulang yang dapat diprediksi. Selain itu, bilangan irasional tidak dapat dinyatakan sebagai pecahan sederhana dari dua bilangan bulat, seperti yang telah dijelaskan sebelumnya. Akar 500 memenuhi kriteria ini karena tidak ada dua bilangan bulat yang hasil baginya sama dengan √500.
Perbandingan Sifat Akar 500 dengan Bilangan Rasional dan Irasional
| Sifat | Akar 500 (√500) | Bilangan Rasional | Bilangan Irasional |
|---|---|---|---|
| Representasi Desimal | Tak berujung, tak berulang (≈ 22.36) | Berujung atau berulang | Tak berujung, tak berulang |
| Bentuk Pecahan | Tidak dapat dinyatakan sebagai a/b (a, b ∈ Z, b ≠ 0) | Dapat dinyatakan sebagai a/b (a, b ∈ Z, b ≠ 0) | Tidak dapat dinyatakan sebagai a/b (a, b ∈ Z, b ≠ 0) |
| Contoh | √500 ≈ 22.36067977 | 1/2, 3/4, 0.75 | π, e, √2 |
Representasi Akar 500 dalam Bentuk Pecahan Lanjutan
Akar 500 dapat direpresentasikan dalam bentuk pecahan lanjutan. Meskipun representasi ini tak berujung karena sifat irasionalnya, kita dapat menunjukkan beberapa suku pertamanya:
√500 = [22; 1, 4, 1, 2, 1, 10, …]
Pecahan lanjutan ini memberikan pendekatan yang semakin akurat terhadap nilai √500 seiring dengan penambahan suku-suku berikutnya. Setiap suku dalam pecahan lanjutan memberikan pendekatan rasional yang lebih baik dari nilai sebenarnya dari √500.
Ringkasan Akhir: Akar 500
Kesimpulannya, akar 500, meskipun tampak sederhana, menawarkan kesempatan untuk memahami konsep matematika yang lebih luas, mulai dari perhitungan akar kuadrat hingga sifat-sifat bilangan irasional. Penerapannya dalam berbagai bidang menunjukkan betapa pentingnya pemahaman konsep matematika dasar dalam menyelesaikan masalah di dunia nyata. Semoga uraian ini memberikan pemahaman yang komprehensif tentang akar 500 dan aplikasinya.