Akar 68, sebuah angka yang mungkin tampak sederhana, menyimpan banyak kejutan matematis. Eksplorasi nilai akar 68 membuka pintu menuju pemahaman yang lebih dalam tentang akar kuadrat, aplikasinya dalam berbagai bidang, dan bagaimana ia berinteraksi dengan bilangan-bilangan lain. Dari perhitungan manual hingga representasi visualnya pada garis bilangan, perjalanan memahami akar 68 ini akan memberikan wawasan yang berharga.
Kita akan menelusuri berbagai metode perhitungan akar 68, mulai dari pendekatan manual hingga penggunaan kalkulator. Lebih dari itu, kita akan melihat bagaimana akar 68 berperan dalam geometri, fisika, dan bahkan statistik. Dengan contoh-contoh konkret dan ilustrasi visual, kita akan mengungkap misteri yang tersembunyi di balik angka sederhana ini.
Nilai Akar 68
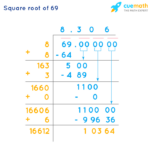
Akar kuadrat dari 68 bukanlah bilangan bulat, sehingga perhitungannya memerlukan pendekatan. Artikel ini akan membahas bagaimana menghitung nilai akar kuadrat 68 secara manual, menggunakan metode iteratif, dan membandingkannya dengan hasil kalkulator. Selain itu, kita akan mengulas konsep akar kuadrat dan aplikasinya, serta melihat perbandingan akar kuadrat beberapa bilangan di sekitar 68.
Perhitungan Manual Akar Kuadrat 68
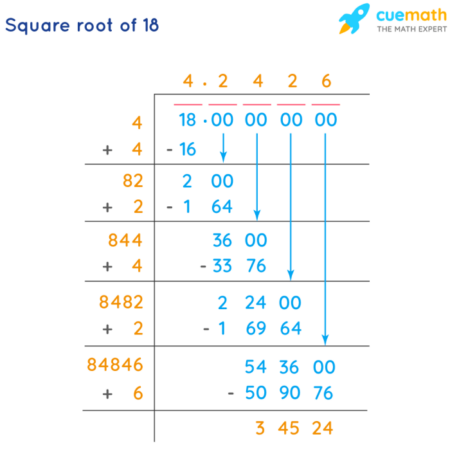
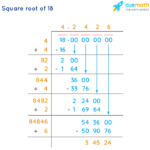
Menghitung akar kuadrat 68 secara manual dapat dilakukan dengan metode penaksiran. Kita tahu bahwa 8 2 = 64 dan 9 2 = 81. Oleh karena itu, akar kuadrat 68 berada di antara 8 dan 9. Untuk perhitungan yang lebih akurat, kita bisa menggunakan metode iteratif seperti metode Newton-Raphson, namun hal tersebut di luar cakupan perhitungan manual sederhana. Perkiraan awal yang masuk akal adalah 8,2 (karena 68 lebih dekat ke 64 daripada 81).
Pendekatan Akar 68 ke Satu Desimal Terdekat Menggunakan Metode Iteratif
Metode iteratif, seperti metode Babilonia (atau metode Heron), memberikan pendekatan yang lebih akurat. Metode ini dimulai dengan tebakan awal (misalnya, 8) dan secara berulang-ulang memperbaiki tebakan tersebut hingga mencapai tingkat akurasi yang diinginkan. Rumusnya adalah: x n+1 = 0.5
– (x n + 68/x n). Dengan tebakan awal x 0 = 8, kita dapat melakukan beberapa iterasi:
- x1 = 0.5 – (8 + 68/8) ≈ 8.25
- x 2 = 0.5 – (8.25 + 68/8.25) ≈ 8.246
Setelah beberapa iterasi, kita akan mendekati nilai akar 68 hingga satu desimal terdekat, yaitu 8.2.
Perbandingan Hasil Perhitungan Manual dan Kalkulator
Hasil perhitungan manual dengan metode iteratif memberikan nilai sekitar 8.2. Dengan menggunakan kalkulator, nilai akar kuadrat 68 adalah sekitar 8.2462112512. Perbedaannya relatif kecil, menunjukkan keakuratan metode iteratif yang digunakan.
Konsep Akar Kuadrat dan Aplikasinya
Akar kuadrat suatu bilangan adalah bilangan yang jika dikuadratkan (dikalikan dengan dirinya sendiri) menghasilkan bilangan tersebut. Konsep ini fundamental dalam matematika dan memiliki banyak aplikasi, termasuk dalam geometri (menghitung panjang sisi segitiga siku-siku dengan teorema Pythagoras), fisika (menghitung kecepatan, percepatan), dan berbagai bidang ilmu lainnya.
Perbandingan Akar Kuadrat Bilangan Terdekat dengan 68
Tabel berikut membandingkan akar kuadrat beberapa bilangan bulat terdekat dengan 68:
| Bilangan | Akar Kuadrat | Perbedaan dengan 68 | Perkiraan Desimal |
|---|---|---|---|
| 64 | 8 | -4 | 8.0 |
| 68 | ≈8.246 | 0 | 8.2 |
| 69 | ≈8.307 | 1 | 8.3 |
| 72 | ≈8.485 | 4 | 8.5 |
Representasi Akar 68
Akar 68, meskipun bukan bilangan bulat, dapat direpresentasikan dalam berbagai bentuk untuk memudahkan pemahaman dan penggunaannya dalam perhitungan matematika. Berikut beberapa representasi akar 68 beserta penjelasannya.
Akar 68 dalam Bentuk Desimal
Akar 68 dalam bentuk desimal dengan lima angka di belakang koma adalah 8.24621. Nilai ini didapatkan melalui perhitungan menggunakan kalkulator atau perangkat lunak matematika. Ketepatan angka di belakang koma dapat disesuaikan dengan kebutuhan perhitungan.
Akar 68 dalam Notasi Ilmiah
Representasi akar 68 dalam notasi ilmiah adalah 8.24621 x 10 0. Notasi ilmiah ini berguna untuk menyatakan bilangan yang sangat besar atau sangat kecil dengan cara yang lebih ringkas dan efisien.
Posisi Akar 68 pada Garis Bilangan
Akar 68 terletak pada garis bilangan di antara bilangan bulat 8 dan 9. Lebih tepatnya, akar 68 berada lebih dekat ke angka 8 karena nilainya 8.24621. Visualisasinya menunjukkan sebuah titik yang berada sekitar seperempat jarak antara 8 dan 9.
Faktorisasi Akar 68
Akar 68 dapat diekspresikan sebagai perkalian dari faktor-faktornya. Karena 68 = 4 x 17, maka akar 68 dapat ditulis sebagai √(4 x 17) atau √4 x √17, yang dapat disederhanakan menjadi 2√17. Ini menunjukkan bahwa akar 68 merupakan perkalian dari 2 dan akar 17.
Ilustrasi Akar 68 pada Garis Bilangan
Bayangkan sebuah garis bilangan dengan skala yang menunjukkan bilangan bulat dari 7 hingga 10. Tandai bilangan bulat 8 dan 9 pada garis tersebut. Kemudian, tandai sebuah titik di antara 8 dan 9, lebih dekat ke 8. Titik ini merepresentasikan posisi akar 68 (sekitar 8.24621). Jarak antara 8 dan titik tersebut kira-kira seperempat dari jarak antara 8 dan 9.
Skala pada garis bilangan dapat disesuaikan untuk memperlihatkan detail posisi akar 68 dengan lebih jelas. Penanda dapat berupa titik kecil atau tanda lain yang jelas untuk menunjukan lokasi akar 68.
Penggunaan Akar 68 dalam Konteks
Akar kuadrat dari 68, atau √68, merupakan bilangan irasional yang memiliki banyak aplikasi dalam berbagai bidang, terutama dalam matematika, fisika, dan statistika. Memahami bagaimana bilangan ini digunakan dalam konteks yang berbeda sangat penting untuk memperluas pemahaman kita tentang konsep akar kuadrat dan penerapannya dalam pemecahan masalah.
Penerapan Akar 68 dalam Perhitungan Geometri
Akar 68 dapat muncul dalam perhitungan geometri, khususnya dalam menentukan panjang sisi segitiga siku-siku. Misalnya, jika kita memiliki segitiga siku-siku dengan panjang sisi siku-sikunya a dan b, dan panjang sisi miringnya c, maka berdasarkan teorema Pythagoras, berlaku rumus c² = a² + b². Jika kita mengetahui nilai a dan b, kita dapat menghitung c. Sebaliknya, jika kita mengetahui nilai c dan salah satu sisi siku-siku, kita dapat menghitung sisi siku-siku lainnya.
Sebagai contoh, jika panjang sisi miring (c) adalah 10 dan salah satu sisi siku-siku (a) adalah 6, maka panjang sisi siku-siku lainnya (b) dapat dihitung sebagai berikut:
b² = c²
- a² = 10²
- 6² = 100 – 36 = 64. Oleh karena itu, b = √64 = 8.
Namun, jika panjang sisi miring (c) adalah 10 dan salah satu sisi siku-siku (a) adalah 2, maka panjang sisi siku-siku lainnya (b) akan menjadi √(10²
-2²) = √96. √96 dapat disederhanakan menjadi √(16 x 6) = 4√6. Jika kita memiliki segitiga siku-siku dengan sisi miring 10 dan sisi siku-siku 6, maka sisi siku-siku lainnya adalah √68.
Penggunaan Akar 68 dalam Pemecahan Masalah Fisika
Dalam fisika, akar 68 dapat muncul dalam berbagai persamaan, misalnya dalam perhitungan kecepatan, percepatan, atau jarak. Sebagai contoh, bayangkan sebuah proyektil diluncurkan dengan kecepatan awal tertentu dan sudut elevasi tertentu. Komponen kecepatan vertikal dan horizontal proyektil dapat dihitung menggunakan trigonometri, dan akar 68 bisa muncul dalam perhitungan jarak tempuh horizontal atau waktu tempuh.
Sebagai ilustrasi sederhana (walaupun mungkin tidak realistis untuk menghasilkan akar 68 secara langsung), andaikan sebuah benda jatuh bebas dari ketinggian tertentu. Jika kita ingin menghitung kecepatan benda tersebut tepat sebelum menyentuh tanah, kita dapat menggunakan rumus v = √(2gh), dimana v adalah kecepatan akhir, g adalah percepatan gravitasi, dan h adalah ketinggian. Jika kita mendapatkan hasil perhitungan √(2gh) = √68 m/s, maka kecepatan akhir benda tersebut adalah √68 m/s.
Kemunculan Akar 68 dalam Konteks Statistika atau Probabilitas
Akar 68 dapat muncul dalam konteks statistika atau probabilitas, khususnya dalam perhitungan standar deviasi atau varians dari suatu distribusi data. Standar deviasi mengukur sebaran data di sekitar rata-rata. Dalam distribusi normal, sekitar 68% data terletak dalam satu standar deviasi dari rata-rata. Meskipun √68 sendiri mungkin tidak secara langsung muncul sebagai standar deviasi dalam contoh kasus umum, nilai ini bisa menjadi bagian dari perhitungan yang lebih kompleks yang melibatkan standar deviasi atau varians.
Misalnya, bayangkan kita memiliki kumpulan data dengan varians 68. Standar deviasi dari data tersebut adalah √68. Konsep ini penting untuk memahami sebaran data dan untuk membuat kesimpulan statistik.
Contoh Soal Matematika yang Melibatkan Akar 68
Sebuah persegi panjang memiliki panjang diagonal 10 cm dan lebar 6 cm. Berapakah panjang sisi persegi panjang tersebut?
Penyelesaian:
Kita dapat menggunakan teorema Pythagoras. Misalkan panjang sisi persegi panjang adalah x. Maka x² + 6² = 10². Dengan demikian, x² = 100 – 36 = 64. Jadi, x = √64 = 8 cm.
Namun, jika panjang diagonalnya 10 cm dan lebarnya 2 cm, maka panjangnya adalah √(10²
-2²) = √96 = 4√6 cm. Jika panjang diagonalnya adalah 10 cm dan lebarnya 6 cm, maka panjang sisinya adalah √68 cm.
Pentingnya Memahami Konsep Akar Kuadrat
Memahami konsep akar kuadrat sangat penting dalam berbagai bidang ilmu. Kemampuan untuk menghitung dan menginterpretasikan akar kuadrat memungkinkan kita untuk menyelesaikan masalah dalam geometri, fisika, statistika, dan banyak bidang lainnya. Akar kuadrat merupakan fondasi untuk pemahaman konsep-konsep matematika yang lebih lanjut dan penerapannya dalam kehidupan nyata.
Perbandingan dengan Akar Lain
Akar kuadrat dari 68, sekitar 8.246, terletak di antara akar kuadrat dari bilangan bulat terdekat, yaitu akar 64 (8) dan akar 81 (9). Perbandingan ini memungkinkan kita untuk memahami bagaimana nilai akar kuadrat berubah seiring perubahan bilangan pokok dan dampaknya terhadap berbagai perhitungan.
Perbedaan antara akar-akar ini, meskipun tampak kecil secara numerik, mempunyai implikasi signifikan dalam konteks aplikasi praktis. Misalnya, dalam geometri, perbedaan ini bisa berdampak pada perhitungan luas atau panjang diagonal.
Perbedaan Nilai Akar dan Dampaknya
Perbedaan antara √68 (≈8.246), √64 (8), dan √81 (9) menunjukkan bagaimana perubahan kecil pada bilangan pokok dapat menghasilkan perubahan yang relatif lebih besar pada akar kuadratnya. Perbedaan antara √68 dan √64 sekitar 0.246, sedangkan perbedaan antara √81 dan √68 sekitar 0.754. Dalam konteks perhitungan luas persegi, perbedaan ini akan berdampak pada hasil akhir. Misalnya, jika sisi persegi adalah √68 unit, luasnya akan berbeda dibandingkan dengan persegi yang memiliki sisi √64 atau √81 unit.
Dalam konteks fisika, perbedaan ini bisa mewakili variasi dalam besaran seperti kecepatan atau percepatan, di mana perbedaan kecil dapat berakibat signifikan pada hasil akhir perhitungan.
Pola dan Tren Perbandingan Akar Kuadrat
Secara umum, perbandingan akar kuadrat menunjukkan tren bahwa peningkatan bilangan pokok akan menghasilkan peningkatan nilai akar kuadratnya, tetapi peningkatan tersebut tidak linier. Perubahan pada akar kuadrat semakin kecil seiring dengan meningkatnya nilai bilangan pokok. Hal ini dapat diamati dengan membandingkan perbedaan antara √64 dan √68 dengan perbedaan antara √81 dan √68; perbedaan yang terakhir lebih besar.
Grafik Perbandingan Akar Kuadrat
Grafik yang menampilkan perbandingan nilai akar kuadrat dari beberapa bilangan bulat di sekitar 68 akan berupa kurva yang naik secara monoton. Sumbu X akan mewakili bilangan bulat (misalnya, dari 60 hingga 80), sedangkan sumbu Y akan mewakili nilai akar kuadratnya. Kurva akan menunjukkan peningkatan yang semakin landai seiring dengan meningkatnya nilai bilangan bulat. Grafik ini akan secara visual mengilustrasikan hubungan non-linier antara bilangan pokok dan akar kuadratnya.
Titik-titik data akan menunjukkan nilai akar kuadrat dari bilangan bulat tertentu, dan kurva akan menghubungkan titik-titik tersebut untuk menunjukkan tren keseluruhan.
Perbedaan Akar Kuadrat dan Akar Pangkat Tiga dari 68
Akar kuadrat dari 68 mencari bilangan yang, jika dikuadratkan, menghasilkan 68. Sedangkan akar pangkat tiga dari 68 mencari bilangan yang, jika dipangkatkan tiga, menghasilkan 68. Nilai akar kuadrat dari 68 (≈8.246) secara signifikan lebih besar daripada akar pangkat tiga dari 68 (≈4.082). Perbedaan ini muncul karena pangkat tiga menghasilkan nilai yang meningkat lebih cepat daripada pangkat dua. Semakin tinggi pangkatnya, semakin besar perbedaan antara nilai akarnya untuk bilangan yang sama.
Penutup
Perjalanan kita menelusuri akar 68 telah menunjukkan betapa angka sederhana ini dapat membuka pintu menuju pemahaman yang lebih dalam tentang konsep matematika fundamental. Dari perhitungan manual hingga aplikasinya di berbagai bidang, akar 68 telah membuktikan dirinya sebagai elemen kunci dalam berbagai perhitungan dan pemecahan masalah. Semoga pemahaman yang lebih baik tentang akar 68 ini dapat menginspirasi eksplorasi lebih lanjut dalam dunia matematika.