Akar persamaan, inti dari berbagai permasalahan matematika dan sains, merupakan nilai-nilai yang memenuhi suatu persamaan. Memahami akar persamaan sangat krusial, karena merupakan kunci untuk memecahkan berbagai masalah dalam berbagai disiplin ilmu, mulai dari teknik sipil hingga ekonomi. Dari persamaan linear sederhana hingga persamaan polinomial tingkat tinggi, pencarian akarnya melibatkan beragam metode dan teknik yang menarik untuk dipelajari.
Artikel ini akan membahas secara komprehensif konsep akar persamaan, metode pencariannya, aplikasinya di berbagai bidang, serta bagaimana menginterpretasikan hasil yang diperoleh. Kita akan menjelajahi metode numerik, analisis persamaan berbagai derajat, dan implikasi dari akar-akar yang ditemukan dalam konteks masalah nyata.
Pengertian Akar Persamaan
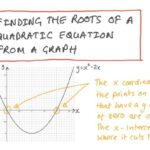
Akar persamaan, dalam matematika, merujuk pada nilai variabel yang memenuhi persamaan tersebut. Dengan kata lain, akar persamaan adalah solusi dari persamaan. Menemukan akar persamaan merupakan langkah penting dalam menyelesaikan berbagai masalah matematika dan ilmu terapan.
Sebagai contoh, perhatikan persamaan linear sederhana: x + 2 = 5. Akar dari persamaan ini adalah x = 3, karena jika kita substitusikan x = 3 ke dalam persamaan, maka persamaan tersebut menjadi 3 + 2 = 5, yang merupakan pernyataan benar. Persamaan yang lebih kompleks dapat memiliki lebih dari satu akar, bahkan akar yang berupa bilangan kompleks.
Perbedaan Akar Persamaan Linear dan Non-Linear
Persamaan linear ditandai dengan pangkat tertinggi variabelnya adalah satu. Akar persamaan linear selalu tunggal. Sementara itu, persamaan non-linear memiliki pangkat tertinggi variabel lebih dari satu. Persamaan non-linear dapat memiliki beberapa akar, baik akar riil maupun akar kompleks (imajiner).
Sebagai contoh, x + 5 = 0 merupakan persamaan linear dengan akar x = -5. Sedangkan x²
-4 = 0 merupakan persamaan non-linear dengan akar x = 2 dan x = -2.
Perbandingan Metode Pencarian Akar Berbagai Jenis Persamaan
Berbagai metode digunakan untuk mencari akar persamaan, tergantung pada derajat dan jenis persamaan. Berikut tabel perbandingan untuk beberapa jenis persamaan:
| Jenis Persamaan | Derajat Persamaan | Metode Pencarian Akar | Contoh |
|---|---|---|---|
| Persamaan Linear | 1 | Metode aljabar sederhana (isolasi variabel) | x + 5 = 0 |
| Persamaan Kuadrat | 2 | Rumus kuadratik, pemfaktoran, melengkapi kuadrat | x² – 5x + 6 = 0 |
| Persamaan Kubik | 3 | Rumus kubik (rumus Cardano), metode numerik (misalnya, metode Newton-Raphson) | x³
|
| Persamaan Polinomial Tingkat Tinggi (n > 3) | n | Metode numerik (misalnya, metode Newton-Raphson, metode biseksi), faktorisasi jika memungkinkan | x⁴
|
Persamaan dengan Akar Imajiner atau Kompleks
Beberapa persamaan, terutama persamaan polinomial dengan derajat genap, dapat memiliki akar imajiner atau kompleks. Akar-akar ini merupakan bilangan kompleks yang terdiri dari bagian riil dan bagian imajiner, ditulis dalam bentuk a + bi, di mana ‘a’ dan ‘b’ adalah bilangan riil, dan ‘i’ adalah satuan imajiner (√-1).
Contohnya, persamaan kuadrat x² + 1 = 0 memiliki akar x = i dan x = -i. Persamaan ini tidak memiliki akar riil karena tidak ada bilangan riil yang kuadratnya sama dengan -1. Metode pencarian akar untuk persamaan yang memiliki akar kompleks biasanya melibatkan bilangan kompleks dan seringkali memerlukan metode numerik.
Metode Mencari Akar Persamaan
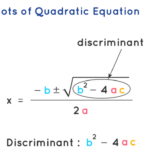
Mencari akar persamaan, yaitu nilai x yang membuat f(x) = 0, merupakan permasalahan umum dalam berbagai bidang ilmu, mulai dari matematika dan fisika hingga ekonomi dan teknik. Terdapat berbagai metode untuk menyelesaikannya, mulai dari metode analitik yang menghasilkan solusi eksak hingga metode numerik yang memberikan aproksimasi solusi. Metode numerik sangat berguna ketika metode analitik tidak memungkinkan atau terlalu rumit untuk diterapkan.
Metode Numerik Pencarian Akar Persamaan
Metode numerik menawarkan pendekatan iteratif untuk menemukan akar persamaan. Metode ini menghasilkan hampiran akar yang semakin akurat dengan setiap iterasi. Dua metode yang umum digunakan adalah metode biseksi dan metode Newton-Raphson.
- Metode Biseksi: Metode ini bekerja dengan membagi interval yang diketahui mengandung akar menjadi dua bagian secara berulang. Interval yang baru dipilih akan selalu mengandung akar, sehingga akar tersebut diapit secara bertahap. Proses ini berlanjut hingga mencapai tingkat akurasi yang diinginkan.
- Metode Newton-Raphson: Metode ini menggunakan turunan pertama fungsi untuk memperkirakan akar dengan lebih cepat daripada metode biseksi. Rumusnya didasarkan pada pendekatan linear fungsi di sekitar titik tebakan awal. Metode ini bersifat konvergen kuadratik, artinya tingkat konvergensinya lebih cepat daripada metode biseksi.
Contoh Penerapan Metode Iterasi
Misalkan kita ingin mencari akar persamaan f(x) = x³
-2x – 5 = 0. Kita akan menggunakan metode iterasi Newton-Raphson. Turunan pertama fungsi tersebut adalah f'(x) = 3x²
–
2. Dengan tebakan awal x₀ = 2, iterasi pertama akan menghasilkan:
- x₁ = x₀
- f(x₀) / f'(x₀) = 2 – (2³
- 2(2)
- 5) / (3(2)²
- 2) = 2 – (-1) / 10 = 2.1
- Iterasi selanjutnya dilakukan dengan mengganti x₀ dengan x₁ dan seterusnya hingga mencapai tingkat akurasi yang diinginkan.
Metode biseksi dapat diterapkan dengan menentukan interval yang mengandung akar, misalnya [2, 3], dan kemudian membagi interval tersebut berulang kali.
Perbandingan Efisiensi Metode Pencarian Akar
Metode Newton-Raphson umumnya lebih efisien daripada metode biseksi karena konvergensinya yang lebih cepat. Namun, metode Newton-Raphson membutuhkan perhitungan turunan pertama fungsi, yang mungkin rumit atau tidak mungkin untuk beberapa fungsi. Metode biseksi lebih sederhana dan selalu konvergen, tetapi konvergensinya lebih lambat.
| Metode | Keuntungan | Kerugian |
|---|---|---|
| Biseksi | Konvergensi terjamin, sederhana | Konvergensi lambat |
| Newton-Raphson | Konvergensi cepat | Membutuhkan turunan pertama, tidak selalu konvergen |
Penggunaan Software Matematika
Software matematika seperti MATLAB, Mathematica, atau Python dengan library SciPy dapat digunakan untuk mencari akar persamaan secara efisien. Berikut contoh penggunaan SciPy di Python:
import numpy as npfrom scipy.optimize import fsolvedef f(x): return x3 - 2*x - 5akar = fsolve(f, 2) # 2 adalah tebakan awalprint(akar)
Kode di atas mendefinisikan fungsi f(x) dan kemudian menggunakan fungsi fsolve dari SciPy untuk mencari akarnya dengan tebakan awal 2. Hasilnya akan menampilkan nilai akar persamaan.
Kondisi Kesulitan Pencarian Akar
Beberapa kondisi dapat menyebabkan kesulitan dalam mencari akar persamaan. Kondisi tersebut antara lain:
- Fungsi yang memiliki banyak akar atau akar yang berdekatan.
- Fungsi yang memiliki turunan pertama yang bernilai nol atau mendekati nol di sekitar akar (untuk metode Newton-Raphson).
- Fungsi yang tidak kontinu atau tidak terdiferensialkan.
- Adanya error pembulatan dalam perhitungan numerik.
Aplikasi Akar Persamaan dalam Berbagai Bidang
Pencarian akar persamaan merupakan teknik matematis fundamental yang memiliki aplikasi luas di berbagai disiplin ilmu. Kemampuan untuk menemukan nilai variabel yang memenuhi suatu persamaan sangat krusial dalam memecahkan masalah kompleks di berbagai bidang, mulai dari rekayasa hingga ekonomi.
Penerapan Akar Persamaan dalam Teknik
Dalam dunia teknik, pencarian akar persamaan digunakan secara intensif untuk merancang dan menganalisis sistem. Proses ini memungkinkan insinyur untuk menemukan titik-titik kritis, titik kesetimbangan, atau solusi optimal untuk berbagai permasalahan.
- Desain Jembatan: Menentukan titik beban maksimum pada struktur jembatan melibatkan pencarian akar persamaan yang menggambarkan distribusi gaya dan tegangan pada jembatan tersebut. Dengan menemukan akar persamaan, insinyur dapat memastikan struktur jembatan mampu menahan beban yang direncanakan.
- Analisis Sirkuit Elektronik: Dalam analisis sirkuit, akar persamaan digunakan untuk menentukan arus dan tegangan pada berbagai titik dalam sirkuit. Menemukan akar persamaan yang menggambarkan hukum Kirchhoff memungkinkan perhitungan yang akurat untuk desain dan optimasi sirkuit.
- Perancangan Sistem Kontrol: Menentukan parameter kontrol optimal dalam sistem kontrol otomatis seringkali memerlukan pencarian akar persamaan karakteristik sistem. Akar-akar ini menentukan stabilitas dan respon sistem terhadap input.
Penggunaan Akar Persamaan dalam Pemodelan Matematika
Pemodelan matematika banyak mengandalkan persamaan untuk merepresentasikan fenomena alam atau sistem buatan manusia. Menemukan akar persamaan dalam model tersebut memungkinkan kita untuk memahami perilaku sistem dan memprediksi hasil di berbagai kondisi.
Contohnya, dalam pemodelan pertumbuhan populasi, persamaan diferensial digunakan untuk menggambarkan perubahan populasi dari waktu ke waktu. Menemukan akar persamaan yang terkait dapat membantu menentukan titik kesetimbangan populasi atau memprediksi pertumbuhan populasi di masa mendatang.
Penerapan Akar Persamaan dalam Ilmu Ekonomi
Dalam ilmu ekonomi, akar persamaan sering digunakan untuk menganalisis keseimbangan pasar, menentukan titik optimal produksi, atau memodelkan perilaku konsumen.
Sebagai contoh, menemukan titik keseimbangan pasar melibatkan pencarian akar persamaan permintaan dan penawaran. Titik potong antara kurva permintaan dan penawaran menunjukkan harga dan kuantitas keseimbangan di pasar.
Ilustrasi Penerapan Akar Persamaan dalam Fisika
Dalam fisika, akar persamaan berperan penting dalam memecahkan berbagai masalah, khususnya yang melibatkan gerak dan interaksi benda. Misalnya, dalam mekanika klasik, persamaan gerak suatu benda seringkali berupa persamaan diferensial orde dua. Menemukan akar persamaan karakteristik yang terkait memungkinkan kita untuk menentukan posisi dan kecepatan benda sebagai fungsi waktu.
Sebagai ilustrasi, perhatikan gerak peluru yang diluncurkan dengan sudut elevasi tertentu. Persamaan lintasan peluru dapat dimodelkan menggunakan persamaan parabola. Menemukan akar persamaan ini, yang merepresentasikan titik di mana peluru menyentuh tanah, memungkinkan kita untuk menentukan jangkauan peluru. Selain itu, analisis terhadap turunan persamaan lintasan (kecepatan) memungkinkan kita untuk menentukan waktu mencapai titik tertinggi dan kecepatan peluru pada titik tersebut.
Dengan demikian, pemahaman yang mendalam tentang akar persamaan sangat krusial untuk memahami dan memprediksi gerak peluru.
Contoh Masalah Nyata yang Solusinya Melibatkan Pencarian Akar Persamaan
Sebuah perusahaan manufaktur ingin menentukan jumlah produk yang harus diproduksi untuk memaksimalkan keuntungan. Keuntungan (P) dapat dimodelkan sebagai fungsi kuadrat dari jumlah produk (x): P(x) = -0.01x² + 10x – 500. Untuk menentukan jumlah produk (x) yang memaksimalkan keuntungan, kita perlu mencari akar persamaan turunan pertama dari fungsi keuntungan (dP/dx = 0), yang merupakan persamaan linear sederhana. Solusi persamaan ini memberikan jumlah produk yang menghasilkan keuntungan maksimum.
Interpretasi Akar Persamaan
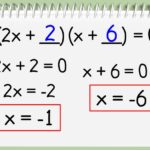
Menemukan akar-akar persamaan hanyalah setengah dari proses pemecahan masalah. Interpretasi yang tepat terhadap akar-akar tersebut sangat krusial untuk memahami makna solusi dalam konteks masalah nyata. Akar-akar persamaan tidak hanya sekadar angka, tetapi mewakili besaran fisik, kuantitas, atau variabel lain yang relevan dengan permasalahan yang dimodelkan dalam bentuk persamaan tersebut. Kemampuan menginterpretasikan akar-akar ini dengan tepat menentukan keberhasilan dalam penerapan matematika ke dunia nyata.
Interpretasi akar persamaan bergantung pada konteks permasalahan. Pemahaman yang mendalam tentang variabel-variabel yang terlibat dan satuannya sangat penting. Proses interpretasi ini seringkali melibatkan analisis dimensi, pemeriksaan realisme solusi, dan pertimbangan batasan-batasan fisik atau praktis.
Contoh Interpretasi Akar Persamaan
Misalnya, dalam persamaan kuadrat yang memodelkan lintasan proyektil, akar-akar persamaan mewakili waktu ketika proyektil mencapai tanah. Jika salah satu akar bernilai negatif, akar tersebut biasanya diabaikan karena waktu tidak dapat bernilai negatif dalam konteks ini. Akar positif menunjukkan waktu yang dibutuhkan proyektil untuk mencapai tanah setelah diluncurkan.
Sebagai contoh lain, perhatikan persamaan x²
-5x + 6 = 0 yang memiliki akar x = 2 dan x = 3. Jika persamaan ini merepresentasikan panjang sisi-sisi sebuah persegi panjang dengan luas 6 satuan luas dan keliling 10 satuan luas, maka akar-akarnya merepresentasikan panjang kedua sisi persegi panjang tersebut, yaitu 2 dan 3 satuan luas.
Interpretasi Ganda dan Implikasinya
Dalam beberapa kasus, akar persamaan dapat memiliki lebih dari satu interpretasi yang masuk akal. Hal ini dapat terjadi jika variabel dalam persamaan mewakili lebih dari satu besaran fisik atau konsep. Ambil contoh persamaan yang menggambarkan kecepatan suatu objek. Akar positif dapat mewakili kecepatan ke arah tertentu, sedangkan akar negatif dapat mewakili kecepatan ke arah yang berlawanan. Interpretasi yang tepat bergantung pada konteks dan definisi arah yang digunakan.
Interpretasi Akar Persamaan dalam Pengambilan Keputusan
Interpretasi akar persamaan sangat penting dalam berbagai bidang pengambilan keputusan. Misalnya, dalam rekayasa, akar persamaan dapat mewakili tegangan kritis pada suatu struktur. Interpretasi yang salah terhadap akar-akar tersebut dapat menyebabkan kesalahan perencanaan yang berakibat fatal. Dalam bidang ekonomi, akar persamaan dapat mewakili titik keseimbangan pasar. Interpretasi yang tepat terhadap akar-akar ini sangat penting untuk menentukan strategi bisnis yang efektif.
Akar Persamaan yang Tidak Relevan
Tidak semua akar persamaan selalu relevan atau masuk akal dalam konteks permasalahan. Misalnya, dalam persamaan yang memodelkan populasi, akar negatif tidak relevan karena populasi tidak dapat bernilai negatif. Demikian pula, akar yang menghasilkan nilai yang jauh melebihi batas-batas yang realistis juga perlu dipertimbangkan kembali. Proses verifikasi dan validasi solusi sangat penting untuk memastikan bahwa akar-akar yang dipilih sesuai dengan konteks masalah.
Ringkasan Akhir
Mencari akar persamaan bukan hanya sekadar menyelesaikan persamaan matematika; ini adalah kunci untuk memahami dan memodelkan dunia di sekitar kita. Dengan memahami berbagai metode dan implikasinya, kita dapat mengatasi berbagai tantangan dalam sains, teknik, dan ekonomi. Kemampuan untuk menginterpretasikan arti fisik dari akar-akar persamaan juga sangat penting dalam pengambilan keputusan yang tepat dan efektif.
Semoga pemahaman yang lebih mendalam tentang akar persamaan ini memberikan wawasan baru dan memudahkan dalam menghadapi permasalahan yang lebih kompleks di masa mendatang.