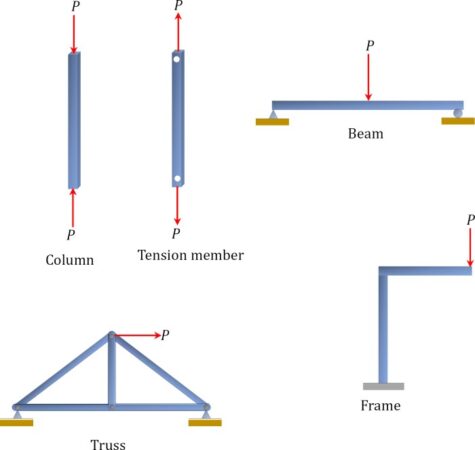
Analisis struktur merupakan studi penting untuk memahami bagaimana suatu sistem, baik fisik maupun abstrak, tersusun dan berinteraksi. Memahami analisis struktur memungkinkan kita untuk memprediksi perilaku sistem tersebut di bawah berbagai kondisi. Dari bangunan pencakar langit hingga algoritma komputer yang kompleks, analisis struktur memberikan landasan bagi desain, optimasi, dan pemeliharaan sistem yang handal dan efisien. Kajian ini akan menelusuri berbagai metode, teknik, dan penerapan analisis struktur secara komprehensif.
Topik ini akan membahas berbagai jenis struktur data yang digunakan dalam analisis struktur, menjelaskan metode analisis yang berbeda, cara menginterpretasikan hasil analisis, serta berbagai penerapannya di berbagai bidang. Dengan pemahaman yang komprehensif, kita akan mampu mengaplikasikan prinsip-prinsip analisis struktur dalam memecahkan masalah nyata.
Pengantar Struktur Data: Analisis Struktur
Analisis struktur, baik dalam bidang teknik sipil, ilmu komputer, maupun ilmu lainnya, sangat bergantung pada representasi data yang efisien dan terstruktur. Pemilihan struktur data yang tepat akan secara signifikan memengaruhi efisiensi dan kompleksitas algoritma yang digunakan dalam analisis. Pemahaman mendalam tentang berbagai jenis struktur data dan karakteristiknya merupakan kunci keberhasilan dalam analisis struktur yang kompleks.
Berbagai jenis struktur data digunakan dalam analisis struktur, masing-masing dengan kelebihan dan kekurangannya sendiri. Pilihan struktur data yang tepat bergantung pada jenis masalah yang dihadapi dan karakteristik data yang akan diproses.
Jenis-jenis Struktur Data dalam Analisis Struktur
Beberapa struktur data yang umum digunakan dalam analisis struktur meliputi array, linked list, tree (pohon), graph (graf), dan hash table. Setiap struktur ini memiliki karakteristik unik yang membuatnya cocok untuk tugas analisis tertentu.
- Array: Struktur data sederhana yang menyimpan elemen-elemen data dalam urutan berurutan. Dalam analisis struktur, array dapat digunakan untuk menyimpan data nodal seperti koordinat titik-titik pada struktur. Kelebihannya adalah akses elemen yang cepat, namun ukurannya tetap dan kurang fleksibel untuk operasi penyisipan atau penghapusan elemen.
- Linked List: Struktur data yang menyimpan elemen-elemen data dalam bentuk node yang saling terhubung. Linked list lebih fleksibel daripada array karena memungkinkan penyisipan dan penghapusan elemen dengan mudah. Dalam analisis struktur, linked list dapat digunakan untuk merepresentasikan elemen-elemen struktur yang terhubung, misalnya untuk menyimpan informasi elemen-elemen balok dalam struktur rangka.
- Tree (Pohon): Struktur data hierarkis yang terdiri dari node dan cabang. Dalam analisis struktur, pohon dapat digunakan untuk merepresentasikan hierarki elemen struktur, misalnya dalam analisis elemen hingga (finite element analysis). Pohon pencarian biner (binary search tree) dapat digunakan untuk pencarian data yang efisien.
- Graph (Graf): Struktur data yang terdiri dari node (simpul) dan edge (sisi) yang menghubungkan node-node tersebut. Graf digunakan untuk merepresentasikan hubungan antar elemen struktur, misalnya dalam analisis jaringan struktur.
- Hash Table: Struktur data yang menggunakan fungsi hash untuk memetakan kunci ke indeks dalam array. Hash table sangat efisien untuk pencarian, penyisipan, dan penghapusan elemen, jika fungsi hash yang tepat digunakan. Dalam analisis struktur, hash table dapat digunakan untuk menyimpan dan mengakses data material dengan cepat berdasarkan propertinya.
Perbandingan Struktur Data
Tabel berikut membandingkan tiga struktur data yang paling umum digunakan dalam analisis struktur: array, linked list, dan pohon biner.
| Struktur Data | Kompleksitas Waktu (Pencarian) | Kompleksitas Ruang | Kegunaan |
|---|---|---|---|
| Array | O(n) | O(n) | Penyimpanan data nodal, data material |
| Linked List | O(n) | O(n) | Representasi elemen struktur terhubung |
| Pohon Biner | O(log n) (rata-rata), O(n) (terburuk) | O(n) | Representasi hierarki elemen struktur, pencarian data efisien |
Ilustrasi Penggunaan Struktur Pohon dalam Analisis Struktur
Bayangkan sebuah struktur rangka sederhana berupa segitiga. Struktur pohon dapat merepresentasikan struktur ini dengan node akar yang mewakili seluruh struktur. Tiga node cabang dari akar mewakili tiga balok yang membentuk segitiga. Setiap node balok dapat memiliki node cabang lebih lanjut untuk mewakili titik-titik sambungan (node) pada balok tersebut. Cabang-cabang mewakili hubungan antara elemen-elemen struktur.
Dengan demikian, struktur pohon memberikan representasi hierarkis yang jelas dan terstruktur dari elemen-elemen dan hubungannya dalam analisis struktur.
Sebagai contoh lebih detail, node akar dapat mewakili seluruh struktur rangka. Kemudian, tiga node cabang dari akar mewakili masing-masing balok. Setiap node balok akan memiliki dua node cabang lagi yang mewakili kedua ujung balok (node struktur). Dengan cara ini, kita dapat merepresentasikan seluruh struktur rangka dan hubungan antar elemennya secara hierarkis. Informasi seperti panjang balok, material, dan gaya yang bekerja pada balok dapat disimpan pada masing-masing node balok.
Metode Analisis Struktur

Analisis struktur merupakan proses penting dalam rekayasa dan ilmu pengetahuan untuk memahami perilaku suatu struktur di bawah beban. Pemahaman ini krusial untuk memastikan keamanan dan ketahanan struktur. Terdapat beberapa metode analisis yang dapat digunakan, masing-masing dengan kelebihan dan kekurangannya sendiri. Berikut ini akan dijelaskan tiga metode analisis struktur yang umum digunakan, beserta langkah-langkahnya dan perbandingan antar metode.
Metode Analisis Kekakuan Langsung (Direct Stiffness Method)
Metode kekakuan langsung merupakan metode matriks yang sangat populer dalam analisis struktur. Prinsip dasar metode ini adalah membangun matriks kekakuan global struktur dari matriks kekakuan elemen individual. Metode ini efektif untuk menganalisis struktur yang kompleks dengan banyak elemen.
- Pembentukan elemen-elemen struktur: Struktur dibagi menjadi beberapa elemen sederhana (batang, balok, dll).
- Penentuan matriks kekakuan elemen: Matriks kekakuan dihitung untuk setiap elemen berdasarkan sifat material dan geometri elemen.
- Asembli matriks kekakuan global: Matriks kekakuan elemen dikombinasikan untuk membentuk matriks kekakuan global struktur.
- Penerapan kondisi batas: Kondisi batas (seperti dukungan dan beban) diterapkan pada matriks kekakuan global.
- Penyelesaian persamaan keseimbangan: Sistem persamaan linier diselesaikan untuk mendapatkan perpindahan pada setiap titik simpul struktur.
- Penentuan tegangan dan gaya dalam elemen: Setelah perpindahan diketahui, tegangan dan gaya dalam setiap elemen dapat dihitung.
Metode Elemen Hingga (Finite Element Method)
Metode elemen hingga merupakan generalisasi dari metode kekakuan langsung. Metode ini memungkinkan analisis struktur dengan geometri yang lebih kompleks dan beban yang lebih beragam. Prinsip utamanya adalah membagi struktur menjadi sejumlah elemen kecil (elemen hingga) dan menyelesaikan persamaan keseimbangan pada setiap elemen.
- Diskritisasi: Struktur dibagi menjadi sejumlah elemen hingga dengan bentuk dan ukuran yang bervariasi sesuai dengan kompleksitas geometri.
- Pemilihan fungsi interpolasi: Fungsi interpolasi digunakan untuk menggambarkan variasi perpindahan di dalam setiap elemen.
- Formulasi elemen: Persamaan keseimbangan dan konstitutif dirumuskan untuk setiap elemen.
- Asembli: Persamaan elemen digabungkan untuk membentuk sistem persamaan global.
- Penyelesaian: Sistem persamaan diselesaikan secara numerik untuk mendapatkan perpindahan pada titik-titik simpul.
- Post-processing: Tegangan dan gaya dalam setiap elemen dihitung berdasarkan perpindahan yang telah diperoleh.
Metode Matriks Kekakuan
Metode matriks kekakuan merupakan pendekatan sistematis untuk analisis struktur. Prinsip dasarnya adalah merepresentasikan struktur dan bebannya dalam bentuk persamaan matriks. Metode ini efektif untuk analisis struktur rangka.
- Menentukan derajat kebebasan struktur.
- Membentuk matriks kekakuan global.
- Menentukan vektor beban.
- Memecahkan persamaan keseimbangan (K*U = F), dimana K adalah matriks kekakuan, U adalah vektor perpindahan, dan F adalah vektor beban.
- Menghitung tegangan dan gaya dalam elemen.
Perbandingan Metode Analisis Struktur
| Metode | Kelebihan | Kekurangan |
|---|---|---|
| Kekakuan Langsung | Relatif sederhana untuk struktur sederhana | Kompleksitas meningkat secara signifikan untuk struktur yang kompleks |
| Elemen Hingga | Dapat menangani geometri dan beban yang kompleks | Membutuhkan perangkat lunak dan komputasi yang lebih canggih |
| Matriks Kekakuan | Sistematis dan efisien untuk struktur rangka | Kurang fleksibel untuk geometri yang kompleks |
Penerapan Metode Kekakuan Langsung pada Contoh Kasus Sederhana
Berikut contoh penerapan metode kekakuan langsung pada balok sederhana:
Contoh Kasus: Sebuah balok sederhana dengan panjang 10 meter, modulus elastisitas 200 GPa, dan luas penampang 0.1 m2, ditahan pada kedua ujungnya dan diberi beban terpusat 10 kN di tengah.Langkah 1: Membagi balok menjadi dua elemen.Langkah 2: Menghitung matriks kekakuan untuk setiap elemen.Langkah 3: Merakit matriks kekakuan global.Langkah 4: Menerapkan kondisi batas.Langkah 5: Memecahkan persamaan untuk mendapatkan perpindahan.Langkah 6: Menghitung tegangan dan gaya dalam setiap elemen.
Diagram Alur Metode Kekakuan Langsung
Diagram alur berikut menggambarkan langkah-langkah dalam metode kekakuan langsung:
Mula → Pembentukan Elemen → Penentuan Matriks Kekakuan Elemen → Asembli Matriks Kekakuan Global → Penerapan Kondisi Batas → Penyelesaian Persamaan Keseimbangan → Penentuan Tegangan dan Gaya Dalam Elemen → Selesai
Interpretasi Hasil Analisis
Interpretasi hasil analisis struktur merupakan langkah krusial dalam memahami perilaku dan kinerja suatu struktur. Tahap ini melibatkan penilaian kritis terhadap data yang diperoleh dari analisis, menghubungkan data tersebut dengan kondisi aktual struktur, dan menarik kesimpulan yang bermakna. Kemampuan menginterpretasi hasil dengan tepat akan menentukan efektifitas desain dan tindakan perbaikan yang diambil.
Proses interpretasi ini tidak hanya bergantung pada angka-angka yang dihasilkan oleh software analisis, tetapi juga pada pemahaman mendalam tentang prinsip-prinsip rekayasa struktur, jenis beban yang bekerja, dan material yang digunakan. Kesalahan interpretasi dapat berujung pada keputusan desain yang salah dan berpotensi menimbulkan bahaya.
Contoh Interpretasi Hasil Analisis Struktur Berbagai Skenario
Interpretasi hasil analisis bervariasi tergantung pada jenis analisis yang dilakukan (misalnya, analisis statis linier, analisis dinamik, analisis non-linier) dan tujuan analisis tersebut. Berikut beberapa contoh:
- Analisis Statis Linier Balok Sederhana: Jika analisis menunjukkan tegangan lentur maksimum pada balok melebihi kekuatan luluh material, hal ini mengindikasikan balok tersebut tidak aman dan perlu didesain ulang dengan dimensi yang lebih besar atau material yang lebih kuat.
- Analisis Dinamik Gedung Tinggi: Hasil analisis mungkin menunjukkan frekuensi alami gedung dan responnya terhadap beban gempa. Jika frekuensi alami gedung berdekatan dengan frekuensi gempa yang dominan, hal ini mengindikasikan potensi resonansi dan perlu dilakukan pertimbangan khusus dalam desain untuk mengurangi respon tersebut, misalnya dengan menggunakan peredam getaran.
- Analisis Non-Linier Struktur Beton Bertulang: Hasil analisis dapat menunjukkan retak pada beton dan perilaku plastis pada tulangan. Interpretasi hasil ini memerlukan pemahaman mendalam tentang perilaku material beton dan tulangan di bawah beban, untuk memastikan struktur tetap memenuhi persyaratan keamanan.
Panduan Langkah Demi Langkah Interpretasi Hasil Analisis Struktur
Berikut panduan langkah demi langkah untuk interpretasi yang akurat:
- Verifikasi Model: Pastikan model analisis merepresentasikan struktur aktual secara akurat, termasuk geometri, material, dan kondisi penyangga.
- Review Asumsi Analisis: Pahami asumsi yang digunakan dalam analisis (misalnya, linieritas, elastisitas) dan batasannya. Pertimbangkan apakah asumsi tersebut sesuai dengan kondisi aktual.
- Analisis Tegangan dan Deformasi: Identifikasi lokasi tegangan dan deformasi maksimum. Bandingkan nilai-nilai tersebut dengan kapasitas material dan batasan desain yang berlaku.
- Evaluasi Stabilitas: Periksa stabilitas struktur secara keseluruhan, memastikan tidak terjadi keruntuhan atau mekanisme keruntuhan yang tidak terduga.
- Verifikasi Hasil dengan Standar dan Regulasi: Pastikan hasil analisis memenuhi persyaratan standar dan regulasi desain yang berlaku.
Potensi Kesalahan Interpretasi dan Cara Mengatasinya
Beberapa kesalahan umum dalam interpretasi hasil analisis meliputi:
- Salah Interpretasi Nilai Tegangan: Mengabaikan pengaruh faktor keamanan atau mengabaikan perbedaan antara tegangan nominal dan tegangan aktual.
- Mengabaikan Efek Non-Linier: Menggunakan hasil analisis linier untuk struktur yang berperilaku non-linier.
- Kurang Memahami Batasan Analisis: Tidak memperhatikan asumsi dan batasan yang digunakan dalam analisis.
Untuk mengatasi kesalahan ini, diperlukan pemahaman yang mendalam tentang prinsip-prinsip analisis struktur, penggunaan software analisis yang tepat, dan review kritis terhadap hasil analisis oleh ahli struktur yang berpengalaman.
Poin Penting dalam Interpretasi Hasil Analisis Struktur
Berikut poin-poin penting yang perlu diperhatikan:
- Konteks desain dan tujuan analisis.
- Jenis beban dan kondisi pembebanan.
- Sifat material dan perilaku material non-linier.
- Keadaan batas dan kondisi penyangga.
- Standar dan regulasi desain yang berlaku.
Penerapan Analisis Struktur
Analisis struktur, sebagai disiplin ilmu yang mempelajari perilaku struktur di bawah beban, memiliki penerapan yang luas dan vital dalam berbagai bidang. Pemahaman mendalam tentang prinsip-prinsip analisis struktur memungkinkan perancangan struktur yang aman, efisien, dan ekonomis. Berikut beberapa contoh penerapannya dan perbandingan antar bidang.
Analisis Struktur dalam Rekayasa Sipil
Di bidang rekayasa sipil, analisis struktur merupakan fondasi utama dalam perancangan bangunan, jembatan, bendungan, dan infrastruktur lainnya. Analisis ini memungkinkan insinyur untuk memprediksi tegangan, regangan, dan defleksi pada struktur di bawah berbagai kondisi pembebanan, memastikan keamanan dan ketahanan struktur terhadap beban statis dan dinamis. Misalnya, dalam perancangan gedung pencakar langit, analisis struktur yang rinci dibutuhkan untuk memperhitungkan beban angin, gempa bumi, dan beban mati bangunan agar gedung tersebut dapat berdiri kokoh dan aman.
Analisis Struktur dalam Rekayasa Mesin
Dalam rekayasa mesin, analisis struktur digunakan untuk mendesain komponen mesin seperti poros, balok, dan rangka yang mampu menahan beban kerja dan beroperasi secara efisien. Teknik seperti analisis elemen hingga (FEA) digunakan secara ekstensif untuk memodelkan dan menganalisis perilaku komponen mesin di bawah berbagai kondisi operasi. Misalnya, analisis struktur pada poros mesin memastikan bahwa poros mampu menahan torsi dan beban lentur tanpa mengalami kerusakan atau patah.
Perbandingan Penerapan Analisis Struktur
Meskipun prinsip-prinsip dasar analisis struktur sama di kedua bidang, penerapannya berbeda dalam hal jenis beban, material yang digunakan, dan kompleksitas struktur. Rekayasa sipil seringkali menangani struktur berskala besar dengan beban statis dan dinamis yang kompleks, sementara rekayasa mesin berfokus pada komponen berskala lebih kecil dengan beban yang relatif lebih sederhana. Namun, keduanya sama-sama mengandalkan prinsip-prinsip mekanika material dan persamaan keseimbangan untuk memastikan keamanan dan kinerja struktur.
Studi Kasus: Perancangan Jembatan Menggunakan Analisis Struktur
Penerapan analisis struktur secara efektif telah terbukti dalam banyak proyek infrastruktur. Sebagai contoh, perancangan Jembatan Suramadu di Indonesia, yang merupakan jembatan terpanjang di Indonesia, mengandalkan analisis struktur yang intensif. Analisis ini memperhitungkan berbagai faktor seperti beban lalu lintas, beban angin, dan beban gempa bumi.
- Analisis struktur memastikan jembatan mampu menahan beban yang signifikan tanpa mengalami deformasi atau kerusakan yang signifikan.
- Simulasi numerik menggunakan perangkat lunak analisis elemen hingga membantu dalam mengoptimalkan desain jembatan dan meminimalkan biaya konstruksi.
- Penggunaan material yang tepat dan desain yang optimal, yang didasarkan pada hasil analisis struktur, memastikan ketahanan dan umur pakai jembatan yang panjang.
Tantangan dan Kendala dalam Penerapan Analisis Struktur
Meskipun analisis struktur merupakan alat yang sangat berharga, beberapa tantangan dan kendala dapat dihadapi dalam penerapannya. Kompleksitas geometri struktur, perilaku material yang non-linear, dan ketidakpastian dalam beban yang bekerja pada struktur dapat menyulitkan proses analisis. Selain itu, keterbatasan komputasi dan keakuratan model numerik juga dapat memengaruhi hasil analisis. Penting untuk diingat bahwa analisis struktur hanyalah alat bantu, dan keahlian dan pengalaman insinyur tetap menjadi faktor kunci dalam memastikan keamanan dan keandalan struktur.
Kesimpulan Akhir
Kesimpulannya, analisis struktur merupakan disiplin ilmu yang krusial dalam berbagai bidang, mulai dari rekayasa sipil hingga ilmu komputer. Dengan memahami berbagai metode analisis, struktur data yang tepat, dan interpretasi hasil yang akurat, kita dapat membangun sistem yang lebih handal, efisien, dan tahan lama. Penguasaan analisis struktur membuka peluang untuk inovasi dan pemecahan masalah yang lebih efektif di masa depan.