Bentuk pangkat merupakan konsep dasar matematika yang sangat penting. Mempelajari bentuk pangkat bukan hanya sekadar memahami perkalian berulang, tetapi juga membuka pintu untuk memahami berbagai fenomena di sekitar kita. Dari perhitungan bunga majemuk hingga pertumbuhan populasi, bentuk pangkat berperan krusial. Dalam uraian berikut, kita akan menjelajahi definisi, sifat-sifat, penerapan, dan penyederhanaan bentuk pangkat, termasuk hubungannya dengan bentuk akar.
Kita akan mulai dengan definisi matematis bentuk pangkat, kemudian mengkaji sifat-sifatnya dalam operasi hitung seperti perkalian, pembagian, dan perpangkatan. Selanjutnya, akan dibahas penerapannya dalam berbagai konteks, termasuk ilmu fisika, komputer, dan keuangan. Penyederhanaan bentuk pangkat yang melibatkan basis dan eksponen kompleks juga akan dijelaskan secara detail, termasuk hubungannya dengan bentuk akar dan cara konversinya.
Pengertian Bentuk Pangkat
Bentuk pangkat merupakan suatu konsep matematika yang menyatakan perkalian berulang dari suatu bilangan. Konsep ini sangat fundamental dan diterapkan luas dalam berbagai bidang, mulai dari aljabar hingga kalkulus. Memahami bentuk pangkat dan sifat-sifatnya sangat penting untuk menguasai matematika lebih lanjut.
Secara matematis, bentuk pangkat didefinisikan sebagai an, di mana ‘a’ disebut basis (bilangan pokok) dan ‘n’ disebut eksponen (pangkat). Eksponen menunjukkan berapa kali basis dikalikan dengan dirinya sendiri. Misalnya, 2 3 berarti 2 × 2 × 2 = 8.
Contoh Bentuk Pangkat
Berikut beberapa contoh bentuk pangkat dengan basis dan eksponen yang berbeda:
- 3 4 = 3 × 3 × 3 × 3 = 81
- 5 2 = 5 × 5 = 25
- 10 6 = 10 × 10 × 10 × 10 × 10 × 10 = 1.000.000
- (1/2) 3 = (1/2) × (1/2) × (1/2) = 1/8
- (-2) 4 = (-2) × (-2) × (-2) × (-2) = 16
Perbedaan Pangkat Positif, Negatif, dan Nol
Pangkat positif, negatif, dan nol memiliki arti dan sifat yang berbeda. Memahami perbedaan ini krusial dalam perhitungan matematika.
Pangkat Positif: Menunjukkan perkalian berulang basis sebanyak eksponen. Contoh: 2 3 = 8
Pangkat Negatif: Menunjukkan kebalikan dari pangkat positif. a-n = 1/a n. Contoh: 2 -3 = 1/2 3 = 1/8
Pangkat Nol: Setiap bilangan (kecuali nol) yang dipangkatkan nol hasilnya selalu
1. a0 = 1 (dengan a ≠ 0). Contoh: 5 0 = 1
Tabel Perbandingan Sifat Pangkat
Tabel berikut merangkum perbedaan sifat-sifat pangkat positif, negatif, dan nol:
| Sifat | Pangkat Positif | Pangkat Negatif | Pangkat Nol |
|---|---|---|---|
| Definisi | Perkalian berulang basis | Kebalikan dari pangkat positif | Selalu bernilai 1 (jika basis ≠ 0) |
| Contoh | 23 = 8 | 2-3 = 1/8 | 20 = 1 |
| Hasil | Bilangan positif atau negatif tergantung basis | Bilangan positif atau negatif tergantung basis | Selalu 1 |
Aturan Operasi Hitung Bentuk Pangkat
Beberapa aturan dasar operasi hitung pada bentuk pangkat meliputi perkalian, pembagian, dan perpangkatan.
- Perkalian: am × a n = a m+n. Basis harus sama untuk dapat dikalikan.
- Pembagian: am / a n = a m-n. Basis harus sama untuk dapat dibagi.
- Perpangkatan: (am) n = a m×n
Pemahaman aturan-aturan ini sangat penting untuk menyederhanakan dan menyelesaikan soal-soal yang melibatkan bentuk pangkat.
Sifat-Sifat Bentuk Pangkat
Bentuk pangkat merupakan cara singkat untuk menulis perkalian berulang suatu bilangan. Memahami sifat-sifat bentuk pangkat sangat penting dalam berbagai bidang, mulai dari aljabar hingga kalkulus. Pemahaman yang baik akan sifat-sifat ini akan memudahkan penyelesaian berbagai permasalahan matematika yang melibatkan pangkat.
Perkalian Bentuk Pangkat dengan Basis yang Sama
Ketika mengalikan dua bentuk pangkat dengan basis yang sama, kita dapat menjumlahkan eksponennya. Hal ini berlaku karena perkalian berulang tersebut dapat digabungkan menjadi satu perkalian yang lebih besar. Secara matematis, sifat ini dapat dituliskan sebagai berikut:
am × a n = a m+n
Berikut beberapa contoh soal dan penyelesaiannya:
- Soal: Hitunglah 2 3 × 2 4
- Penyelesaian: 2 3 × 2 4 = 2 3+4 = 2 7 = 128
- Soal: Sederhanakan x 5 × x 2
- Penyelesaian: x 5 × x 2 = x 5+2 = x 7
- Soal: Tentukan hasil dari (-3) 2 × (-3) 3
- Penyelesaian: (-3) 2 × (-3) 3 = (-3) 2+3 = (-3) 5 = -243
Pembagian Bentuk Pangkat dengan Basis yang Sama
Berbeda dengan perkalian, ketika membagi dua bentuk pangkat dengan basis yang sama, kita dapat mengurangkan eksponennya. Konsep ini merupakan kebalikan dari sifat perkalian pangkat. Rumusnya adalah:
am ÷ a n = a m-n (dengan syarat a ≠ 0)
Berikut beberapa contoh soal dan penyelesaiannya:
- Soal: Hitunglah 5 6 ÷ 5 2
- Penyelesaian: 5 6 ÷ 5 2 = 5 6-2 = 5 4 = 625
- Soal: Sederhanakan y 8 ÷ y 3
- Penyelesaian: y 8 ÷ y 3 = y 8-3 = y 5
- Soal: Tentukan hasil dari (-4) 5 ÷ (-4) 2
- Penyelesaian: (-4) 5 ÷ (-4) 2 = (-4) 5-2 = (-4) 3 = -64
Perpangkatan Bentuk Pangkat
Jika kita memangkatkan suatu bentuk pangkat, kita dapat mengalikan eksponennya. Sifat ini memperlihatkan bagaimana perkalian berulang dari pangkat dapat disederhanakan. Rumusnya adalah:
(am) n = a m×n
Berikut beberapa contoh soal dan penyelesaiannya:
- Soal: Hitunglah (3 2) 3
- Penyelesaian: (3 2) 3 = 3 2×3 = 3 6 = 729
- Soal: Sederhanakan (x 4) 2
- Penyelesaian: (x 4) 2 = x 4×2 = x 8
- Soal: Tentukan hasil dari ((-2) 3) 2
- Penyelesaian: ((-2) 3) 2 = (-2) 3×2 = (-2) 6 = 64
Contoh Soal Gabungan Sifat Bentuk Pangkat
Berikut contoh soal yang menggabungkan beberapa sifat bentuk pangkat:
- Soal: Sederhanakan (2 3 × 2 2) 2 ÷ 2 4
- Penyelesaian: (2 3 × 2 2) 2 ÷ 2 4 = (2 3+2) 2 ÷ 2 4 = (2 5) 2 ÷ 2 4 = 2 10 ÷ 2 4 = 2 10-4 = 2 6 = 64
- Soal: Hitunglah (x 4y 2) 3 ÷ (x 2y) 2
- Penyelesaian: (x 4y 2) 3 ÷ (x 2y) 2 = (x 12y 6) ÷ (x 4y 2) = x 12-4y 6-2 = x 8y 4
Penerapan Bentuk Pangkat dalam Berbagai Konteks
Bentuk pangkat, atau eksponen, merupakan konsep matematika fundamental yang memiliki penerapan luas di berbagai disiplin ilmu. Pemahaman yang mendalam tentang bentuk pangkat memungkinkan kita untuk menyelesaikan permasalahan kompleks dengan lebih efisien dan akurat, mulai dari perhitungan sederhana hingga model-model ilmiah yang rumit.
Penerapan Bentuk Pangkat dalam Ilmu Fisika
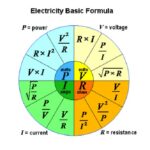
Bentuk pangkat sering digunakan dalam rumus-rumus fisika untuk menggambarkan hubungan kuantitatif antara besaran-besaran fisika. Salah satu contoh yang paling umum adalah rumus energi kinetik, yang menyatakan bahwa energi kinetik (Ek) suatu benda bermassa (m) yang bergerak dengan kecepatan (v) dihitung dengan rumus Ek = ½mv². Di sini, kecepatan (v) dipangkatkan dua, menunjukkan bahwa energi kinetik berbanding lurus dengan kuadrat kecepatan.
Semakin tinggi kecepatan, semakin besar pula energi kinetiknya, dan hubungannya bersifat kuadratik, bukan linier.
Penerapan Bentuk Pangkat dalam Ilmu Komputer
Dalam ilmu komputer, bentuk pangkat berperan penting dalam representasi data biner. Sistem bilangan biner menggunakan basis 2, di mana setiap digit mewakili pangkat dari 2. Misalnya, bilangan desimal 13 dapat direpresentasikan dalam biner sebagai 1101, yang setara dengan (1 x 2³) + (1 x 2²) + (0 x 2¹) + (1 x 2⁰) = 8 + 4 + 0 + 1 = 13.
Konsep pangkat dua juga mendasari algoritma dan struktur data tertentu, seperti pencarian biner dan pohon biner.
Penerapan Bentuk Pangkat dalam Bidang Keuangan
Perhitungan bunga majemuk merupakan contoh penerapan bentuk pangkat dalam bidang keuangan. Rumus bunga majemuk melibatkan pangkat untuk menghitung nilai investasi setelah periode waktu tertentu. Misalnya, jika modal awal (P) diinvestasikan dengan suku bunga tahunan (r) selama (t) tahun, nilai akhir (A) dapat dihitung dengan rumus A = P(1 + r) t. Pangkat (t) menunjukkan bahwa nilai investasi meningkat secara eksponensial seiring berjalannya waktu.
Penerapan Bentuk Pangkat dalam Pertumbuhan Populasi
Model pertumbuhan eksponensial sering digunakan untuk memprediksi pertumbuhan populasi. Model ini mengasumsikan bahwa laju pertumbuhan populasi konstan, sehingga populasi meningkat secara eksponensial seiring waktu. Rumus pertumbuhan eksponensial dapat ditulis sebagai P(t) = P₀e rt, di mana P(t) adalah populasi pada waktu t, P₀ adalah populasi awal, r adalah laju pertumbuhan, dan e adalah konstanta Euler (sekitar 2.718). Rumus ini menunjukkan bagaimana pangkat (rt) mempengaruhi pertumbuhan populasi secara signifikan.
Memahami bentuk pangkat sangat penting dalam berbagai disiplin ilmu karena memungkinkan kita untuk memodelkan dan menganalisis fenomena alam dan sosial yang kompleks. Kemampuan untuk memahami dan memanipulasi bentuk pangkat merupakan kunci untuk memecahkan masalah dalam fisika, komputer, keuangan, biologi, dan banyak bidang lainnya.
Penyederhanaan Bentuk Pangkat
Penyederhanaan bentuk pangkat merupakan keterampilan penting dalam aljabar. Memahami aturan-aturan dasar penyederhanaan akan memudahkan kita dalam menyelesaikan berbagai persamaan dan soal matematika yang lebih kompleks. Proses ini melibatkan penerapan sifat-sifat pangkat untuk menyederhanakan ekspresi yang mengandung pangkat, sehingga menghasilkan bentuk yang lebih ringkas dan mudah dipahami.
Penyederhanaan Bentuk Pangkat dengan Perkalian dan Pembagian
Penyederhanaan bentuk pangkat yang melibatkan perkalian dan pembagian didasarkan pada sifat-sifat perkalian dan pembagian pangkat dengan basis yang sama. Pada perkalian, eksponen dijumlahkan, sedangkan pada pembagian, eksponen dikurangkan.
- Contoh 1 (Perkalian): 2 3 x 2 2 = 2 (3+2) = 2 5 = 32
- Contoh 2 (Pembagian): 5 6 / 5 2 = 5 (6-2) = 5 4 = 625
Dalam contoh di atas, terlihat bagaimana sifat-sifat perkalian dan pembagian pangkat diterapkan untuk mendapatkan bentuk yang lebih sederhana.
Penyederhanaan Bentuk Pangkat dengan Perpangkatan
Jika suatu bentuk pangkat dipangkatkan lagi, maka eksponennya dikalikan. Ini merupakan sifat perpangkatan yang sering digunakan dalam penyederhanaan bentuk pangkat yang lebih kompleks.
- Contoh: (3 2) 3 = 3 (2×3) = 3 6 = 729
Proses ini melibatkan perkalian eksponen luar dengan eksponen dalam. Hasilnya merupakan bentuk pangkat yang lebih sederhana.
Penyederhanaan Bentuk Pangkat dengan Basis dan Eksponen Kompleks
Penyederhanaan bentuk pangkat dapat melibatkan basis dan eksponen yang lebih kompleks. Dalam kasus ini, perlu pemahaman yang lebih mendalam tentang sifat-sifat pangkat dan aturan-aturan aljabar.
Contoh: Sederhanakan (2x 2y 3) 4 / (4x 3y) 2
- Pangkatkan setiap faktor dalam kurung: (16x8y 12) / (16x 6y 2)
- Sederhanakan dengan mengurangi eksponen basis yang sama: x (8-6)y (12-2) = x 2y 10
- Hasil penyederhanaan: x 2y 10
Ilustrasi Penyederhanaan Bentuk Pangkat (am)n = a(m*n)
Ilustrasi ini menjelaskan bagaimana perpangkatan pangkat bekerja. Misalnya, (a m) n berarti kita mengalikan a m sebanyak n kali. Jika kita menuliskan a m sebanyak n kali dan mengalikannya, kita akan mendapatkan a dikalikan sebanyak m x n kali, sehingga hasilnya adalah a (m*n).
Sebagai contoh konkret, bayangkan (2 3) 2. Ini berarti (2 3) x (2 3) = (2 x 2 x 2) x (2 x 2 x 2) = 2 6. Perhatikan bahwa 3 x 2 = 6, sehingga kita mendapatkan rumus (a m) n = a (m*n). Rumus ini memperlihatkan bahwa perpangkatan berulang dapat disederhanakan dengan mengalikan eksponennya.
Bentuk Akar dan Hubungannya dengan Bentuk Pangkat
Bentuk akar dan bentuk pangkat merupakan dua representasi matematika yang saling berkaitan erat. Memahami hubungan keduanya sangat penting untuk menyederhanakan ekspresi matematika dan menyelesaikan berbagai persamaan. Pada dasarnya, bentuk akar dapat diubah menjadi bentuk pangkat dan sebaliknya, memudahkan manipulasi aljabar yang lebih kompleks.
Hubungan fundamental antara bentuk akar dan bentuk pangkat terletak pada definisi masing-masing. Bentuk akar, misalnya √a, menyatakan bilangan yang jika dipangkatkan dua akan menghasilkan a. Sedangkan bentuk pangkat, a n, menyatakan perkalian berulang dari bilangan a sebanyak n kali. Dengan memahami definisi ini, kita dapat dengan mudah melakukan konversi antara kedua bentuk tersebut.
Konversi Bentuk Akar ke Bentuk Pangkat dan Sebaliknya
Konversi antara bentuk akar dan bentuk pangkat dilakukan dengan memanfaatkan sifat-sifat eksponen. Secara umum, akar pangkat n dari a ( n√a) dapat ditulis sebagai a 1/n. Sebaliknya, a m/n dapat ditulis sebagai n√a m atau ( n√a) m.
- Contoh konversi dari bentuk akar ke bentuk pangkat: √9 = 9 1/2 = 3
- Contoh konversi dari bentuk pangkat ke bentuk akar: 8 2/3 = ( 3√8) 2 = 2 2 = 4
Contoh Bentuk Akar dan Bentuk Pangkat yang Ekuivalen
Tabel berikut menunjukkan beberapa contoh bentuk akar dan bentuk pangkat yang ekuivalen. Perhatikan bagaimana basis dan eksponen menentukan nilai yang sama dalam kedua representasi.
| Bentuk Akar | Bentuk Pangkat | Basis | Eksponen |
|---|---|---|---|
| √4 | 41/2 | 4 | 1/2 |
| 3√8 | 81/3 | 8 | 1/3 |
| √(x2) | (x2)1/2 | x2 | 1/2 |
| 4√162 | 162/4 = 161/2 | 16 | 1/2 |
Penyederhanaan Bentuk Akar dengan Bentuk Pangkat
Konsep bentuk pangkat sangat membantu dalam menyederhanakan bentuk akar. Dengan mengubah bentuk akar menjadi bentuk pangkat, kita dapat menerapkan sifat-sifat eksponen untuk menyederhanakan ekspresi. Misalnya, untuk menyederhanakan √12, kita dapat mengubahnya menjadi bentuk pangkat terlebih dahulu: √12 = √(4 x 3) = √4 x √3 = 2√
3. Atau dengan menggunakan sifat eksponen: √12 = 12 1/2 = (4 x 3) 1/2 = 4 1/2 x 3 1/2 = 2 x 3 1/2 = 2√3
Contoh Soal Penyederhanaan Bentuk Akar dan Bentuk Pangkat
Sederhanakanlah bentuk akar berikut ini: √75 + √12 – √27. Pertama, kita ubah masing-masing bentuk akar ke dalam bentuk pangkat yang lebih sederhana. √75 = √(25 x 3) = 5√3. √12 = √(4 x 3) = 2√3. √27 = √(9 x 3) = 3√3.
Maka, √75 + √12 – √27 = 5√3 + 2√3 – 3√3 = 4√3.
Pemungkas
Memahami bentuk pangkat membuka cakrawala pemahaman kita terhadap berbagai bidang ilmu. Kemampuan menyederhanakan dan memanipulasi bentuk pangkat merupakan keterampilan penting dalam memecahkan masalah matematika yang kompleks, serta dalam menganalisis dan memprediksi fenomena di dunia nyata. Dengan menguasai konsep ini, kita dapat lebih mudah memahami dan menerapkannya dalam berbagai situasi, baik dalam konteks akademis maupun praktis.