Bentuk sederhana dari akar 75 merupakan konsep dasar dalam matematika yang berkaitan dengan penyederhanaan bentuk akar. Memahami cara menyederhanakan akar 75 sangat penting, karena memudahkan perhitungan dan pemahaman dalam berbagai aplikasi matematika, dari aljabar hingga geometri. Proses penyederhanaan ini melibatkan faktorisasi prima dan pemahaman tentang sifat-sifat akar kuadrat.
Artikel ini akan memandu Anda melalui langkah-langkah penyederhanaan akar 75, mulai dari faktorisasi prima hingga representasi visualnya. Dengan penjelasan yang detail dan contoh-contoh yang relevan, Anda akan memahami konsep ini dengan lebih baik dan mampu menerapkannya dalam berbagai konteks matematika.
Faktorkan 75
Mencari faktorisasi prima dari suatu bilangan merupakan langkah penting dalam memahami sifat-sifat bilangan tersebut. Dalam kasus ini, kita akan memfaktorkan angka 75 menjadi perkalian bilangan prima. Proses ini akan membantu kita memahami pembagian angka 75 dan menemukan semua faktornya.
Faktorisasi Prima dari 75
Faktorisasi prima dari 75 adalah proses penguraian 75 menjadi perkalian bilangan-bilangan prima saja. Bilangan prima adalah bilangan bulat lebih besar dari 1 yang hanya habis dibagi oleh 1 dan dirinya sendiri. Langkah-langkahnya sebagai berikut:
- Mulailah dengan membagi 75 dengan bilangan prima terkecil, yaitu 2. Karena 75 bukan bilangan genap, maka 2 bukan faktornya.
- Selanjutnya, coba bagi 75 dengan bilangan prima berikutnya, yaitu 3. 75 dibagi 3 hasilnya 25. Jadi, 3 adalah faktor prima pertama dari 75.
- Sekarang kita punya 25. 25 bukan bilangan prima karena dapat dibagi 5. 25 dibagi 5 hasilnya 5. Jadi, 5 adalah faktor prima berikutnya.
- Terakhir, 5 adalah bilangan prima. Maka, faktorisasi prima dari 75 adalah 3 x 5 x 5 atau 3 x 52.
Pohon Faktor dari 75
Pohon faktor adalah representasi visual dari proses faktorisasi prima. Kita mulai dari angka 75, kemudian cabang-cabangnya menunjukkan faktor-faktor prima sampai kita mencapai bilangan prima semua.
Bayangkan sebuah pohon dengan akar 75. Cabang pertama bercabang menjadi 3 dan 25. Kemudian, cabang 25 bercabang lagi menjadi 5 dan 5. Jadi, ujung-ujung cabang pohon faktor tersebut menunjukkan faktor prima 3, 5, dan 5.
Semua Faktor dari 75
Setelah mengetahui faktorisasi prima (3 x 5 x 5), kita dapat menemukan semua faktor dari 75 dengan menggabungkan faktor-faktor prima tersebut.
| Faktor |
|---|
| 1 |
| 3 |
| 5 |
| 15 |
| 25 |
| 75 |
Pasangan Faktor dari 75
Pasangan faktor dari 75 adalah dua bilangan yang jika dikalikan menghasilkan
75. Berikut beberapa pasangan faktornya:
- 1 x 75
- 3 x 25
- 5 x 15
Sederhanakan Akar 75: Bentuk Sederhana Dari Akar 75
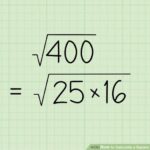
Penyederhanaan bentuk akar merupakan proses mengubah bentuk akar menjadi bentuk yang lebih sederhana dan efisien. Proses ini penting dalam berbagai perhitungan matematika, terutama dalam aljabar dan kalkulus. Pada dasarnya, kita mencari faktor-faktor sempurna dari bilangan di dalam akar untuk menyederhanakannya.
Mari kita sederhanakan bentuk akar √75. Proses ini melibatkan pencarian faktor-faktor sempurna dari 75 yang merupakan kuadrat sempurna. Dengan memahami konsep ini, kita dapat dengan mudah menyederhanakan berbagai bentuk akar lainnya.
Langkah-langkah Penyederhanaan √75
- Cari faktor dari 75. Faktor-faktor 75 adalah 1, 3, 5, 15, 25, dan 75.
- Identifikasi faktor yang merupakan kuadrat sempurna. Dalam hal ini, 25 adalah kuadrat sempurna (5 x 5 = 25).
- Ubah 75 menjadi perkalian dari faktor kuadrat sempurna dan faktor lainnya: 75 = 25 x 3.
- Karena √(a x b) = √a x √b, maka √75 = √(25 x 3) = √25 x √3.
- Sederhanakan √25 menjadi 5. Hasil akhirnya adalah 5√3.
Contoh Penyederhanaan Bentuk Akar Lainnya
Selain √75, mari kita lihat contoh lain. Misalkan kita ingin menyederhanakan √12. Faktor-faktor 12 adalah 1, 2, 3, 4, 6, dan 12. Faktor kuadrat sempurna dari 12 adalah 4 (2 x 2 = 4). Maka, √12 = √(4 x 3) = √4 x √3 = 2√3.
Contoh lain: √18. Faktor-faktor 18 adalah 1, 2, 3, 6, 9, dan 18. Faktor kuadrat sempurna dari 18 adalah 9 (3 x 3 = 9). Maka, √18 = √(9 x 2) = √9 x √2 = 3√2.
Pentingnya Penyederhanaan Bentuk Akar
Penyederhanaan bentuk akar penting karena menghasilkan bentuk yang lebih sederhana dan mudah dipahami. Bentuk sederhana memudahkan perhitungan lebih lanjut, khususnya dalam persamaan dan rumus matematika. Bentuk akar yang sederhana juga memungkinkan perbandingan dan manipulasi aljabar yang lebih efisien.
Bentuk Sederhana Akar 75 dalam Konteks Matematika
Penyederhanaan bentuk akar merupakan konsep penting dalam matematika yang memungkinkan kita untuk menyederhanakan ekspresi matematika yang melibatkan akar. Proses ini membantu dalam menyajikan solusi yang lebih efisien dan mudah dipahami, terutama dalam operasi matematika yang lebih kompleks. Memahami penyederhanaan bentuk akar, seperti √75, sangat krusial untuk menyelesaikan berbagai macam soal matematika.
Penyederhanaan akar 75 didasarkan pada prinsip faktorisasi prima. Dengan mencari faktor prima dari 75, kita dapat menyederhanakan bentuk akar tersebut menjadi bentuk yang lebih sederhana dan efisien untuk digunakan dalam perhitungan selanjutnya. Hal ini akan memudahkan kita dalam melakukan operasi matematika seperti penjumlahan, pengurangan, perkalian, dan pembagian yang melibatkan akar.
Penyederhanaan Akar 75
Untuk menyederhanakan √75, kita perlu mencari faktor prima dari 75. Faktorisasi prima dari 75 adalah 3 x 5 x 5. Dengan demikian, √75 dapat ditulis sebagai √(3 x 5 x 5). Karena 5 x 5 = 25, dan √25 = 5, maka √75 dapat disederhanakan menjadi 5√3.
Aplikasi Penyederhanaan Akar 75 dalam Pemecahan Masalah Matematika
Penyederhanaan bentuk akar, seperti yang telah kita lakukan pada √75, sangat berguna dalam berbagai permasalahan matematika. Bentuk sederhana memudahkan perhitungan dan pemahaman solusi. Berikut contohnya:
Contoh Soal dan Penyelesaian, Bentuk sederhana dari akar 75
Misalkan kita memiliki soal: Hitunglah hasil dari 2√75 + √
12. Untuk menyelesaikan soal ini, kita perlu menyederhanakan √75 terlebih dahulu, seperti yang telah dijelaskan sebelumnya, menjadi 5√
3. Kemudian, kita sederhanakan √12 menjadi 2√
3. Dengan demikian, perhitungan menjadi:
2(5√3) + 2√3 = 10√3 + 2√3 = 12√3
Jadi, hasil dari 2√75 + √12 adalah 12√3.
Penggunaan Bentuk Sederhana Akar 75 dalam Operasi Matematika Lainnya
Bentuk sederhana akar 75 (yaitu 5√3) mempermudah operasi matematika lainnya. Misalnya, jika kita perlu mengalikan √75 dengan √3, perhitungannya akan menjadi lebih mudah:
(5√3) x √3 = 5 x (√3 x √3) = 5 x 3 = 15
Jika kita tidak menyederhanakan √75 terlebih dahulu, perhitungan akan menjadi lebih rumit.
Perbandingan Bentuk Akar 75 Sebelum dan Sesudah Penyederhanaan
| Bentuk Akar | Keterangan |
|---|---|
| √75 | Bentuk akar yang belum disederhanakan |
| 5√3 | Bentuk akar yang sudah disederhanakan |
Representasi Visual Bentuk Sederhana Akar 75
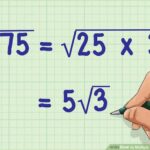
Bentuk sederhana dari akar 75 dapat divisualisasikan melalui beberapa pendekatan geometri dan numerik. Memahami representasi visual ini penting karena membantu kita menghubungkan konsep abstrak akar kuadrat dengan representasi konkret yang lebih mudah dipahami.
Secara umum, kita dapat memvisualisasikan akar 75 melalui representasi luas persegi atau persegi panjang. Akar 75 sendiri merupakan bilangan irasional, artinya tidak dapat dinyatakan sebagai pecahan sederhana. Namun, kita dapat mendekatinya dengan mencari faktor-faktor dari 75 dan menyederhanakannya.
Representasi Geometrik Akar 75
Karena 75 = 25 x 3, maka bentuk sederhana akar 75 adalah 5√3. Secara geometri, kita dapat membayangkan sebuah persegi panjang dengan panjang sisi 5 dan 5√3. Luas persegi panjang ini akan sama dengan 75. Bayangkan pula sebuah persegi dengan luas 75 satuan luas. Panjang sisi persegi ini akan tepat sama dengan √75 atau 5√3.
Kita juga dapat memvisualisasikannya dengan menggunakan segitiga siku-siku. Misalnya, segitiga siku-siku dengan sisi siku-siku sepanjang 5 dan 5√3 akan memiliki hipotenusa dengan panjang 10. Luas segitiga ini akan menjadi ½
– 5
– 5√3 = (25√3)/2. Meskipun tidak langsung mewakili √75, konstruksi geometri ini membantu dalam memahami hubungan antara akar kuadrat dan geometri.
Hubungan Representasi Visual dan Nilai Numerik
Representasi visual, seperti persegi panjang atau segitiga yang dijelaskan di atas, menunjukkan bahwa √75 mewakili panjang sisi suatu bangun datar dengan luas 75. Nilai numerik 5√3 adalah bentuk sederhana dari √75 yang diperoleh melalui faktorisasi prima. Hubungannya adalah bahwa representasi visual memberikan interpretasi geometri dari nilai numerik yang abstrak.
Dengan kata lain, representasi visual membantu kita “melihat” apa yang diwakilkan oleh nilai numerik 5√3. Kita dapat menghubungkan angka abstrak dengan bentuk geometri yang konkret dan mudah dibayangkan.
Ilustrasi Deskriptif Bentuk Sederhana Akar 75
Bayangkan sebuah persegi dengan luas 75 satuan. Kita tidak dapat dengan mudah menentukan panjang sisinya secara tepat karena √75 adalah bilangan irasional. Namun, kita dapat membagi persegi tersebut menjadi 25 persegi kecil dengan sisi sepanjang 1. Kemudian, kita dapat menyusun 3 baris dari persegi-persegi kecil tersebut, menghasilkan persegi panjang dengan sisi 5 dan 15. Selanjutnya, kita dapat memvisualisasikan persegi panjang dengan sisi 5 dan 5√3 yang memiliki luas yang sama dengan persegi awal (75 satuan).
Dengan memvisualisasikannya sebagai persegi panjang dengan sisi 5 dan 5√3, kita dapat melihat bagaimana 5√3 mewakili panjang sisi suatu bangun dengan luas 75. Ini menghubungkan konsep abstrak dari akar kuadrat dengan representasi geometri yang lebih mudah dipahami.
Manfaat Ilustrasi dalam Memahami Konsep
Ilustrasi geometri, seperti yang dijelaskan di atas, membantu dalam memahami konsep bentuk sederhana akar 75 dengan cara yang lebih intuitif daripada hanya melihat angka 5√3. Visualisasi ini menghubungkan konsep aljabar (penyederhanaan akar) dengan konsep geometri (luas dan panjang sisi). Dengan demikian, ilustrasi ini memperkuat pemahaman kita tentang arti dan nilai dari 5√3 sebagai bentuk sederhana dari √75.
Penutup

Penyederhanaan bentuk akar, seperti yang telah diilustrasikan dengan akar 75, merupakan keterampilan penting dalam matematika. Kemampuan untuk menyederhanakan ekspresi akar memungkinkan perhitungan yang lebih efisien dan pemahaman yang lebih mendalam tentang hubungan matematika. Dengan memahami prinsip-prinsip yang mendasari penyederhanaan ini, Anda akan mampu menyelesaikan berbagai masalah matematika dengan lebih mudah dan percaya diri.