- Fungsi Komposisi
-
Menentukan Fungsi Komposisi
- Contoh Soal Fungsi Komposisi dengan Fungsi Linear dan Kuadrat
- Menentukan (f o g)(x) dan (g o f)(x) dengan Fungsi f(x) dan g(x) yang Diketahui
- Contoh Soal Fungsi Komposisi dari Tiga Fungsi atau Lebih
- Langkah-Langkah Penyelesaian Soal Fungsi Komposisi yang Melibatkan Fungsi Trigonometri
- Menentukan Domain dan Range dari Fungsi Komposisi
- Penerapan Fungsi Komposisi dalam Masalah Kontekstual
- Soal Latihan Fungsi Komposisi dan Pembahasan: Contoh Soal Fungsi Komposisi
- Ulasan Penutup
Contoh soal fungsi komposisi merupakan pintu gerbang untuk memahami konsep penting dalam matematika. Fungsi komposisi, yang menggabungkan dua atau lebih fungsi, mungkin tampak rumit pada awalnya, namun dengan latihan dan pemahaman yang tepat, konsep ini akan menjadi mudah dipahami. Materi ini akan membahas pengertian fungsi komposisi, cara menentukannya dalam berbagai situasi, aplikasinya dalam soal cerita, dan tentunya, menyediakan beragam contoh soal beserta pembahasannya untuk mengasah kemampuan.
Dari fungsi linear sederhana hingga fungsi trigonometri yang lebih kompleks, kita akan menjelajahi berbagai tipe soal fungsi komposisi. Kita akan mempelajari bagaimana menentukan (f o g)(x) dan (g o f)(x), menentukan domain dan range, serta mengaplikasikan konsep ini dalam pemecahan masalah kontekstual, seperti pertumbuhan populasi atau transformasi geometri. Dengan contoh-contoh yang terstruktur dan penjelasan yang detail, diharapkan pembaca dapat menguasai konsep fungsi komposisi dengan baik.
Fungsi Komposisi
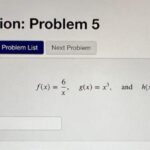
Fungsi komposisi merupakan operasi matematika yang menggabungkan dua atau lebih fungsi untuk menghasilkan fungsi baru. Operasi ini menghasilkan fungsi yang hasilnya didapatkan dengan memasukkan keluaran dari satu fungsi sebagai masukan ke fungsi lainnya. Konsep ini penting dalam memahami bagaimana fungsi-fungsi dapat berinteraksi dan membentuk fungsi yang lebih kompleks.
Definisi dan Contoh Sederhana Fungsi Komposisi
Fungsi komposisi didefinisikan sebagai penggabungan dua fungsi, katakanlah fungsi f dan g, untuk menghasilkan fungsi baru, yang seringkali dinotasikan sebagai ( f o g)( x) atau f( g( x)). Ini berarti kita pertama-tama menghitung g( x), kemudian hasil tersebut digunakan sebagai input untuk fungsi f. Sebagai contoh sederhana, jika f( x) = x + 2 dan g( x) = 2 x, maka ( f o g)( x) = f( g( x)) = f(2 x) = 2 x + 2.
Ilustrasi Fungsi Komposisi dengan Diagram Panah
Bayangkan dua fungsi, f dan g, diilustrasikan dengan diagram panah. Fungsi g memetakan elemen dari himpunan A ke himpunan B, sedangkan fungsi f memetakan elemen dari himpunan B ke himpunan C. Fungsi komposisi ( f o g) akan memetakan elemen dari himpunan A langsung ke himpunan C, dengan terlebih dahulu melalui proses pemetaan oleh fungsi g, kemudian dilanjutkan oleh fungsi f.
Proses ini menggambarkan bagaimana keluaran dari g menjadi masukan untuk f, menghasilkan pemetaan langsung dari A ke C.
Perbandingan Fungsi Komposisi dengan Operasi Fungsi Lainnya, Contoh soal fungsi komposisi
| Operasi | Definisi | Contoh (dengan f(x) = x + 1 dan g(x) = x – 1) | Sifat |
|---|---|---|---|
| Penjumlahan | (f + g)(x) = f(x) + g(x) | (f + g)(x) = (x + 1) + (x – 1) = 2x | Komutatif |
| Pengurangan | (f – g)(x) = f(x)
|
(f – g)(x) = (x + 1)
|
Non-komutatif |
| Perkalian | (f
|
(f
|
Komutatif |
| Pembagian | (f / g)(x) = f(x) / g(x) | (f / g)(x) = (x + 1) / (x – 1) | Non-komutatif |
| Komposisi | (f o g)(x) = f(g(x)) | (f o g)(x) = f(x – 1) = (x – 1) + 1 = x | Non-komutatif, Asosiatif |
Sifat-Sifat Dasar Fungsi Komposisi
Fungsi komposisi memiliki beberapa sifat dasar yang perlu dipahami. Salah satu sifat yang penting adalah sifat asosiatif, yang menyatakan bahwa (f o g) o h = f o (g o h). Ini berarti urutan pengelompokan fungsi tidak mempengaruhi hasil akhir selama urutan fungsi tetap sama. Namun, fungsi komposisi bersifat non-komutatif, yang berarti bahwa (f o g)(x) ≠ (g o f)(x) secara umum.
Urutan fungsi sangat penting dan mengubah urutannya akan menghasilkan fungsi yang berbeda.
Contoh Soal Fungsi Komposisi dengan Dua Fungsi Linear
Misalkan kita memiliki dua fungsi linear: f(x) = 3x + 1 dan g(x) = x –
2. Tentukan (f o g)(x) dan (g o f)(x). Untuk (f o g)(x), kita substitusikan g(x) ke dalam f(x): (f o g)(x) = f(g(x)) = f(x – 2) = 3(x – 2) + 1 = 3x –
5. Sedangkan untuk (g o f)(x), kita substitusikan f(x) ke dalam g(x): (g o f)(x) = g(f(x)) = g(3x + 1) = (3x + 1)
-2 = 3x – 1.
Perhatikan bahwa (f o g)(x) ≠ (g o f)(x), yang menunjukkan sifat non-komutatif dari fungsi komposisi.
Menentukan Fungsi Komposisi
Fungsi komposisi merupakan operasi matematika yang menggabungkan dua atau lebih fungsi untuk menghasilkan fungsi baru. Pemahaman tentang fungsi komposisi penting dalam berbagai bidang, termasuk kalkulus, fisika, dan ilmu komputer. Artikel ini akan membahas cara menentukan fungsi komposisi, termasuk contoh soal yang melibatkan berbagai jenis fungsi dan langkah-langkah penyelesaiannya secara detail.
Contoh Soal Fungsi Komposisi dengan Fungsi Linear dan Kuadrat
Misalkan kita memiliki fungsi linear f(x) = 2x + 1 dan fungsi kuadrat g(x) = x²
-3. Kita akan menentukan (f o g)(x) dan (g o f)(x).
(f o g)(x) berarti kita substitusikan g(x) ke dalam f(x). Jadi:
(f o g)(x) = f(g(x)) = f(x²
- 3) = 2(x²
- 3) + 1 = 2x²
- 6 + 1 = 2x²
- 5
Sedangkan (g o f)(x) berarti kita substitusikan f(x) ke dalam g(x). Jadi:
(g o f)(x) = g(f(x)) = g(2x + 1) = (2x + 1)²
3 = 4x² + 4x + 1 – 3 = 4x² + 4x – 2
Dari contoh ini, terlihat bahwa (f o g)(x) ≠ (g o f)(x), menunjukkan bahwa operasi komposisi fungsi tidak bersifat komutatif.
Menentukan (f o g)(x) dan (g o f)(x) dengan Fungsi f(x) dan g(x) yang Diketahui
Untuk menentukan (f o g)(x) dan (g o f)(x), langkah-langkah umum yang harus diikuti adalah sebagai berikut:
- Tentukan rumus fungsi f(x) dan g(x).
- Untuk (f o g)(x), substitusikan g(x) ke dalam rumus f(x) dan sederhanakan hasilnya.
- Untuk (g o f)(x), substitusikan f(x) ke dalam rumus g(x) dan sederhanakan hasilnya.
Proses ini berlaku untuk berbagai jenis fungsi, termasuk fungsi linear, kuadrat, kubik, dan lainnya. Penting untuk memperhatikan urutan substitusi agar hasil yang diperoleh akurat.
Contoh Soal Fungsi Komposisi dari Tiga Fungsi atau Lebih
Misalkan kita memiliki tiga fungsi: f(x) = x + 2, g(x) = x², dan h(x) = 3x. Kita ingin menentukan (f o g o h)(x).
Langkah penyelesaiannya adalah dengan melakukan komposisi secara bertahap:
(f o g o h)(x) = f(g(h(x))) = f(g(3x)) = f((3x)²) = f(9x²) = 9x² + 2
Komposisi fungsi lebih dari dua fungsi dilakukan dengan cara yang sama, yaitu dengan melakukan substitusi secara bertahap, dimulai dari fungsi paling dalam.
Langkah-Langkah Penyelesaian Soal Fungsi Komposisi yang Melibatkan Fungsi Trigonometri
Fungsi komposisi juga dapat melibatkan fungsi trigonometri. Misalnya, jika f(x) = sin(x) dan g(x) = x², maka (f o g)(x) = sin(x²) dan (g o f)(x) = (sin(x))² = sin²(x).
Langkah penyelesaiannya sama seperti pada fungsi aljabar lainnya, yaitu dengan mensubstitusikan fungsi ke dalam fungsi lainnya. Perlu diingat untuk memperhatikan identitas trigonometri yang mungkin dapat digunakan untuk menyederhanakan hasil.
Menentukan Domain dan Range dari Fungsi Komposisi
Domain dari fungsi komposisi (f o g)(x) adalah himpunan semua nilai x yang berada di domain g(x) dan yang menghasilkan nilai g(x) yang berada di domain f(x). Range dari fungsi komposisi adalah himpunan semua nilai yang dihasilkan oleh (f o g)(x).
Untuk menentukan domain dan range, perlu dilakukan analisis terhadap domain dan range dari masing-masing fungsi penyusunnya. Terkadang, domain fungsi komposisi lebih kecil daripada domain fungsi asalnya karena adanya batasan yang disebabkan oleh komposisi.
Penerapan Fungsi Komposisi dalam Masalah Kontekstual
Fungsi komposisi, yang menggabungkan dua atau lebih fungsi untuk menghasilkan fungsi baru, memiliki penerapan luas dalam berbagai konteks kehidupan nyata. Memahami konsep ini memungkinkan kita untuk memodelkan dan menyelesaikan masalah yang kompleks dengan cara yang lebih efisien dan terstruktur. Berikut beberapa contoh penerapan fungsi komposisi dalam masalah kontekstual.
Contoh Soal Cerita yang Menggunakan Fungsi Komposisi
Sebuah toko pakaian memberikan diskon 20% untuk semua barang, kemudian memberikan diskon tambahan 10% untuk barang yang sudah didiskon. Jika harga awal sebuah kemeja adalah Rp 200.000, tentukan harga akhir kemeja tersebut setelah kedua diskon diterapkan. Soal ini dapat dimodelkan menggunakan fungsi komposisi.
Langkah penyelesaiannya melibatkan definisi dua fungsi: fungsi diskon pertama (f(x) = 0.8x) dan fungsi diskon kedua (g(x) = 0.9x). Harga akhir kemeja didapatkan dengan mengkomposisikan kedua fungsi, yaitu (g o f)(x) = g(f(x)) = 0.9(0.8x) = 0.72x. Dengan x = Rp 200.000, harga akhir kemeja adalah 0.72
– Rp 200.000 = Rp 144.000.
Contoh Soal Transformasi Geometri Menggunakan Fungsi Komposisi
Bayangkan sebuah titik A(2,3) diputar 90 derajat berlawanan arah jarum jam terhadap titik asal (0,0), kemudian ditranslasikan sejauh 2 satuan ke kanan dan 1 satuan ke bawah. Transformasi ini dapat direpresentasikan sebagai fungsi komposisi dari rotasi dan translasi.
Rotasi 90 derajat berlawanan arah jarum jam dapat direpresentasikan sebagai fungsi R(x,y) = (-y, x). Translasi 2 satuan ke kanan dan 1 satuan ke bawah dapat direpresentasikan sebagai fungsi T(x,y) = (x+2, y-1). Dengan mengkomposisikan kedua fungsi, (T o R)(x,y) = T(R(x,y)) = T(-y, x) = (-y+2, x-1). Dengan menerapkan fungsi komposisi ini pada titik A(2,3), kita mendapatkan titik baru A’(-3+2, 2-1) = A’(-1,1).
Contoh Soal Pertumbuhan Populasi atau Peluruhan Radioaktif Menggunakan Fungsi Komposisi
Misalkan populasi bakteri tertentu meningkat dua kali lipat setiap jam. Jika populasi awal adalah 1000 bakteri, dan kita ingin mengetahui populasi setelah 3 jam, kita dapat menggunakan fungsi komposisi. Fungsi pertumbuhan populasi dapat dinyatakan sebagai f(x) = 2x, dimana x adalah populasi awal. Untuk mengetahui populasi setelah 3 jam, kita dapat mengkomposisikan fungsi tersebut tiga kali: (f o f o f)(1000) = f(f(f(1000))) = 2(2(2(1000))) = 8000 bakteri.
Pada kasus peluruhan radioaktif, pendekatan serupa dapat digunakan, hanya saja fungsi yang digunakan akan merepresentasikan penurunan jumlah zat radioaktif seiring waktu. Misalnya, jika zat radioaktif meluruh setengahnya setiap hari, fungsi peluruhannya adalah f(x) = 0.5x, dan komposisi fungsi dapat digunakan untuk memprediksi jumlah zat yang tersisa setelah beberapa hari.
Perbedaan Pendekatan Penyelesaian Soal Cerita Menggunakan Fungsi Komposisi dan Metode Lainnya
Metode lain yang mungkin digunakan untuk menyelesaikan soal-soal di atas antara lain adalah dengan menghitung secara bertahap atau menggunakan persamaan yang lebih kompleks. Namun, penggunaan fungsi komposisi menawarkan pendekatan yang lebih terstruktur, elegan, dan mudah dipahami, terutama untuk masalah yang melibatkan beberapa tahapan transformasi atau perubahan. Fungsi komposisi memungkinkan kita untuk memecah masalah kompleks menjadi bagian-bagian yang lebih kecil dan mudah dikelola, lalu menggabungkannya untuk mendapatkan solusi akhir.
Soal Latihan Fungsi Komposisi dan Pembahasan: Contoh Soal Fungsi Komposisi

Berikut ini disajikan lima soal latihan fungsi komposisi dengan berbagai tingkat kesulitan, lengkap dengan pembahasannya. Soal-soal disusun dalam bentuk pilihan ganda dan uraian untuk menguji pemahaman Anda secara komprehensif. Pembahasan meliputi langkah-langkah penyelesaian yang detail dan penjelasan konseptual yang relevan.
Soal Latihan Fungsi Komposisi
Soal-soal latihan ini dirancang untuk menguji kemampuan Anda dalam memahami dan menerapkan konsep fungsi komposisi. Tingkat kesulitan bervariasi, mulai dari yang sederhana hingga yang lebih kompleks, sehingga Anda dapat mengukur pemahaman Anda secara bertahap.
- Diketahui fungsi f(x) = 2x + 1 dan g(x) = x²3. Tentukan nilai (f o g)(2).
- Jika h(x) = 3x – 2 dan (h o f)(x) = 6x + 1, tentukan fungsi f(x).
- Fungsi f dan g didefinisikan sebagai f(x) = √(x+1) dan g(x) = x²4. Tentukan daerah asal (domain) dari (f o g)(x).
- (Soal Uraian) Tentukan fungsi invers dari (f o g)(x) jika f(x) = x + 2 dan g(x) = 2x – 1.
- (Soal Pilihan Ganda) Jika f(x) = x – 1 dan g(x) = 2x, maka (g o f)(x) = …
- 2x – 1
- 2x – 2
- x – 1
- 2x + 1
Pembahasan Soal Latihan Fungsi Komposisi
Berikut ini adalah pembahasan lengkap untuk masing-masing soal latihan di atas. Pembahasan disusun secara bertahap dan detail agar mudah dipahami.
- (f o g)(2) = f(g(2)) = f(2² – 3) = f(1) = 2(1) + 1 = 3
- (h o f)(x) = h(f(x)) = 3f(x)2 = 6x + 1. Maka 3f(x) = 6x + 3, sehingga f(x) = 2x + 1.
- (f o g)(x) = f(g(x)) = √(x²
- 4 + 1) = √(x²
- 3). Agar akar kuadrat terdefinisi, x²
- 3 ≥ 0, sehingga x ≤ -√3 atau x ≥ √3. Jadi, daerah asal (f o g)(x) adalah (-∞, -√3] ∪ [√3, ∞).
- (f o g)(x) = f(g(x)) = (2x – 1) + 2 = 2x + 1. Untuk mencari invers, misalkan y = 2x + 1. Maka x = (y – 1)/2. Jadi, invers dari (f o g)(x) adalah ((x – 1)/2).
- (g o f)(x) = g(f(x)) = g(x – 1) = 2(x – 1) = 2x – 2. Jawaban yang tepat adalah B.
Tips dan Trik Menyelesaikan Soal Fungsi Komposisi
Gunakan definisi fungsi komposisi (f o g)(x) = f(g(x)) secara konsisten. Perhatikan urutan operasi dan pastikan untuk mensubstitusikan nilai atau fungsi yang tepat. Latih berbagai jenis soal untuk meningkatkan pemahaman dan kemampuan Anda. Jangan lupa untuk memeriksa kembali hasil Anda.
Rumus-Rumus Penting Fungsi Komposisi
(f o g)(x) = f(g(x))
(g o f)(x) = g(f(x))
Jika f dan g memiliki invers, maka (f o g)⁻¹(x) = g⁻¹(f⁻¹(x))
Ulasan Penutup

Setelah mempelajari berbagai contoh soal fungsi komposisi dan pembahasannya, diharapkan pemahaman Anda tentang konsep ini semakin matang. Kemampuan untuk menggabungkan dan menganalisis fungsi-fungsi akan sangat berguna tidak hanya dalam matematika lanjutan, tetapi juga dalam berbagai bidang ilmu lainnya yang membutuhkan pemodelan matematis. Dengan latihan yang konsisten dan pemahaman yang mendalam terhadap sifat-sifat fungsi komposisi, Anda akan mampu menyelesaikan soal-soal yang lebih kompleks dengan percaya diri.