Contoh Soal Mean Median Modus Pembahasan Lengkap

Contoh Soal Mean Median Modus: Mempelajari mean, median, dan modus merupakan langkah penting dalam memahami statistika. Ketiga ukuran pemusatan data ini menawarkan cara berbeda untuk menggambarkan karakteristik sekumpulan angka, masing-masing memiliki kegunaan dan interpretasi tersendiri. Artikel ini akan membahas pengertian, perhitungan, dan penerapan ketiga ukuran ini dalam berbagai konteks, dilengkapi dengan contoh soal dan pembahasan yang komprehensif.

Kita akan menjelajahi perbedaan mendasar antara mean (rata-rata), median (nilai tengah), dan modus (nilai yang paling sering muncul). Kemudian, kita akan mempelajari langkah-langkah perhitungannya, baik untuk data tunggal maupun data kelompok. Lebih lanjut, akan dibahas penerapannya dalam kehidupan sehari-hari dan contoh soal yang lebih kompleks untuk mengasah pemahaman Anda.

Pengertian Mean, Median, dan Modus

Mean, median, dan modus merupakan tiga ukuran pemusatan data yang umum digunakan dalam statistika deskriptif. Ketiganya memberikan gambaran tentang nilai tengah atau nilai yang paling sering muncul dalam suatu kumpulan data, namun dengan cara yang berbeda dan memiliki kegunaan masing-masing.

Perbedaan Mean, Median, dan Modus

Ketiga ukuran ini mencerminkan pusat data dari sudut pandang yang berbeda. Mean merupakan rata-rata aritmatika, menghitung total nilai data kemudian dibagi jumlah data. Median adalah nilai tengah data setelah diurutkan, sedangkan modus adalah nilai yang paling sering muncul.

Contoh Perhitungan Mean, Median, dan Modus

Mari kita gunakan contoh data numerik berikut: 2, 4, 4, 5, 6, 7, 8. Dengan data ini, kita akan menghitung mean, median, dan modus.

Tabel Perhitungan Mean, Median, dan Modus

Kegunaan Mean, Median, dan Modus dalam Analisis Data

Pemilihan ukuran pemusatan data yang tepat bergantung pada jenis data dan tujuan analisis. Mean sensitif terhadap nilai ekstrem (outlier), sehingga kurang tepat digunakan pada data yang mengandung outlier signifikan. Median lebih robust terhadap outlier, memberikan gambaran yang lebih representatif pada data yang terdistribusi tidak simetris. Modus berguna untuk menunjukkan nilai yang paling populer atau umum dalam suatu data kategorikal atau numerik.

Situasi Penggunaan Mean, Median, dan Modus

• Mean: Ideal untuk data numerik yang terdistribusi normal dan tidak memiliki outlier yang signifikan. Contoh: menghitung rata-rata nilai ujian siswa dalam suatu kelas.
• Median: Lebih tepat digunakan pada data yang terdistribusi tidak simetris atau mengandung outlier. Contoh: menganalisis harga rumah di suatu wilayah, dimana beberapa rumah mungkin memiliki harga yang jauh lebih tinggi daripada rata-rata.
• Modus: Cocok untuk data kategorikal atau numerik dengan beberapa nilai yang berulang. Contoh: menentukan ukuran sepatu yang paling banyak terjual di sebuah toko.

Cara Menghitung Mean, Median, dan Modus

Mean, median, dan modus merupakan tiga ukuran pemusatan data yang sering digunakan dalam statistika deskriptif. Ketiganya memberikan gambaran berbeda mengenai pusat data, sehingga pemahaman tentang cara menghitung dan interpretasinya sangat penting dalam menganalisis data. Pemilihan ukuran pemusatan data yang tepat bergantung pada jenis data dan tujuan analisis.

Perhitungan Mean

Mean atau rata-rata hitung merupakan ukuran pemusatan data yang diperoleh dengan menjumlahkan semua nilai data kemudian dibagi dengan banyaknya data. Perhitungan mean berbeda untuk data tunggal dan data kelompok.

• Data Tunggal: Jumlah semua nilai data dibagi dengan banyaknya data.
• Data Kelompok: Menghitung mean data kelompok memerlukan perhitungan yang sedikit lebih kompleks. Kita perlu menggunakan nilai tengah setiap interval kelas, dikalikan dengan frekuensi kelas tersebut, kemudian dijumlahkan dan dibagi dengan jumlah total frekuensi.

Contoh Soal Mean Data Tunggal:
Nilai ulangan matematika 5 siswa adalah: 7, 8, 9, 6, 10.
Hitunglah mean nilai ulangan tersebut!
Penyelesaian:
Mean = (7 + 8 + 9 + 6 + 10) / 5 = 8

Contoh Soal Mean Data Kelompok:
Berikut data berat badan (kg) 20 siswa:

Interval Berat Badan (kg)	Frekuensi
40-44	2
45-49	5
50-54	8
55-59	5

Hitunglah mean berat badan siswa tersebut!
Penyelesaian:
Pertama, tentukan nilai tengah setiap interval. Kemudian kalikan dengan frekuensi masing-masing interval, lalu jumlahkan dan bagi dengan total frekuensi.
Nilai tengah interval 40-44 = 42
Nilai tengah interval 45-49 = 47
Nilai tengah interval 50-54 = 52
Nilai tengah interval 55-59 = 57
Mean = [(42*2) + (47*5) + (52*8) + (57*5)] / 20 = 50.35 kg

Perhitungan Median

Median merupakan nilai tengah dari data setelah diurutkan dari nilai terkecil hingga terbesar. Perhitungan median juga berbeda untuk data tunggal dan data kelompok.

• Data Tunggal: Setelah data diurutkan, median adalah nilai tengah. Jika jumlah data ganjil, median adalah nilai tengah. Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah.
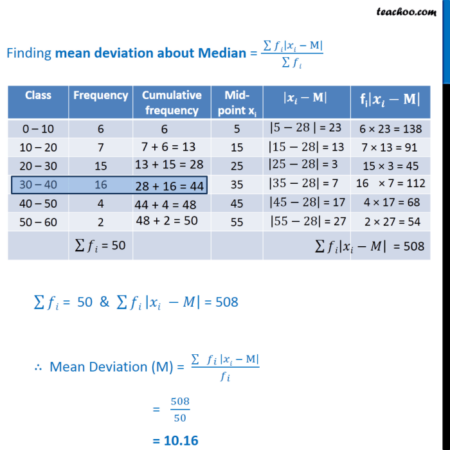
• Data Kelompok: Perhitungan median data kelompok melibatkan interpolasi. Kita perlu menentukan kelas median (kelas yang memuat nilai tengah data), kemudian menggunakan rumus interpolasi untuk menghitung nilai median.

Contoh Soal Median Data Tunggal:
Nilai ulangan matematika 5 siswa adalah: 7, 8, 9, 6, 10.
Hitunglah median nilai ulangan tersebut!
Penyelesaian:
Urutkan data: 6, 7, 8, 9, 10
Median = 8

Contoh Soal Median Data Kelompok:
(Menggunakan data berat badan dari contoh soal mean data kelompok)
Hitunglah median berat badan siswa tersebut!
Penyelesaian:
Total frekuensi = 20. Median terletak pada data ke-10. Kelas median adalah kelas yang memuat data ke-10, yaitu kelas 50-54.
Rumus interpolasi: Median = L + [(n/2 – Fk) / f]

i

dimana:
L = batas bawah kelas median = 49.5
n = jumlah data = 20
Fk = frekuensi kumulatif sebelum kelas median = 7
f = frekuensi kelas median = 8
i = panjang interval = 5
Median = 49.5 + [(10 – 7) / 8] – 5 = 51.375 kg

Perhitungan Modus, Contoh soal mean median modus

Modus adalah nilai yang paling sering muncul dalam suatu data. Perhitungan modus relatif sederhana, baik untuk data tunggal maupun data kelompok.

• Data Tunggal: Modus adalah nilai yang paling sering muncul. Suatu data bisa memiliki lebih dari satu modus (multimodal) atau tidak memiliki modus (a-modal).
• Data Kelompok: Modus data kelompok adalah nilai tengah dari interval kelas yang memiliki frekuensi terbesar.

Contoh Soal Modus Data Tunggal:
Nilai ulangan matematika 5 siswa adalah: 7, 8, 9, 6, 10.
Hitunglah modus nilai ulangan tersebut!
Penyelesaian:
Tidak ada modus karena semua nilai muncul hanya sekali.

Contoh Soal Modus Data Kelompok:
(Menggunakan data berat badan dari contoh soal mean data kelompok)
Hitunglah modus berat badan siswa tersebut!
Penyelesaian:
Modus berada pada interval kelas dengan frekuensi terbesar, yaitu interval 50-54. Modus = 52 kg (nilai tengah interval)

Perbedaan Perhitungan pada Data dengan Nilai Ekstrem

Nilai ekstrem (nilai yang sangat tinggi atau rendah dibandingkan dengan nilai lainnya) dapat sangat memengaruhi perhitungan mean. Median dan modus kurang sensitif terhadap nilai ekstrem. Sebagai contoh, jika dalam data nilai ulangan terdapat nilai ekstrem yang sangat tinggi, mean akan meningkat secara signifikan, sedangkan median dan modus mungkin tidak berubah banyak.

Penerapan Mean, Median, dan Modus dalam Kehidupan Sehari-hari

Mean, median, dan modus merupakan tiga ukuran pemusatan data yang sering kita temui dalam kehidupan sehari-hari, meskipun mungkin tanpa kita sadari. Ketiga ukuran ini memberikan gambaran yang berbeda tentang kecenderungan data, sehingga pemahamannya penting untuk pengambilan keputusan yang lebih baik. Penerapannya sangat luas, mulai dari hal sederhana seperti menghitung nilai rata-rata ujian hingga menganalisis tren penjualan di sebuah perusahaan.

Contoh Penerapan Mean dalam Kehidupan Sehari-hari

Mean, atau rata-rata, merupakan ukuran pemusatan data yang paling umum digunakan. Ia dihitung dengan menjumlahkan semua nilai data kemudian dibagi dengan jumlah data tersebut. Berikut beberapa contoh penerapannya:

• Menghitung nilai rata-rata ujian: Misalnya, jika seorang siswa mendapatkan nilai 70, 80, 90, dan 100 pada empat ujian, nilai rata-ratanya adalah (70+80+90+100)/4 = 85.
• Menghitung rata-rata pengeluaran bulanan: Dengan menjumlahkan seluruh pengeluaran selama sebulan dan membaginya dengan jumlah hari dalam bulan tersebut, kita dapat mengetahui rata-rata pengeluaran harian.
• Menghitung kecepatan rata-rata perjalanan: Total jarak tempuh dibagi dengan total waktu perjalanan akan menghasilkan kecepatan rata-rata.

Contoh Penerapan Median dalam Kehidupan Sehari-hari

Median merupakan nilai tengah dari sekumpulan data yang telah diurutkan dari yang terkecil hingga yang terbesar. Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah. Berikut beberapa contoh penerapannya:

• Menentukan harga rumah di suatu wilayah: Dengan mengurutkan harga rumah dari yang termurah hingga termahal, harga median memberikan gambaran yang lebih akurat tentang harga rumah “tipikal” di wilayah tersebut dibandingkan dengan mean, karena median tidak dipengaruhi oleh harga rumah yang sangat tinggi atau sangat rendah (outlier).
• Menganalisis pendapatan rumah tangga: Median pendapatan memberikan gambaran yang lebih representatif tentang pendapatan rumah tangga dibandingkan dengan mean, karena median tidak terpengaruh oleh pendapatan ekstrem yang sangat tinggi atau sangat rendah.
• Menentukan ukuran pakaian yang paling banyak terjual di toko: Dengan mengurutkan ukuran pakaian yang terjual, median akan menunjukkan ukuran yang berada di tengah-tengah distribusi penjualan.

Contoh Penerapan Modus dalam Kehidupan Sehari-hari

Modus adalah nilai yang paling sering muncul dalam suatu set data. Suatu set data dapat memiliki lebih dari satu modus atau tidak memiliki modus sama sekali. Berikut beberapa contoh penerapannya:

• Menentukan ukuran sepatu yang paling laris di toko sepatu: Ukuran sepatu yang paling banyak terjual merupakan modus dari data penjualan sepatu.
• Menentukan warna mobil yang paling banyak dipesan: Warna mobil yang paling banyak dipesan menunjukkan modus dari data pemesanan mobil.
• Menetapkan menu makanan paling populer di restoran: Menu makanan yang paling sering dipesan oleh pelanggan menunjukkan modus dari data pesanan makanan.

Contoh Kasus dan Perhitungan Mean, Median, dan Modus

Sebuah toko buku mencatat jumlah buku yang terjual setiap hari selama seminggu sebagai berikut: 15, 20, 25, 18, 22, 25, 20.

Untuk menganalisis data penjualan, kita perlu menghitung mean, median, dan modus.

1. Mean: (15 + 20 + 25 + 18 + 22 + 25 + 20) / 7 = 20.71 buku (dibulatkan ke satu desimal)
2. Median: Urutkan data: 15, 18, 20, 20, 22, 25, 25. Median adalah nilai tengah, yaitu 20 buku.
3. Modus: Nilai yang paling sering muncul adalah 20 dan 25. Data ini memiliki dua modus.

Dari perhitungan di atas, kita dapat melihat bahwa rata-rata penjualan buku per hari adalah sekitar 20.71 buku. Namun, median menunjukkan bahwa setengah dari hari penjualan berada di bawah 20 buku dan setengahnya di atas 20 buku. Terakhir, modus menunjukkan bahwa penjualan buku yang paling sering terjadi adalah 20 dan 25 buku.

Contoh Soal dan Pembahasan yang Lebih Kompleks: Contoh Soal Mean Median Modus

Setelah memahami perhitungan mean, median, dan modus secara terpisah, mari kita terapkan pemahaman tersebut pada soal cerita yang lebih kompleks. Soal-soal berikut ini dirancang untuk menguji kemampuan Anda dalam menganalisis data dan memilih ukuran pemusatan data yang paling tepat berdasarkan konteks permasalahan.

Analisis Penjualan Produk Baru

Sebuah perusahaan baru saja meluncurkan produk baru. Data penjualan harian selama 10 hari pertama adalah sebagai berikut: 25, 30, 32, 35, 35, 40, 40, 40, 50, 100. Analisislah data penjualan ini dengan menghitung mean, median, dan modus. Tentukan ukuran pemusatan data mana yang paling representatif untuk menggambarkan penjualan produk tersebut dan jelaskan alasannya.

1. Perhitungan Mean: Jumlah total penjualan adalah 427. Mean = 427/10 = 42.7
2. Perhitungan Median: Urutkan data terlebih dahulu: 25, 30, 32, 35, 35, 40, 40, 40, 50, 100. Median adalah rata-rata dari dua nilai tengah (35 dan 40), yaitu (35+40)/2 = 37.5
3. Perhitungan Modus: Modus adalah nilai yang paling sering muncul, yaitu 40.
4. Analisis: Data penjualan menunjukkan adanya outlier, yaitu nilai 100 yang jauh lebih tinggi daripada nilai lainnya. Hal ini menyebabkan mean menjadi lebih tinggi daripada median dan modus. Dalam kasus ini, median (37.5) atau modus (40) lebih representatif untuk menggambarkan penjualan produk karena mean dipengaruhi oleh outlier. Median dan modus memberikan gambaran yang lebih akurat tentang penjualan harian yang sebenarnya.

Distribusi Data Miring dan Pengaruhnya

Data penjualan di atas menunjukkan distribusi data yang miring ke kanan (positively skewed) karena adanya outlier. Distribusi data miring terjadi ketika sebagian besar data terkonsentrasi di salah satu sisi, sementara di sisi lainnya terdapat nilai-nilai ekstrem. Berikut ilustrasi bagaimana distribusi data miring memengaruhi mean, median, dan modus:

Pada distribusi data miring ke kanan, mean akan lebih besar daripada median, dan median akan lebih besar daripada modus. Sebaliknya, pada distribusi data miring ke kiri, mean akan lebih kecil daripada median, dan median akan lebih kecil daripada modus. Dalam kasus distribusi data yang simetris, mean, median, dan modus akan memiliki nilai yang sama.

Perbedaan nilai mean, median, dan modus dalam contoh penjualan produk baru memberikan informasi penting tentang karakteristik data. Kehadiran outlier menyebabkan mean tidak lagi menjadi representasi yang akurat dari pusat data, sehingga median atau modus menjadi pilihan yang lebih baik.

Ringkasan Terakhir

Memahami konsep mean, median, dan modus merupakan kunci untuk menganalisis data secara efektif. Dengan memahami perbedaan dan penerapan masing-masing ukuran pemusatan data, kita dapat mengungkap informasi berharga dari sekumpulan angka. Melalui contoh soal dan pembahasan yang telah diuraikan, diharapkan pemahaman Anda tentang mean, median, dan modus semakin meningkat dan dapat diterapkan dalam berbagai situasi, baik dalam konteks akademis maupun kehidupan sehari-hari.