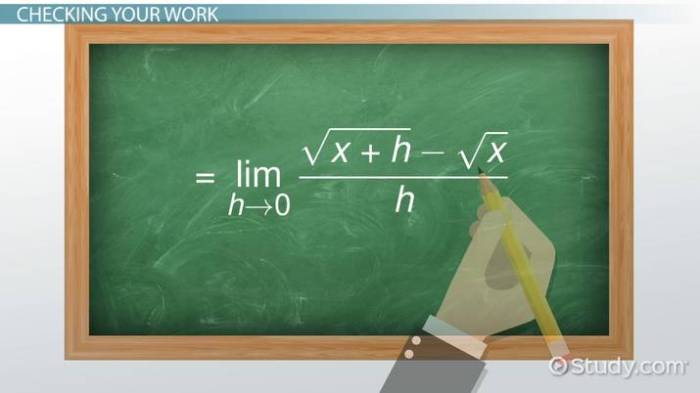
Contoh soal turunan fungsi aljabar merupakan kunci pemahaman kalkulus. Materi ini mengajak kita menjelajahi dunia turunan, mulai dari definisi dasar hingga aplikasi praktisnya dalam memecahkan berbagai permasalahan. Kita akan mempelajari rumus-rumus penting, aturan-aturan turunan, dan bagaimana menerapkannya pada fungsi aljabar, baik yang sederhana maupun kompleks. Dengan latihan soal yang beragam, pemahaman konsep turunan akan semakin terasah.
Dari pengertian turunan fungsi aljabar, rumus dan aturannya, hingga penerapannya dalam menyelesaikan masalah nyata, bahasan ini dirancang untuk memberikan gambaran lengkap dan komprehensif. Contoh soal yang disajikan akan membantu Anda memahami konsep turunan dan mengasah kemampuan dalam menyelesaikan soal-soal yang lebih menantang.
Pengertian Turunan Fungsi Aljabar
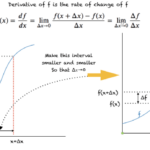
Turunan fungsi aljabar merupakan konsep fundamental dalam kalkulus yang menjelaskan laju perubahan suatu fungsi terhadap perubahan variabel bebasnya. Konsep ini memiliki aplikasi luas dalam berbagai bidang, mulai dari fisika dan teknik hingga ekonomi dan ilmu komputer. Pemahaman yang baik tentang turunan sangat penting untuk menyelesaikan berbagai masalah yang melibatkan laju perubahan, optimasi, dan aproksimasi.
Secara sederhana, turunan fungsi di suatu titik merepresentasikan gradien garis singgung kurva fungsi pada titik tersebut. Nilai turunan ini mengindikasikan seberapa cepat nilai fungsi berubah di sekitar titik tersebut. Nilai turunan yang positif menunjukkan fungsi meningkat, nilai negatif menunjukkan fungsi menurun, dan nilai nol menunjukkan titik stasioner (maksimum, minimum, atau titik belok).
Contoh Fungsi Aljabar
Fungsi aljabar dapat berupa fungsi sederhana maupun rumit. Fungsi sederhana biasanya melibatkan pangkat bulat positif dari variabel bebas, sedangkan fungsi rumit dapat melibatkan kombinasi berbagai operasi aljabar, seperti penjumlahan, pengurangan, perkalian, pembagian, dan perpangkatan.
- Contoh Fungsi Sederhana: f(x) = 2x + 3 (fungsi linear)
- Contoh Fungsi Rumit: f(x) = x³
-4x² + 7x – 2
Perbedaan Fungsi Aljabar Linear dan Non-Linear
Perbedaan utama antara fungsi aljabar linear dan non-linear terletak pada bentuk grafiknya dan bagaimana perubahan pada variabel bebas memengaruhi variabel terikat. Fungsi linear selalu menghasilkan garis lurus ketika digambarkan dalam sistem koordinat kartesius, sementara fungsi non-linear menghasilkan kurva.
- Fungsi Linear: Laju perubahan konstan. Grafik berupa garis lurus. Contoh: f(x) = mx + c, di mana m adalah gradien dan c adalah konstanta.
- Fungsi Non-Linear: Laju perubahan tidak konstan. Grafik berupa kurva. Contoh: f(x) = x², f(x) = x³, f(x) = √x.
Perbandingan Turunan Fungsi Aljabar dan Fungsi Trigonometri
Berikut tabel perbandingan antara turunan fungsi aljabar dan fungsi trigonometri. Tabel ini menunjukkan perbedaan rumus dan contoh turunan dari kedua jenis fungsi tersebut.
| Jenis Fungsi | Rumus Fungsi | Rumus Turunan | Contoh |
|---|---|---|---|
| Fungsi Aljabar (Polinomial) | f(x) = axn | f'(x) = naxn-1 | f(x) = 3x², f'(x) = 6x |
| Fungsi Trigonometri (Sinus) | f(x) = sin(x) | f'(x) = cos(x) | f(x) = sin(x), f'(x) = cos(x) |
| Fungsi Aljabar (Eksponensial) | f(x) = ex | f'(x) = ex | f(x) = ex, f'(x) = ex |
| Fungsi Trigonometri (Kosinus) | f(x) = cos(x) | f'(x) = -sin(x) | f(x) = cos(x), f'(x) = -sin(x) |
Ilustrasi Gradien Garis Singgung pada Kurva Fungsi Aljabar
Bayangkan sebuah kurva yang merepresentasikan fungsi aljabar. Gradien garis singgung pada suatu titik di kurva tersebut merupakan nilai turunan fungsi pada titik tersebut. Garis singgung menyentuh kurva hanya pada satu titik dan memberikan aproksimasi linier dari fungsi di sekitar titik tersebut. Semakin curam kemiringan garis singgung, semakin besar nilai absolut turunannya, menunjukkan laju perubahan fungsi yang lebih cepat di titik tersebut.
Jika garis singgung horizontal, maka turunannya bernilai nol, menunjukkan titik stasioner pada kurva.
Misalnya, jika kita memiliki kurva fungsi kuadrat f(x) = x², dan kita ingin mencari gradien garis singgung di titik x = 2, kita akan menghitung turunannya, f'(x) = 2x. Substitusikan x = 2, maka gradien garis singgung di titik tersebut adalah 4. Ini berarti garis singgung di titik (2,4) memiliki kemiringan 4.
Rumus dan Aturan Turunan Fungsi Aljabar
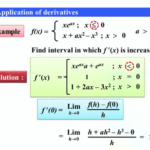
Turunan fungsi aljabar merupakan konsep fundamental dalam kalkulus. Memahami rumus dan aturan turunan sangat penting untuk menyelesaikan berbagai permasalahan matematika dan fisika, seperti menentukan kecepatan dan percepatan suatu objek, menentukan garis singgung kurva, dan mengoptimalkan fungsi.
Berikut ini akan dijelaskan beberapa rumus dasar turunan fungsi aljabar, beserta contoh penerapannya.
Rumus Turunan Dasar
Beberapa rumus dasar turunan fungsi aljabar yang perlu diingat adalah sebagai berikut:
- Turunan fungsi konstanta: Jika f(x) = c, dimana c adalah konstanta, maka f'(x) = 0.
- Turunan fungsi pangkat: Jika f(x) = x n, maka f'(x) = nx n-1.
- Turunan fungsi linear: Jika f(x) = ax + b, maka f'(x) = a.
Contoh penerapan:
- Jika f(x) = 5, maka f'(x) = 0.
- Jika f(x) = x3, maka f'(x) = 3x 2.
- Jika f(x) = 2x + 7, maka f'(x) = 2.
Aturan Perkalian
Aturan perkalian digunakan untuk mencari turunan dari perkalian dua fungsi. Jika f(x) = u(x)v(x), maka f'(x) = u'(x)v(x) + u(x)v'(x).
Contoh: Misalkan f(x) = (x 2 + 1)(x – 3). Maka u(x) = x 2 + 1 dan v(x) = x –
3. Dengan demikian:
f'(x) = (2x)(x – 3) + (x2 + 1)(1) = 2x 2
- 6x + x 2 + 1 = 3x 2
- 6x + 1
Aturan Pembagian
Aturan pembagian digunakan untuk mencari turunan dari pembagian dua fungsi. Jika f(x) = u(x)/v(x), maka f'(x) = [u'(x)v(x)
-u(x)v'(x)] / [v(x)] 2.
Contoh: Misalkan f(x) = (x 2 + 1) / (x – 2). Maka u(x) = x 2 + 1 dan v(x) = x –
2. Sehingga:
f'(x) = [(2x)(x – 2)
- (x2 + 1)(1)] / (x – 2) 2 = (2x 2
- 4x – x 2
- 1) / (x – 2) 2 = (x 2
- 4x – 1) / (x – 2) 2
Aturan Rantai, Contoh soal turunan fungsi aljabar
Aturan rantai digunakan untuk mencari turunan dari fungsi komposit (fungsi dalam fungsi). Jika f(x) = g(h(x)), maka f'(x) = g'(h(x))
– h'(x).
Contoh: Misalkan f(x) = (x 2 + 3) 4. Di sini, g(u) = u 4 dan h(x) = x 2 +
3. Maka:
f'(x) = 4(x2 + 3) 3
2x = 8x(x2 + 3) 3
Contoh Soal Turunan Fungsi Aljabar
Berikut contoh soal yang melibatkan fungsi pangkat, akar, dan pecahan, beserta penyelesaiannya:
- Tentukan turunan dari f(x) = √x + x3 – 5/x.
- Tentukan turunan dari f(x) = (x² + 2x) ⅓
Penyelesaian:
- f(x) = x1/2 + x 35x -1. Maka f'(x) = (1/2)x -1/2 + 3x 2 + 5x -2 = 1/(2√x) + 3x 2 + 5/x 2
- f(x) = (x² + 2x) ⅓. Dengan aturan rantai, f'(x) = ⅓(x² + 2x) -⅔
(2x + 2) = (2x + 2) / [3(x² + 2x)⅔]
Point-point Penting dalam Menghitung Turunan Fungsi Aljabar
- Pahami rumus dasar turunan fungsi aljabar.
- Kuasai aturan perkalian, pembagian, dan rantai.
- Latih dengan banyak soal untuk meningkatkan pemahaman.
- Perhatikan tanda positif dan negatif.
- Sederhanakan hasil turunan jika memungkinkan.
Penerapan Turunan Fungsi Aljabar dalam Menyelesaikan Masalah: Contoh Soal Turunan Fungsi Aljabar

Turunan fungsi aljabar memiliki aplikasi luas dalam memecahkan berbagai masalah dunia nyata. Konsep ini memungkinkan kita untuk menganalisis perubahan suatu besaran terhadap besaran lainnya, membantu dalam pengambilan keputusan yang optimal dalam berbagai bidang, mulai dari fisika dan teknik hingga ekonomi dan bisnis.
Pemahaman tentang turunan memungkinkan kita untuk menentukan laju perubahan, titik ekstrem (maksimum dan minimum), dan kelengkungan kurva. Dengan demikian, turunan menjadi alat yang ampuh untuk memodelkan dan menyelesaikan masalah yang melibatkan optimasi, laju perubahan, dan analisis perilaku fungsi.
Contoh Soal Cerita dan Penyelesaiannya
Berikut lima contoh soal cerita yang menunjukkan penerapan turunan fungsi aljabar dalam konteks permasalahan dunia nyata, beserta langkah-langkah penyelesaiannya secara detail.
- Soal: Sebuah bola dilempar vertikal ke atas dengan kecepatan awal 20 m/s. Tinggi bola setelah t detik dirumuskan sebagai h(t) = 20t – 5t². Tentukan kecepatan bola saat t = 2 detik dan kecepatan maksimum bola.
- Penyelesaian: Kecepatan adalah turunan pertama dari fungsi tinggi terhadap waktu. v(t) = h'(t) = 20 – 10t. Saat t = 2 detik, v(2) = 20 – 10(2) = 0 m/s. Kecepatan maksimum terjadi ketika v'(t) = -10 = 0, yang tidak mungkin. Kecepatan maksimum terjadi pada saat dilempar, yaitu 20 m/s.
- Soal: Sebuah perusahaan memproduksi x unit barang dengan biaya total C(x) = x³6x² + 15x + 100. Tentukan jumlah unit barang yang harus diproduksi agar biaya produksi minimum.
- Penyelesaian: Biaya minimum terjadi pada titik stasioner. C'(x) = 3x²
- 12x + 15 =
- Memecahkan persamaan kuadrat ini menghasilkan x =
- Untuk memastikan ini minimum, kita periksa turunan kedua: C”(x) = 6x – 12. C”(2) = 0, sehingga kita perlu analisis lebih lanjut (misalnya, uji garis bilangan). Analisis lebih lanjut menunjukkan bahwa x=2 merupakan titik minimum.
- Soal: Sebuah petani ingin memagari lahan berbentuk persegi panjang dengan luas 100 m². Berapa ukuran panjang dan lebar lahan agar panjang pagar minimum?
- Penyelesaian: Misalkan panjang = x dan lebar = y. Luas = xy = 100, sehingga y = 100/x. Panjang pagar P(x) = 2x + 2y = 2x + 200/x. P'(x) = 2 – 200/x² = 0. x = 10.
y = 10. P”(x) = 400/x³. P”(10) > 0, sehingga ini minimum.
- Soal: Sebuah roket diluncurkan vertikal ke atas dengan percepatan a(t) = 10 – t m/s². Kecepatan awal roket adalah 0 m/s. Tentukan kecepatan roket setelah 5 detik dan jarak yang ditempuh roket setelah 5 detik.
- Penyelesaian: Kecepatan v(t) adalah integral dari a(t): v(t) = 10t – (1/2)t² + C. Karena v(0) = 0, maka C = 0. v(5) = 10(5)
(1/2)(5)² = 37.5 m/s. Jarak s(t) adalah integral dari v(t)
s(t) = 5t²
- (1/6)t³ + D. Karena s(0) = 0, maka D = 0. s(5) = 5(5)²
- (1/6)(5)³ ≈ 104.17 m.
- Soal: Sebuah perusahaan menentukan fungsi permintaan untuk produknya adalah p(x) = 100 – 2x, dimana p adalah harga dan x adalah jumlah barang yang terjual. Tentukan jumlah barang yang harus dijual agar pendapatan maksimum.
- Penyelesaian: Pendapatan R(x) = xp(x) = x(100 – 2x) = 100x – 2x². R'(x) = 100 – 4x = 0. x = 25. R”(x) = -4 < 0, sehingga x = 25 merupakan titik maksimum.
Menentukan Titik Stasioner dan Jenisnya
Titik stasioner adalah titik di mana turunan pertama fungsi sama dengan nol (f'(x) = 0). Untuk menentukan jenis titik stasioner (maksimum, minimum, atau titik belok), kita perlu menganalisis turunan kedua.
- Jika f”(x) > 0, maka titik stasioner tersebut adalah minimum lokal.
- Jika f”(x) < 0, maka titik stasioner tersebut adalah maksimum lokal.
- Jika f”(x) = 0, maka diperlukan uji turunan tingkat tinggi atau uji garis bilangan untuk menentukan jenis titik stasioner.
Contoh Soal Penggunaan Turunan Kedua
Perhatikan contoh soal nomor 2 di atas. Penggunaan turunan kedua, C”(x) = 6x – 12, diperlukan untuk memastikan bahwa titik stasioner x = 2 merupakan titik minimum. Karena C”(2) = 0, uji lebih lanjut diperlukan untuk memastikan bahwa titik tersebut merupakan minimum.
Langkah-langkah umum dalam menyelesaikan masalah yang menggunakan turunan fungsi aljabar:
- Tentukan fungsi yang relevan dengan masalah.
- Tentukan turunan pertama fungsi tersebut.
- Cari titik stasioner dengan menyelesaikan f'(x) = 0.
- Tentukan jenis titik stasioner menggunakan turunan kedua (f”(x)) atau uji garis bilangan.
- Interpretasikan hasil dalam konteks masalah.
Contoh Soal Turunan Fungsi Aljabar Tingkat Lanjut
Setelah memahami konsep dasar turunan fungsi aljabar, mari kita berlatih dengan soal-soal yang lebih kompleks. Soal-soal berikut akan menguji pemahaman Anda tentang turunan fungsi komposisi, fungsi implisit, dan fungsi yang melibatkan logaritma serta eksponen. Penyelesaian setiap soal akan diuraikan secara detail agar Anda dapat memahami langkah-langkahnya dengan baik.
Contoh Soal Turunan Fungsi Komposisi
Fungsi komposisi melibatkan penggabungan dua atau lebih fungsi. Mencari turunannya memerlukan pemahaman aturan rantai. Berikut tiga contoh soal beserta penyelesaiannya:
- Misalkan f(x) = (2x² + 3x)4. Tentukan f'(x).
- Diketahui g(x) = sin(e x). Tentukan g'(x).
- Jika h(x) = ln(x² + 1), tentukan h'(x).
Penyelesaian:
- Untuk f(x) = (2x² + 3x)4, kita gunakan aturan rantai. Misalkan u = 2x² + 3x, maka f(x) = u 4. Turunannya adalah f'(x) = 4u³
u’ = 4(2x² + 3x)³(4x + 3).
- Untuk g(x) = sin(e x), kita gunakan aturan rantai dua kali. Misalkan u = e x, maka g(x) = sin(u). Turunannya adalah g'(x) = cos(u)
- u’ = cos(e x)
- e x.
- Untuk h(x) = ln(x² + 1), kita gunakan aturan rantai. Misalkan u = x² + 1, maka h(x) = ln(u). Turunannya adalah h'(x) = (1/u)
- u’ = (1/(x² + 1))
- 2x = 2x/(x² + 1).
Contoh Soal Turunan Fungsi Implisit
Fungsi implisit adalah fungsi yang tidak dinyatakan dalam bentuk y = f(x). Untuk mencari turunannya, kita perlu melakukan diferensiasi implisit.
Contoh: Tentukan dy/dx dari persamaan x² + y² = 25.
Penyelesaian: Kita diferensialkan kedua ruas persamaan terhadap x:
2x + 2y(dy/dx) = 0
Kemudian selesaikan untuk dy/dx:
2y(dy/dx) = -2x
dy/dx = -x/y
Contoh Soal Turunan Fungsi dengan Logaritma dan Eksponen
Turunan fungsi yang melibatkan logaritma dan eksponen memerlukan pemahaman sifat-sifat logaritma dan aturan turunan eksponensial. Langkah-langkah penyelesaiannya seringkali melibatkan kombinasi aturan rantai dan sifat logaritma.
Contoh: Tentukan turunan dari f(x) = x x.
Penyelesaian: Untuk menyelesaikan soal ini, kita dapat menggunakan logaritma natural. Pertama, kita ambil logaritma natural dari kedua ruas:
ln(f(x)) = ln(xx) = x ln(x)
Kemudian, kita diferensialkan kedua ruas terhadap x menggunakan aturan rantai dan aturan perkalian:
(1/f(x))
f'(x) = ln(x) + x(1/x) = ln(x) + 1
Selanjutnya, kita selesaikan untuk f'(x):
f'(x) = f(x)(ln(x) + 1) = xx (ln(x) + 1)
Ringkasan Penutup
Memahami turunan fungsi aljabar bukan hanya sekedar menghafal rumus, melainkan memahami konsep dan aplikasinya. Dengan latihan yang cukup dan pemahaman yang mendalam, Anda akan mampu menyelesaikan berbagai soal turunan, bahkan yang tingkat lanjut sekalipun. Kemampuan ini akan sangat berguna dalam berbagai bidang studi dan aplikasi di dunia nyata, seperti fisika, ekonomi, dan teknik.

