- Pengertian Tabel Distribusi Frekuensi: Contoh Tabel Distribusi Frekuensi
-
Cara Membuat Tabel Distribusi Frekuensi
- Langkah-langkah Membuat Tabel Distribusi Frekuensi untuk Data Tunggal dan Kelompok
- Contoh Perhitungan Frekuensi Kumulatif dan Frekuensi Relatif
- Menentukan Rentang Kelas dan Banyak Kelas
- Langkah-langkah Membuat Tabel Distribusi Frekuensi untuk Data Kualitatif
- Contoh Tabel Distribusi Frekuensi Berat Badan Bayi dengan Rentang Kelas Berbeda
-
Tabel Distribusi Frekuensi
- Perbedaan Tabel Distribusi Frekuensi Data Tunggal dan Data Kelompok
- Contoh Tabel Distribusi Frekuensi untuk Data Nominal dan Data Ordinal
- Contoh Tabel Distribusi Frekuensi untuk Data Interval dan Rasio
- Perbandingan Tabel Distribusi Frekuensi Data Diskrit dan Data Kontinu
- Penggunaan Tabel Distribusi Frekuensi dalam Berbagai Bidang
- Interpretasi Tabel Distribusi Frekuensi
- Terakhir
Contoh tabel distribusi frekuensi merupakan alat penting dalam statistik deskriptif untuk menyajikan data secara ringkas dan informatif. Tabel ini membantu kita memahami pola dan tren dalam data mentah yang kompleks, memudahkan interpretasi dan analisis lebih lanjut. Baik dalam penelitian ilmiah, analisis bisnis, maupun kehidupan sehari-hari, memahami dan menggunakan tabel distribusi frekuensi sangatlah krusial untuk mengambil keputusan yang tepat berdasarkan data.
Artikel ini akan membahas secara komprehensif berbagai aspek terkait tabel distribusi frekuensi, mulai dari pengertian dasar, cara pembuatan untuk berbagai jenis data, hingga interpretasi hasilnya. Dengan contoh-contoh konkret dan penjelasan langkah demi langkah, diharapkan pembaca dapat dengan mudah memahami dan menerapkan konsep ini dalam berbagai konteks.
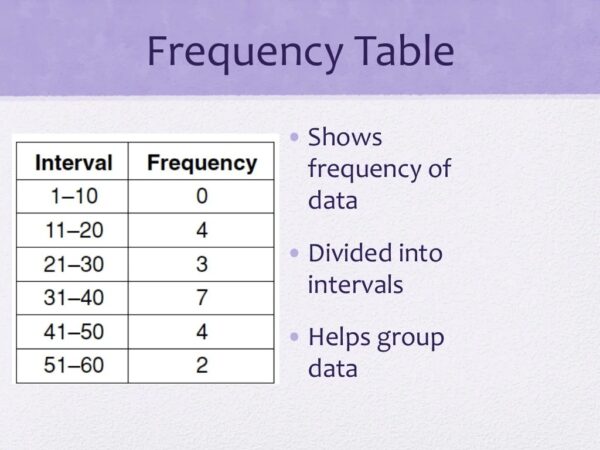
Pengertian Tabel Distribusi Frekuensi: Contoh Tabel Distribusi Frekuensi
Tabel distribusi frekuensi merupakan alat penting dalam statistika yang digunakan untuk menyusun dan menyajikan data dalam bentuk yang lebih mudah dipahami dan diinterpretasi. Tabel ini mengelompokkan data mentah menjadi beberapa kelas interval, kemudian menghitung frekuensi kemunculan data dalam setiap kelas tersebut. Dengan demikian, kita dapat melihat pola dan tren dalam data dengan lebih jelas.
Penggunaan tabel distribusi frekuensi memungkinkan kita untuk merangkum data yang besar dan kompleks menjadi representasi yang lebih ringkas dan informatif. Hal ini sangat berguna untuk menganalisis data, mengidentifikasi pola, dan mengambil kesimpulan yang bermakna.
Contoh Kasus Penggunaan Tabel Distribusi Frekuensi
Tabel distribusi frekuensi memiliki aplikasi yang luas dalam berbagai bidang. Misalnya, dalam dunia pendidikan, tabel ini dapat digunakan untuk menganalisis nilai ujian siswa. Dengan mengelompokkan nilai-nilai tersebut ke dalam interval tertentu (misalnya, 0-59, 60-69, 70-79, dan seterusnya), kita dapat melihat sebaran nilai ujian dan mengidentifikasi proporsi siswa yang berada di setiap rentang nilai tersebut. Contoh lain adalah dalam riset pasar, di mana tabel distribusi frekuensi dapat digunakan untuk menganalisis preferensi konsumen terhadap suatu produk berdasarkan demografi, harga, atau fitur produk.
Perbedaan Data Kualitatif dan Kuantitatif
Sebelum membahas lebih lanjut, penting untuk memahami perbedaan antara data kualitatif dan kuantitatif, karena jenis data ini menentukan bagaimana tabel distribusi frekuensi disusun dan diinterpretasikan.
| Jenis Data | Contoh |
|---|---|
| Kualitatif (Deskriptif) | Warna rambut (hitam, pirang, cokelat), jenis kelamin (laki-laki, perempuan), merek mobil kesukaan |
| Kuantitatif (Numerik) | Tinggi badan (dalam cm), berat badan (dalam kg), nilai ujian (dalam angka) |
Contoh Tabel Distribusi Frekuensi: Tinggi Badan Siswa
Misalkan kita memiliki data tinggi badan 20 siswa (dalam cm): 160, 165, 170, 170, 172, 175, 175, 175, 178, 180, 180, 182, 185, 185, 185, 190, 190, 192, 195,
200. Kita dapat menyusun tabel distribusi frekuensi sebagai berikut (dengan interval kelas 10 cm):
| Interval Tinggi Badan (cm) | Frekuensi |
|---|---|
| 160-169 | 2 |
| 170-179 | 6 |
| 180-189 | 6 |
| 190-199 | 4 |
| 200-209 | 2 |
Dari tabel di atas, terlihat bahwa sebagian besar siswa memiliki tinggi badan antara 170-189 cm. Sebaran data cukup merata, meskipun terdapat sedikit kecenderungan ke arah tinggi badan yang lebih tinggi.
Jenis Data yang Cocok untuk Tabel Distribusi Frekuensi
Tabel distribusi frekuensi paling cocok untuk data kuantitatif, terutama data yang memiliki banyak nilai dan rentang yang luas. Data kualitatif juga dapat disajikan dalam tabel frekuensi, tetapi biasanya dalam bentuk kategorisasi sederhana, tanpa interval kelas. Data yang memiliki jumlah nilai yang sedikit, tidak perlu disajikan dalam tabel distribusi frekuensi karena akan kurang efektif.
Cara Membuat Tabel Distribusi Frekuensi
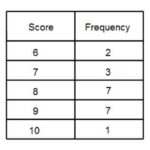
Tabel distribusi frekuensi merupakan alat penting dalam statistika deskriptif yang digunakan untuk menyusun dan merangkum data mentah menjadi bentuk yang lebih mudah dipahami dan diinterpretasi. Tabel ini mengelompokkan data ke dalam kelas-kelas interval tertentu, menunjukkan berapa banyak data yang jatuh ke dalam setiap kelas tersebut. Pembuatan tabel ini berbeda tergantung pada jenis data yang dihadapi, yaitu data tunggal atau data kelompok, serta data kualitatif atau kuantitatif.
Langkah-langkah Membuat Tabel Distribusi Frekuensi untuk Data Tunggal dan Kelompok
Langkah-langkah pembuatan tabel distribusi frekuensi sedikit berbeda antara data tunggal dan data kelompok. Data tunggal merupakan data yang tidak dikelompokkan, sedangkan data kelompok sudah dikelompokkan ke dalam interval tertentu. Berikut uraiannya:
- Data Tunggal: Hitung frekuensi setiap nilai data. Buat tabel dengan kolom nilai data dan frekuensi. Kemudian, hitung frekuensi kumulatif dan frekuensi relatif.
- Data Kelompok: Tentukan rentang data (range), yaitu selisih antara nilai terbesar dan terkecil. Tentukan jumlah kelas (k) yang sesuai, misalnya menggunakan aturan Sturges (k = 1 + 3.322 log n, dengan n adalah jumlah data). Hitung lebar kelas (i) dengan membagi rentang data dengan jumlah kelas (i = range/k). Buat tabel dengan kolom batas bawah kelas, batas atas kelas, titik tengah kelas, frekuensi, frekuensi kumulatif, dan frekuensi relatif.
Masukkan data ke dalam kelas yang sesuai dan hitung frekuensi masing-masing kelas.
Contoh Perhitungan Frekuensi Kumulatif dan Frekuensi Relatif
Misalnya, nilai ujian 20 siswa adalah: 70, 80, 85, 90, 75, 80, 85, 95, 70, 85, 90, 75, 80, 90, 85, 75, 95, 80, 90,
85. Kita dapat membuat tabel distribusi frekuensi sebagai berikut:
| Nilai Ujian | Frekuensi (f) | Frekuensi Kumulatif (fk) | Frekuensi Relatif (fr) |
|---|---|---|---|
| 70 | 2 | 2 | 0.1 |
| 75 | 3 | 5 | 0.15 |
| 80 | 4 | 9 | 0.2 |
| 85 | 4 | 13 | 0.2 |
| 90 | 4 | 17 | 0.2 |
| 95 | 2 | 19 | 0.1 |
| Total | 20 | 1.0 |
Frekuensi kumulatif adalah jumlah frekuensi hingga kelas tertentu. Frekuensi relatif adalah proporsi frekuensi suatu kelas terhadap total frekuensi.
Menentukan Rentang Kelas dan Banyak Kelas
Menentukan rentang kelas dan banyak kelas sangat penting untuk membuat tabel distribusi frekuensi yang informatif. Rentang kelas ditentukan dengan menghitung selisih antara nilai data terbesar dan terkecil. Banyak kelas dapat ditentukan menggunakan aturan Sturges atau dengan pertimbangan lain, seperti kemudahan interpretasi dan visualisasi data. Tujuannya adalah untuk menciptakan kelas-kelas yang mewakili data secara merata dan menghindari kelas yang terlalu banyak atau terlalu sedikit.
Langkah-langkah Membuat Tabel Distribusi Frekuensi untuk Data Kualitatif
Untuk data kualitatif, langkah-langkahnya lebih sederhana. Data kualitatif bersifat kategorikal, bukan numerik.
- Identifikasi kategori-kategori yang ada dalam data.
- Hitung frekuensi setiap kategori.
- Buat tabel dengan kolom kategori dan frekuensi.
Contoh: Misalnya data tentang warna mobil yang terparkir di suatu tempat parkir. Kategori-kategorinya bisa berupa merah, biru, hitam, putih, dll. Hitunglah berapa banyak mobil dengan masing-masing warna.
Contoh Tabel Distribusi Frekuensi Berat Badan Bayi dengan Rentang Kelas Berbeda
Berikut contoh tabel distribusi frekuensi berat badan bayi (dalam kg) dengan dua rentang kelas yang berbeda. Perbedaan rentang kelas akan mempengaruhi interpretasi data.
Contoh 1: Rentang kelas 0.5 kg
| Berat Badan (kg) | Frekuensi |
|---|---|
| 2.0 – 2.5 | 5 |
| 2.5 – 3.0 | 10 |
| 3.0 – 3.5 | 15 |
| 3.5 – 4.0 | 8 |
| 4.0 – 4.5 | 2 |
Contoh 2: Rentang kelas 1.0 kg
| Berat Badan (kg) | Frekuensi |
|---|---|
| 2.0 – 3.0 | 15 |
| 3.0 – 4.0 | 23 |
| 4.0 – 5.0 | 2 |
Perbandingan: Dengan rentang kelas yang lebih kecil (0.5 kg), kita mendapatkan gambaran yang lebih detail tentang distribusi berat badan bayi. Namun, dengan rentang kelas yang lebih besar (1.0 kg), tabel menjadi lebih ringkas tetapi detailnya berkurang.
Tabel Distribusi Frekuensi
Tabel distribusi frekuensi merupakan alat penting dalam statistika yang digunakan untuk menyusun dan menyajikan data mentah agar lebih mudah dipahami dan diinterpretasi. Tabel ini mengelompokkan data berdasarkan nilai atau rentang nilai tertentu, serta menunjukkan berapa kali setiap nilai atau rentang nilai tersebut muncul (frekuensi). Pemahaman yang baik tentang jenis-jenis tabel distribusi frekuensi sangat krusial untuk analisis data yang efektif.
Perbedaan Tabel Distribusi Frekuensi Data Tunggal dan Data Kelompok
Perbedaan utama terletak pada bagaimana data disajikan. Tabel distribusi frekuensi data tunggal menampilkan frekuensi setiap nilai data yang unik. Sementara itu, tabel distribusi frekuensi data kelompok mengelompokkan data ke dalam interval kelas tertentu, lalu menampilkan frekuensi untuk setiap interval tersebut. Data tunggal cocok untuk data dengan jumlah nilai unik yang sedikit, sedangkan data kelompok lebih efisien untuk data dengan banyak nilai unik atau data kontinu.
Contoh Tabel Distribusi Frekuensi untuk Data Nominal dan Data Ordinal
Data nominal mewakili kategori tanpa urutan tertentu, sedangkan data ordinal memiliki urutan peringkat. Oleh karena itu, penyajian tabel distribusi frekuensi untuk kedua jenis data ini berbeda dalam hal interpretasi.
Contoh Data Nominal (Warna Kesukaan):
| Warna | Frekuensi |
|---|---|
| Merah | 15 |
| Biru | 10 |
| Hijau | 8 |
| Kuning | 7 |
Contoh Data Ordinal (Tingkat Kepuasan Pelanggan):
| Tingkat Kepuasan | Frekuensi |
|---|---|
| Sangat Puas | 20 |
| Puas | 15 |
| Netral | 5 |
| Tidak Puas | 2 |
Contoh Tabel Distribusi Frekuensi untuk Data Interval dan Rasio
Data interval memiliki jarak yang sama antara nilai-nilai berurutan, tetapi tidak memiliki titik nol absolut. Data rasio memiliki jarak yang sama dan titik nol absolut. Contoh tabel distribusi frekuensi untuk data ini seringkali menggunakan data kelompok.
Contoh Data Interval (Suhu):
| Rentang Suhu (°C) | Frekuensi |
|---|---|
| 20-25 | 12 |
| 26-31 | 18 |
| 32-37 | 10 |
Contoh Data Rasio (Pendapatan):
| Rentang Pendapatan (Rp) | Frekuensi |
|---|---|
| 0-10.000.000 | 5 |
| 10.000.001-20.000.000 | 15 |
| 20.000.001-30.000.000 | 10 |
Perbandingan Tabel Distribusi Frekuensi Data Diskrit dan Data Kontinu
Data diskrit hanya dapat memiliki nilai-nilai tertentu (misalnya, jumlah mobil), sedangkan data kontinu dapat memiliki nilai apa pun dalam rentang tertentu (misalnya, tinggi badan). Perbedaan ini memengaruhi cara data dikelompokkan dalam tabel distribusi frekuensi.
| Karakteristik | Data Diskrit | Data Kontinu |
|---|---|---|
| Nilai Data | Terpisah dan terhitung | Berkesinambungan |
| Pengelompokan | Biasanya tidak perlu pengelompokan jika jumlah nilai sedikit | Seringkali memerlukan pengelompokan ke dalam interval kelas |
| Contoh | Jumlah anak dalam keluarga | Tinggi badan siswa |
Penggunaan Tabel Distribusi Frekuensi dalam Berbagai Bidang
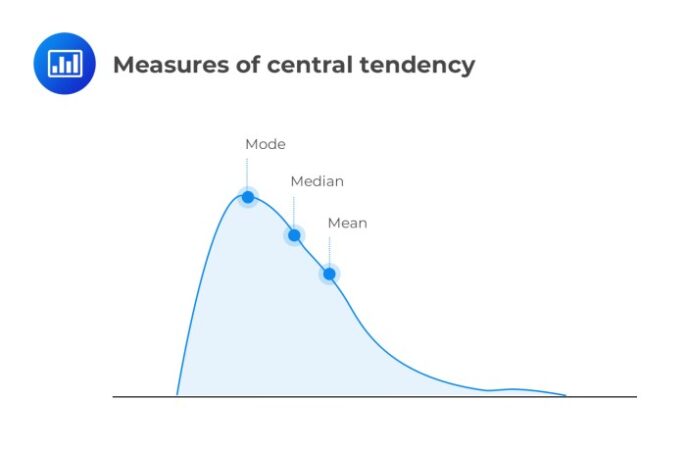
Tabel distribusi frekuensi memiliki aplikasi luas di berbagai disiplin ilmu. Dalam statistik, tabel ini mendasari berbagai analisis seperti perhitungan rata-rata, median, dan modus. Di riset pasar, tabel ini membantu menganalisis preferensi konsumen dan pola pembelian. Di ilmu sosial, tabel ini digunakan untuk menganalisis data demografis, sikap, dan perilaku sosial.
Interpretasi Tabel Distribusi Frekuensi
Tabel distribusi frekuensi merupakan alat visual yang efektif untuk memahami pola dan tren dalam suatu kumpulan data. Setelah tabel distribusi frekuensi disusun, langkah selanjutnya adalah menginterpretasi informasi yang terkandung di dalamnya. Interpretasi ini akan membantu kita untuk mengambil kesimpulan dan membuat keputusan yang lebih tepat berdasarkan data yang ada.
Interpretasi tabel distribusi frekuensi melibatkan analisis berbagai aspek, mulai dari frekuensi masing-masing kelas interval hingga identifikasi pola persebaran data. Pemahaman yang mendalam tentang interpretasi ini sangat krusial untuk mengolah data mentah menjadi informasi yang bermakna dan berguna.
Interpretasi Informasi dalam Tabel Distribusi Frekuensi
Interpretasi tabel distribusi frekuensi dimulai dengan memahami arti dari setiap komponen tabel, yaitu kelas interval, frekuensi, frekuensi relatif, dan frekuensi kumulatif. Dengan memahami masing-masing komponen tersebut, kita dapat menganalisis data dengan lebih mudah dan akurat. Misalnya, frekuensi menunjukkan jumlah data yang berada dalam setiap kelas interval, sementara frekuensi relatif menunjukkan proporsi data dalam setiap kelas interval terhadap total data.
Kita dapat membandingkan frekuensi antar kelas interval untuk mengidentifikasi kelas interval mana yang memiliki frekuensi paling tinggi (modus) dan kelas interval mana yang memiliki frekuensi paling rendah. Informasi ini memberikan gambaran awal tentang persebaran data.
Contoh Interpretasi Tabel Distribusi Frekuensi Penjualan Produk
Misalkan kita memiliki data penjualan produk A selama 100 hari. Setelah diolah, data tersebut menghasilkan tabel distribusi frekuensi sebagai berikut:
| Kelas Interval (Unit Terjual) | Frekuensi | Frekuensi Relatif |
|---|---|---|
| 0-10 | 10 | 0.1 |
| 11-20 | 25 | 0.25 |
| 21-30 | 30 | 0.3 |
| 31-40 | 20 | 0.2 |
| 41-50 | 15 | 0.15 |
Dari tabel tersebut, terlihat bahwa kelas interval 21-30 memiliki frekuensi tertinggi (30 unit), yang menunjukkan bahwa penjualan produk A paling banyak berada di rentang tersebut. Frekuensi relatif menunjukkan bahwa 30% dari total penjualan berada pada rentang 21-30 unit.
Penggunaan Tabel Distribusi Frekuensi untuk Pengambilan Keputusan
Informasi dari tabel distribusi frekuensi dapat digunakan untuk berbagai macam pengambilan keputusan. Contohnya, dalam kasus penjualan produk A di atas, manajemen dapat menggunakan informasi tersebut untuk menentukan strategi pemasaran yang tepat. Melihat tingginya penjualan pada rentang 21-30 unit, perusahaan dapat fokus pada strategi untuk meningkatkan penjualan di rentang tersebut atau mempertimbangkan untuk menawarkan paket penjualan yang lebih menarik di rentang tersebut.
Identifikasi Pola dan Tren dari Data
Dengan mengamati frekuensi dan frekuensi relatif pada setiap kelas interval, kita dapat mengidentifikasi pola dan tren dalam data. Misalnya, jika frekuensi meningkat secara konsisten dari kelas interval terendah ke kelas interval tertinggi, ini menunjukkan tren peningkatan penjualan. Sebaliknya, jika frekuensi menurun secara konsisten, ini menunjukkan tren penurunan penjualan. Pola yang lebih kompleks juga dapat diidentifikasi, seperti adanya pola siklis atau musiman.
Analisis Persebaran Data
Tabel distribusi frekuensi memungkinkan kita untuk menganalisis persebaran data. Kita dapat melihat apakah data terdistribusi secara simetris, miring ke kanan (positif), atau miring ke kiri (negatif). Persebaran data yang simetris menunjukkan bahwa data tersebar merata di sekitar nilai tengah. Persebaran data yang miring ke kanan menunjukkan bahwa sebagian besar data terkonsentrasi pada nilai yang lebih rendah, sedangkan persebaran data yang miring ke kiri menunjukkan bahwa sebagian besar data terkonsentrasi pada nilai yang lebih tinggi.
Berdasarkan tabel distribusi frekuensi penjualan produk A, terlihat bahwa data cenderung simetris, meskipun sedikit miring ke kanan. Hal ini menunjukkan bahwa penjualan produk A relatif stabil, dengan sebagian besar penjualan berkisar di sekitar rata-rata.
Terakhir
Memahami dan mampu membuat tabel distribusi frekuensi merupakan keterampilan fundamental dalam analisis data. Kemampuan ini memungkinkan kita untuk menyederhanakan data kompleks, mengidentifikasi pola, dan mengambil kesimpulan yang bermakna. Dengan pemahaman yang mendalam tentang berbagai jenis data dan langkah-langkah pembuatan tabel, kita dapat memanfaatkan alat ini untuk berbagai keperluan, mulai dari riset sederhana hingga analisis data skala besar. Semoga panduan ini memberikan pemahaman yang komprehensif dan bermanfaat bagi pembaca.