- Struktur Jaring-Jaring Balok
- Rumus dan Perhitungan Jaring-Jaring Balok: Jaring Jaring Balok Beserta Alas Dan Tutupnya
- Penerapan Jaring-Jaring Balok dalam Kehidupan Sehari-hari
-
Variasi Jaring-Jaring Balok
- Kemungkinan Variasi Bentuk Jaring-Jaring Balok
- Contoh Jaring-Jaring Balok Tidak Konvensional
- Ilustrasi Jaring-Jaring Balok dengan Alas dan Tutup Berbentuk Segitiga
- Perbedaan dan Persamaan Jaring-Jaring Balok Berbagai Bentuk
- Langkah-Langkah Membuat Jaring-Jaring Balok dengan Alas dan Tutup Berbentuk Trapesium
- Penutupan Akhir
Jaring jaring balok beserta alas dan tutupnya – Jaring-jaring balok beserta alas dan tutupnya merupakan konsep geometri ruang yang fundamental. Memahami jaring-jaring ini bukan hanya penting untuk pelajaran matematika, tetapi juga bermanfaat dalam berbagai aspek kehidupan sehari-hari, mulai dari merancang kemasan hingga membangun konstruksi. Bentuk jaring-jaring balok sendiri beragam, bergantung pada ukuran dan bentuk alas serta tutupnya, yang bisa berupa persegi, persegi panjang, atau bahkan bangun datar lainnya.
Mari kita jelajahi lebih dalam dunia jaring-jaring balok yang menarik ini.
Artikel ini akan membahas berbagai konfigurasi jaring-jaring balok, termasuk perbedaan antara balok persegi dan balok persegi panjang. Kita akan mempelajari cara menghitung luas permukaan dan volume balok, serta melihat penerapan konsep ini dalam kehidupan nyata. Selain itu, akan dibahas juga variasi jaring-jaring balok dengan bentuk alas dan tutup yang tidak konvensional.
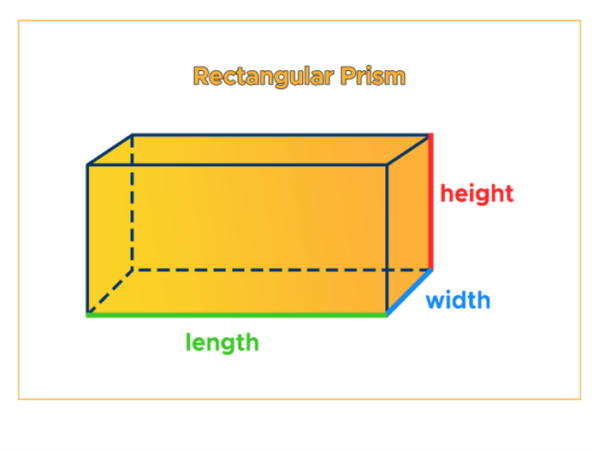
Struktur Jaring-Jaring Balok

Jaring-jaring balok merupakan representasi dua dimensi dari bangun ruang tiga dimensi, yaitu balok. Memahami jaring-jaring balok sangat penting untuk memahami sifat-sifat geometri balok dan memudahkan dalam menghitung luas permukaan dan volume. Berbagai konfigurasi jaring-jaring balok memungkinkan pemahaman yang lebih komprehensif tentang bangun ruang ini.
Konfigurasi Jaring-Jaring Balok
Terdapat beberapa konfigurasi jaring-jaring balok, bergantung pada ukuran dan bentuk baloknya. Perbedaan utama terletak pada bentuk alas dan tutup balok, apakah persegi atau persegi panjang. Balok persegi memiliki alas dan tutup berbentuk persegi, sementara balok persegi panjang memiliki alas dan tutup berbentuk persegi panjang. Konfigurasi jaring-jaringnya pun akan berbeda, meskipun jumlah sisi tetap sama.
Perbedaan lain terletak pada kesamaan atau perbedaan ukuran alas dan tutup. Pada balok kubus, misalnya, semua sisi berbentuk persegi dan ukurannya sama. Namun, pada balok non-kubus, ukuran alas dan tutup bisa berbeda, menghasilkan berbagai kemungkinan konfigurasi jaring-jaring.
Ilustrasi Jaring-Jaring Balok
Berikut ilustrasi jaring-jaring balok kubus dan balok non-kubus:
Jaring-jaring Balok Kubus (misal, sisi 5 cm): Bayangkan enam persegi identik dengan sisi 5 cm tersusun berdampingan. Empat persegi membentuk baris tengah, dengan dua persegi tersusun di atas dan di bawah baris tersebut. Setiap persegi mewakili sisi balok kubus.
Jaring-jaring Balok Non-Kubus (misal, alas 6 cm x 4 cm, tinggi 3 cm): Bayangkan dua persegi panjang dengan ukuran 6 cm x 4 cm (alas dan tutup). Empat persegi panjang lainnya, masing-masing berukuran 6 cm x 3 cm dan 4 cm x 3 cm, akan menghubungkan alas dan tutup. Susunannya dapat bervariasi, tetapi selalu melibatkan dua persegi panjang yang sama sebagai alas dan tutup.
Elemen-Elemen Penting Jaring-Jaring Balok
Jaring-jaring balok terdiri dari beberapa elemen penting yang perlu dipahami. Pemahaman tentang elemen-elemen ini memudahkan dalam analisis dan perhitungan geometri balok.
- Sisi: Permukaan datar yang membatasi balok. Pada balok, terdapat enam sisi.
- Rusuk: Garis yang merupakan pertemuan dua sisi. Balok memiliki 12 rusuk.
- Titik Sudut: Titik pertemuan tiga rusuk. Balok memiliki 8 titik sudut.
Perbandingan Karakteristik Jaring-Jaring Balok
Tabel berikut membandingkan karakteristik jaring-jaring balok dengan berbagai ukuran alas dan tutup.
| Ukuran Alas | Ukuran Tutup | Tinggi | Jumlah Sisi |
|---|---|---|---|
| 5 cm x 5 cm | 5 cm x 5 cm | 5 cm | 6 |
| 6 cm x 4 cm | 6 cm x 4 cm | 3 cm | 6 |
| 8 cm x 6 cm | 8 cm x 6 cm | 5 cm | 6 |
| 10 cm x 5 cm | 10 cm x 5 cm | 7 cm | 6 |
Rumus dan Perhitungan Jaring-Jaring Balok: Jaring Jaring Balok Beserta Alas Dan Tutupnya
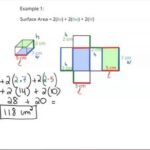
Memahami rumus dan perhitungan untuk jaring-jaring balok sangat penting dalam berbagai aplikasi, mulai dari desain konstruksi hingga pembuatan kemasan. Kemampuan menghitung luas permukaan dan volume balok memungkinkan kita untuk menentukan jumlah material yang dibutuhkan atau kapasitas penyimpanan suatu wadah.
Rumus Luas Permukaan Jaring-Jaring Balok
Luas permukaan jaring-jaring balok merupakan total luas semua sisi penyusunnya. Rumus untuk menghitung luas permukaan balok adalah:
Luas Permukaan = 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi)
Rumus ini didapat dari penjumlahan luas keenam sisi balok, yaitu dua sisi dengan ukuran panjang x lebar, dua sisi dengan ukuran panjang x tinggi, dan dua sisi dengan ukuran lebar x tinggi.
Rumus Volume Balok, Jaring jaring balok beserta alas dan tutupnya
Volume balok menyatakan kapasitas ruang yang dapat ditempati di dalam balok. Rumusnya sangat sederhana dan mudah diingat:
Volume = panjang x lebar x tinggi
Rumus ini didapatkan dari perkalian ketiga dimensi balok, yaitu panjang, lebar, dan tinggi.
Contoh Perhitungan Luas Permukaan dan Volume Balok
Mari kita selesaikan contoh soal berikut. Misalkan sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 3 cm.
Luas Permukaan:
Luas Permukaan = 2 x (10 cm x 5 cm + 10 cm x 3 cm + 5 cm x 3 cm) = 2 x (50 cm² + 30 cm² + 15 cm²) = 2 x 95 cm² = 190 cm²
Volume:
Volume = 10 cm x 5 cm x 3 cm = 150 cm³
Jadi, luas permukaan balok adalah 190 cm² dan volumenya adalah 150 cm³.
Contoh Soal Cerita dan Penyelesaiannya
Seorang petani ingin membuat kotak penyimpanan hasil panen berupa balok dengan panjang 1,5 meter, lebar 1 meter, dan tinggi 0,8 meter. Berapa luas permukaan kayu yang dibutuhkan untuk membuat kotak tersebut? Berapa volume hasil panen maksimal yang dapat disimpan dalam kotak tersebut?
- Menentukan ukuran balok: Panjang = 1,5 m, Lebar = 1 m, Tinggi = 0,8 m
- Menghitung luas permukaan: Luas Permukaan = 2 x (1,5 m x 1 m + 1,5 m x 0,8 m + 1 m x 0,8 m) = 2 x (1,5 m² + 1,2 m² + 0,8 m²) = 2 x 3,5 m² = 7 m²
- Menghitung volume: Volume = 1,5 m x 1 m x 0,8 m = 1,2 m³
- Kesimpulan: Petani membutuhkan 7 m² kayu untuk membuat kotak dan kotak tersebut dapat menyimpan hasil panen maksimal 1,2 m³.
Penerapan Jaring-Jaring Balok dalam Kehidupan Sehari-hari
Pemahaman tentang jaring-jaring balok bukan hanya sekadar materi pelajaran geometri. Konsep ini memiliki aplikasi praktis yang luas dalam kehidupan sehari-hari, berperan penting dalam pembuatan dan desain berbagai benda di sekitar kita. Memahami jaring-jaring balok memungkinkan kita untuk memvisualisasikan bentuk tiga dimensi dari pola dua dimensi, sehingga memudahkan proses pembuatan dan perakitan.
Contoh Benda Berbentuk Balok
Banyak benda di sekitar kita berbentuk balok, mulai dari yang sederhana hingga yang kompleks. Bentuk balok dipilih karena efisiensi dan kestabilannya. Perhatikanlah kotak sepatu, buku, bata, dan bahkan beberapa jenis bangunan. Semua benda tersebut memiliki karakteristik bentuk balok yang dapat diuraikan melalui jaring-jaringnya.
Peran Jaring-Jaring Balok dalam Pembuatan Benda
Pemahaman jaring-jaring balok sangat krusial dalam proses pembuatan berbagai benda. Misalnya, dalam pembuatan kotak kardus, desain jaring-jaring memastikan semua sisi terhubung dengan tepat dan menghasilkan kotak yang kokoh. Begitu pula dalam pembuatan kemasan produk, desain jaring-jaring yang efisien dapat meminimalkan penggunaan material dan meningkatkan efisiensi produksi. Pada industri furnitur, desain jaring-jaring balok digunakan untuk merancang dan membuat lemari, meja, dan rak dengan ukuran dan bentuk yang diinginkan.
Penerapan Jaring-Jaring Balok dalam Arsitektur dan Konstruksi
Dalam bidang arsitektur dan konstruksi, pemahaman jaring-jaring balok berperan penting dalam perencanaan dan pembangunan bangunan. Desain struktur bangunan, khususnya yang melibatkan elemen balok seperti kolom dan dinding, seringkali dimulai dengan pembuatan model tiga dimensi yang kemudian diuraikan menjadi jaring-jaring dua dimensi untuk memudahkan proses fabrikasi dan perakitan. Misalnya, perencanaan sebuah gedung bertingkat tinggi melibatkan perhitungan yang rumit untuk memastikan stabilitas struktur.
Jaring-jaring balok membantu dalam memvisualisasikan dan menganalisis interaksi antara berbagai komponen struktur.
Sebagai contoh, perencanaan konstruksi sebuah gudang penyimpanan yang berbentuk balok besar, akan diawali dengan perancangan jaring-jaring balok yang mendetail. Jaring-jaring ini akan menunjukan ukuran setiap dinding, atap, dan lantai, serta bagaimana bagian-bagian tersebut akan disusun dan dihubungkan. Hal ini memastikan efisiensi material dan kekuatan struktur gudang tersebut.
Manfaat Memahami Jaring-Jaring Balok dalam Pemecahan Masalah
Kemampuan memvisualisasikan dan menguraikan bentuk tiga dimensi menjadi jaring-jaring dua dimensi sangat membantu dalam menyelesaikan berbagai masalah praktis. Misalnya, dalam mengemas barang-barang untuk pengiriman, memahami jaring-jaring balok dapat membantu menentukan ukuran kotak yang paling efisien untuk meminimalkan ruang kosong dan biaya pengiriman. Atau, dalam merancang sebuah rak buku, pemahaman ini akan membantu menentukan ukuran dan jumlah papan yang dibutuhkan untuk membuat rak yang kuat dan fungsional.
Pentingnya Memahami Konsep Jaring-Jaring Balok
Memahami konsep jaring-jaring balok merupakan kunci untuk menguasai visualisasi spasial dan pemecahan masalah dalam berbagai konteks. Kemampuan ini tidak hanya penting dalam bidang matematika dan geometri, tetapi juga dalam berbagai disiplin ilmu dan aktivitas sehari-hari, membantu kita dalam merancang, membuat, dan memecahkan masalah yang melibatkan bentuk tiga dimensi.
Variasi Jaring-Jaring Balok
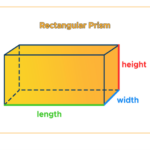
Jaring-jaring balok, meskipun umumnya dikenal dengan bentuk persegi panjang pada alas dan tutupnya, memiliki fleksibilitas bentuk yang lebih luas. Memahami variasi ini penting untuk mengembangkan pemahaman spasial yang lebih komprehensif dan mengeksplorasi kemungkinan desain tiga dimensi yang lebih kreatif.
Kemungkinan Variasi Bentuk Jaring-Jaring Balok
Jaring-jaring balok tidak terbatas pada alas dan tutup berbentuk persegi atau persegi panjang. Bentuk-bentuk bangun datar lainnya, seperti segitiga, trapesium, bahkan bentuk-bentuk tidak beraturan, dapat digunakan sebagai alas dan tutup, selama sisi-sisi tegaknya dapat dihubungkan dengan tepat untuk membentuk balok.
Contoh Jaring-Jaring Balok Tidak Konvensional
Bayangkan sebuah balok dengan alas berbentuk segitiga sama sisi dan tutup yang identik. Jaring-jaringnya akan terdiri dari dua segitiga sama sisi sebagai alas dan tutup, serta tiga persegi panjang yang menghubungkan ketiga sisi segitiga. Atau, pertimbangkan balok dengan alas berbentuk trapesium sama kaki. Jaring-jaringnya akan menampilkan dua trapesium sama kaki sebagai alas dan tutup, dan empat persegi panjang yang menghubungkannya.
Bentuk-bentuk tidak beraturan juga memungkinkan, asalkan dipenuhi syarat geometri untuk membentuk balok yang utuh.
Ilustrasi Jaring-Jaring Balok dengan Alas dan Tutup Berbentuk Segitiga
Untuk balok dengan alas dan tutup berbentuk segitiga sama sisi, bayangkan tiga persegi panjang yang tersusun berdampingan, masing-masing memiliki panjang sisi yang sama dengan sisi segitiga. Di atas dan di bawah susunan persegi panjang tersebut, letakkan dua segitiga sama sisi yang identik. Dengan cara ini, semua sisi akan terhubung untuk membentuk balok ketika dilipat. Ukuran segitiga dan persegi panjang harus disesuaikan agar semua sisi dapat bertemu dengan tepat.
Perbedaan dan Persamaan Jaring-Jaring Balok Berbagai Bentuk
Perbedaan utama terletak pada bentuk alas dan tutupnya. Meskipun bentuk alas dan tutup bervariasi, persamaannya adalah jaring-jaring tersebut selalu terdiri dari enam sisi yang membentuk balok ketika dilipat. Jumlah sisi selalu sama, tetapi bentuk dan ukuran setiap sisi akan berbeda bergantung pada bentuk alas dan tutupnya.
Langkah-Langkah Membuat Jaring-Jaring Balok dengan Alas dan Tutup Berbentuk Trapesium
- Tentukan ukuran trapesium yang akan menjadi alas dan tutup balok. Misalnya, panjang sisi sejajar adalah 5 cm dan 7 cm, dan tinggi trapesium adalah 4 cm.
- Hitung panjang sisi tegak balok. Panjang ini akan sama dengan tinggi trapesium (4 cm).
- Gambarkan dua trapesium identik yang akan menjadi alas dan tutup balok.
- Gambarkan empat persegi panjang. Dua persegi panjang memiliki panjang 5 cm (sisi pendek trapesium) dan lebar 4 cm (tinggi trapesium). Dua persegi panjang lainnya memiliki panjang 7 cm (sisi panjang trapesium) dan lebar 4 cm (tinggi trapesium).
- Susun kedua trapesium dan empat persegi panjang sehingga membentuk jaring-jaring balok yang utuh. Pastikan sisi-sisi yang berdampingan memiliki ukuran yang sama agar dapat dilipat dengan sempurna.
Penutupan Akhir
Memahami konsep jaring-jaring balok beserta alas dan tutupnya memberikan pemahaman yang lebih mendalam tentang geometri ruang dan aplikasinya dalam kehidupan nyata. Kemampuan untuk memvisualisasikan dan menghitung luas permukaan serta volume balok sangat berguna dalam berbagai bidang, mulai dari desain produk hingga arsitektur. Dengan pemahaman yang baik tentang berbagai variasi jaring-jaring balok, kita dapat memecahkan masalah praktis dengan lebih efektif dan kreatif.