Kalkulator akar, alat yang memungkinkan kita menghitung akar kuadrat, kubik, dan bahkan akar pangkat yang lebih tinggi, memiliki sejarah panjang dan menarik. Perjalanan perkembangannya, dari metode manual kuno hingga algoritma canggih di perangkat digital modern, mencerminkan kemajuan luar biasa dalam matematika dan teknologi komputasi. Dari metode Babilonia hingga algoritma Newton-Raphson, kita akan menjelajahi berbagai teknik perhitungan akar dan penerapannya dalam berbagai disiplin ilmu.
Artikel ini akan mengupas tuntas sejarah perkembangan kalkulator akar, menjelaskan algoritma yang mendasarinya, serta membahas penerapannya yang luas dalam berbagai bidang, mulai dari teknik sipil hingga keuangan. Kita juga akan membahas jenis-jenis kalkulator akar yang tersedia, fitur-fiturnya, serta keterbatasan dan potensi kesalahan dalam penggunaannya. Semoga uraian ini memberikan pemahaman komprehensif tentang kalkulator akar dan perannya dalam dunia modern.
Sejarah Perkembangan Kalkulator Akar

Perhitungan akar, khususnya akar kuadrat, telah menjadi bagian penting dari matematika sejak zaman kuno. Perkembangan metode perhitungannya mencerminkan kemajuan teknologi dan pemahaman manusia tentang matematika itu sendiri, dari metode manual yang rumit hingga algoritma canggih yang dijalankan oleh komputer modern.
Metode Perhitungan Akar Kuadrat Sepanjang Sejarah
Metode perhitungan akar kuadrat telah berevolusi secara signifikan selama berabad-abad. Dari metode manual yang membutuhkan ketelitian tinggi dan waktu yang lama, perkembangan teknologi telah menghasilkan metode yang jauh lebih cepat dan akurat.
Kalkulator akar, alat praktis untuk menghitung akar kuadrat, kubik, dan bahkan akar pangkat lebih tinggi, sangat membantu dalam berbagai perhitungan. Bayangkan saja, kegunaannya meluas hingga ke bidang pengobatan tradisional, misalnya dalam menghitung dosis ramuan yang menggunakan akar alang-alang sebagai bahan utamanya. Meskipun rumus dan perhitungannya kompleks, kalkulator akar menyederhanakan prosesnya secara signifikan, memungkinkan kita untuk fokus pada interpretasi hasil daripada proses perhitungan itu sendiri.
Dengan demikian, kalkulator akar menjadi alat yang tak ternilai bagi siapa saja yang membutuhkan akurasi dan efisiensi dalam perhitungan akar.
| Era | Metode | Kecepatan | Akurasi |
|---|---|---|---|
| Zaman Babilonia (sekitar 2000 SM) | Metode iteratif, pendekatan numerik | Relatif lambat, membutuhkan banyak iterasi | Tergantung jumlah iterasi, bisa cukup akurat |
| Yunani Kuno (sekitar 300 SM) | Metode Heron (atau metode Babilonia yang disempurnakan) | Lebih cepat daripada metode Babilonia sederhana | Lebih akurat dengan lebih banyak iterasi |
| Abacus (berbagai era) | Manipulasi manik-manik untuk pendekatan numerik | Tergantung keahlian pengguna, relatif lambat | Tergantung keahlian pengguna, bisa cukup akurat |
| Era Komputer Digital (abad ke-20 hingga sekarang) | Algoritma Newton-Raphson dan metode lainnya | Sangat cepat, hasil instan | Sangat akurat, hingga banyak digit desimal |
Tokoh-Tokoh Penting dalam Pengembangan Metode Perhitungan Akar
Beberapa tokoh penting telah berkontribusi dalam pengembangan metode perhitungan akar. Kontribusi mereka meliputi penyempurnaan metode yang sudah ada dan pengembangan algoritma baru yang lebih efisien.
- Heron dari Alexandria: Dikenal karena metode iteratifnya untuk menghitung akar kuadrat, yang masih digunakan sebagai dasar beberapa algoritma modern.
- Isaac Newton: Metode Newton-Raphson, yang merupakan algoritma iteratif yang sangat efisien untuk mencari akar persamaan, termasuk akar kuadrat.
- Para ilmuwan komputer abad ke-20: Berperan dalam pengembangan algoritma dan implementasinya dalam kalkulator dan komputer digital.
Evolusi Algoritma dalam Kalkulator Akar
Algoritma yang digunakan dalam kalkulator akar telah berkembang dari metode sederhana menjadi algoritma yang kompleks dan efisien. Perkembangan ini didorong oleh peningkatan daya komputasi dan kebutuhan akan kecepatan dan akurasi yang lebih tinggi.
- Metode iteratif sederhana, seperti metode Babilonia, merupakan dasar dari algoritma awal.
- Metode Newton-Raphson dan variasinya menjadi algoritma yang paling umum digunakan karena kecepatan dan akurasinya yang tinggi.
- Algoritma modern juga memanfaatkan teknik-teknik optimasi untuk meminimalkan waktu komputasi dan meningkatkan akurasi.
Perbandingan Kecepatan dan Akurasi Metode Perhitungan Akar
Perbandingan kecepatan dan akurasi metode perhitungan akar di masa lalu dengan metode modern sangat signifikan. Metode modern menawarkan kecepatan dan akurasi yang jauh lebih tinggi.
- Metode manual membutuhkan waktu yang lama dan rentan terhadap kesalahan manusia, sedangkan metode modern memberikan hasil yang hampir instan dan sangat akurat.
- Perbedaan ini disebabkan oleh peningkatan daya komputasi dan pengembangan algoritma yang lebih efisien.
- Sebagai contoh, menghitung akar kuadrat dari angka besar dengan metode manual bisa memakan waktu berjam-jam, sedangkan kalkulator modern dapat melakukannya dalam hitungan detik dengan akurasi hingga beberapa digit desimal.
Algoritma Perhitungan Akar
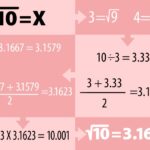
Menghitung akar suatu bilangan, baik akar kuadrat, akar pangkat tiga, atau akar pangkat berapapun, melibatkan penggunaan algoritma tertentu. Berbagai metode telah dikembangkan, masing-masing dengan kelebihan dan kekurangannya sendiri, terutama dalam hal efisiensi dan kompleksitas komputasi. Berikut ini akan dijelaskan beberapa algoritma populer untuk menghitung akar, beserta perbandingan dan ilustrasi penggunaannya.
Metode Newton-Raphson
Metode Newton-Raphson merupakan metode iteratif yang efektif untuk mencari akar dari suatu fungsi. Dalam konteks perhitungan akar, metode ini mendekati akar dengan secara bertahap memperbaiki tebakan awal. Keunggulannya terletak pada kecepatan konvergensi yang tinggi, artinya ia mendekati solusi yang tepat dengan cepat.
Ilustrasi langkah-langkah metode Newton-Raphson dalam menghitung akar kuadrat dari suatu bilangan x:
- Mulailah dengan tebakan awal (x0) untuk akar kuadrat dari x. Tebakan awal ini dapat berupa nilai apapun, tetapi semakin mendekati nilai akar sebenarnya, semakin cepat proses konvergensi.
- Hitung nilai berikutnya ( xn+1) menggunakan rumus iterasi: xn+1 = 0.5
(xn + x / x n)
- Ulangi langkah 2 hingga perbedaan antara xn+1 dan xn mencapai tingkat akurasi yang diinginkan (misalnya, kurang dari 0.0001).
Sebagai contoh, jika kita ingin menghitung akar kuadrat dari 9, kita bisa memulai dengan tebakan awal x0 = 3 . Iterasi pertama akan menghasilkan x1 = 0.5
– (3 + 9/3) = 3 . Karena sudah sama, maka proses konvergensi cepat selesai. Jika kita memulai dengan tebakan x0 = 1 , maka iterasi pertama akan menghasilkan x1 = 5 , iterasi kedua akan menghasilkan x2 = 3.4 , dan seterusnya sampai mendekati 3.
Metode Babilonia
Metode Babilonia, juga dikenal sebagai metode Heron, merupakan metode iteratif yang lebih sederhana dibandingkan Newton-Raphson. Metode ini juga dikenal sejak zaman kuno dan memiliki prinsip yang mirip dengan Newton-Raphson, namun dengan rumus iterasi yang sedikit berbeda. Walaupun lebih sederhana, metode ini tetap efektif untuk menghitung akar kuadrat.
Pseudocode untuk metode Babilonia:
function akarKuadratBabilonia(x, toleransi): tebakanAwal = x / 2 ulang = true sementara ulang: tebakanBaru = 0.5
(tebakanAwal + x / tebakanAwal)
jika |tebakanBaru - tebakanAwal| < toleransi: ulang = false lain: tebakanAwal = tebakanBaru kembalikan tebakanBaru
Perbandingan Kompleksitas Komputasi
Metode Newton-Raphson umumnya memiliki kompleksitas komputasi yang lebih rendah dibandingkan beberapa metode lainnya karena konvergensi kuadratiknya. Ini berarti jumlah iterasi yang dibutuhkan untuk mencapai akurasi tertentu relatif lebih sedikit. Metode Babilonia, meskipun lebih sederhana, memiliki konvergensi yang lebih lambat. Namun, untuk perhitungan sederhana, perbedaan waktu komputasi mungkin tidak signifikan.
Perhitungan Akar Pangkat Tiga dari 27
Kita akan menggunakan metode Newton-Raphson untuk menghitung akar pangkat tiga dari
27. Rumus iterasi untuk akar pangkat tiga adalah: xn+1 = (2
- x n + a / x n2) / 3 , dimana a adalah bilangan yang akar pangkat tiganya dicari. Dengan tebakan awal x0 = 3 , iterasi pertama akan menghasilkan x1 = (2
- 3 + 27 / 3 2) / 3 = 3 .
Karena sudah sama, proses konvergensi cepat selesai dan hasilnya adalah 3.
Penerapan Kalkulator Akar dalam Berbagai Bidang
Kalkulator akar, meskipun tampak sederhana, memiliki peran yang sangat penting dan luas dalam berbagai disiplin ilmu dan aktivitas sehari-hari. Kemampuannya untuk menghitung akar kuadrat, akar pangkat tiga, dan akar pangkat lainnya menjadikannya alat yang tak tergantikan dalam menyelesaikan berbagai permasalahan yang melibatkan besaran kuadrat atau berpangkat.
Penerapan kalkulator akar ini merambah berbagai bidang, dari perhitungan struktur bangunan hingga analisis data keuangan. Ketepatan dan efisiensi yang ditawarkan kalkulator akar secara signifikan meningkatkan kecepatan dan akurasi dalam berbagai proses perhitungan.
Penerapan Kalkulator Akar dalam Teknik Sipil
Dalam teknik sipil, khususnya dalam perhitungan struktur bangunan, kalkulator akar berperan krusial. Misalnya, dalam menentukan panjang diagonal suatu bangunan persegi atau menghitung gaya tekan dan tarik pada struktur bangunan, kalkulator akar digunakan untuk menyelesaikan persamaan matematika yang melibatkan teorema Pythagoras. Ketepatan perhitungan akar sangat penting untuk memastikan stabilitas dan keamanan struktur bangunan.
Penerapan Kalkulator Akar dalam Fisika
Di bidang fisika, kalkulator akar sering digunakan dalam berbagai perhitungan, termasuk perhitungan kecepatan dan percepatan. Misalnya, dalam menentukan kecepatan akhir suatu objek yang jatuh bebas, rumus yang digunakan melibatkan akar kuadrat dari percepatan gravitasi dan jarak jatuh. Selain itu, kalkulator akar juga digunakan dalam perhitungan energi kinetik dan momentum.
Sebagai contoh, jika sebuah benda jatuh dari ketinggian 10 meter dengan percepatan gravitasi 9.8 m/s², kecepatan benda saat menyentuh tanah dapat dihitung menggunakan rumus v = √(2gh), dimana v adalah kecepatan, g adalah percepatan gravitasi, dan h adalah ketinggian. Kalkulator akar akan sangat membantu dalam menghitung nilai v dengan cepat dan akurat.
Penerapan Kalkulator Akar dalam Keuangan
Dalam bidang keuangan, kalkulator akar digunakan dalam berbagai perhitungan, seperti perhitungan nilai investasi dan pengembalian investasi. Misalnya, dalam menghitung standar deviasi dari portofolio investasi, kalkulator akar digunakan untuk menghitung akar kuadrat dari varians. Standar deviasi ini merupakan ukuran risiko investasi.
Sebagai contoh, dalam menghitung tingkat pengembalian tahunan suatu investasi, jika diketahui nilai investasi awal, nilai investasi akhir, dan jumlah tahun investasi, kalkulator akar dapat digunakan untuk menentukan tingkat pertumbuhan tahunan rata-rata (Compound Annual Growth Rate atau CAGR).
Peran Kalkulator Akar dalam Pengembangan Ilmu Pengetahuan dan Teknologi
Kalkulator akar berperan penting dalam pengembangan ilmu pengetahuan dan teknologi karena kemampuannya untuk mempercepat dan menyederhanakan perhitungan kompleks. Kemajuan dalam teknologi kalkulator akar memungkinkan para ilmuwan dan teknisi untuk menyelesaikan masalah yang sebelumnya membutuhkan waktu dan usaha yang sangat besar. Hal ini telah berkontribusi pada kemajuan di berbagai bidang, termasuk kedokteran, teknik, dan ilmu komputer.
Bidang Lain yang Memanfaatkan Kalkulator Akar
- Survei dan Pemetaan: Menghitung jarak dan koordinat.
- Astronomi: Menghitung jarak antar benda langit.
- Statistika: Menghitung standar deviasi dan varians.
- Kedokteran: Analisis data medis dan perhitungan dosis obat.
- Arsitektur: Perhitungan dimensi dan proporsi bangunan.
Jenis-jenis Kalkulator Akar dan Fitur-fiturnya
Kalkulator akar, alat sederhana namun ampuh, hadir dalam berbagai bentuk dan kemampuan, mulai dari perangkat sederhana untuk menghitung akar kuadrat hingga kalkulator ilmiah canggih yang mampu menangani berbagai operasi matematika yang kompleks. Pemahaman tentang jenis-jenis kalkulator akar dan fitur-fiturnya akan membantu Anda memilih alat yang paling sesuai dengan kebutuhan perhitungan Anda.
Jenis-jenis Kalkulator Akar
Kalkulator akar dapat dikategorikan berdasarkan kemampuan dan kompleksitasnya. Secara umum, kita dapat membedakan kalkulator akar sederhana, kalkulator ilmiah, dan kalkulator khusus.
- Kalkulator Sederhana: Biasanya hanya memiliki fungsi dasar seperti penjumlahan, pengurangan, perkalian, pembagian, dan penghitungan akar kuadrat. Desainnya ringkas dan mudah digunakan, cocok untuk perhitungan sehari-hari.
- Kalkulator Ilmiah: Menawarkan berbagai fungsi matematika tingkat lanjut, termasuk trigonometri, logaritma, eksponensial, dan berbagai jenis akar (akar pangkat tiga, akar pangkat empat, dan seterusnya). Kalkulator ilmiah seringkali memiliki tampilan yang lebih besar dan tombol yang lebih banyak.
- Kalkulator Khusus: Dikembangkan untuk tujuan spesifik, misalnya kalkulator untuk keperluan teknik, keuangan, atau statistika. Kalkulator ini seringkali memiliki fungsi-fungsi yang disesuaikan dengan bidang keahliannya.
Perbandingan Fitur Kalkulator Akar
Tabel berikut membandingkan fitur-fitur umum dari berbagai jenis kalkulator akar:
| Jenis Kalkulator | Fungsi Akar | Fungsi Lainnya | Ukuran dan Portabilitas |
|---|---|---|---|
| Kalkulator Sederhana | Akar Kuadrat | Penjumlahan, Pengurangan, Perkalian, Pembagian | Kecil dan Ringan |
| Kalkulator Ilmiah | Akar Kuadrat, Akar Kubik, dan lainnya | Trigonometri, Logaritma, Eksponensial, Statistik | Sedang, relatif mudah dibawa |
| Kalkulator Khusus (Contoh: Keuangan) | Akar Kuadrat (mungkin lebih banyak tergantung spesifikasi) | Fungsi keuangan (misalnya, nilai sekarang, nilai masa depan) | Bervariasi, tergantung desain |
Perbedaan Kalkulator Akar Berbasis Software dan Hardware
Kalkulator akar dapat berupa perangkat keras (hardware) atau perangkat lunak (software). Kalkulator hardware adalah perangkat fisik yang dapat dipegang dan dioperasikan secara langsung. Sementara itu, kalkulator software adalah program komputer yang berjalan pada perangkat seperti komputer, tablet, atau smartphone.
Kalkulator hardware umumnya lebih portabel dan tidak membutuhkan koneksi internet, sedangkan kalkulator software menawarkan fleksibilitas yang lebih tinggi dan akses ke fitur-fitur yang lebih canggih. Kalkulator software juga seringkali menawarkan tampilan grafis yang lebih baik.
Fitur Canggih Kalkulator Akar Modern
Kalkulator akar modern, khususnya yang berbasis software, seringkali dilengkapi dengan fitur-fitur canggih seperti:
- Penyimpanan Riwayat Perhitungan: Memudahkan pengguna untuk meninjau perhitungan sebelumnya.
- Fungsi Grafik: Memvisualisasikan fungsi matematika, termasuk fungsi akar.
- Konversi Satuan: Memudahkan konversi antara berbagai satuan.
- Integrasi dengan Aplikasi Lain: Memungkinkan pengguna untuk berbagi hasil perhitungan dengan aplikasi lain.
Kelebihan dan Kekurangan Kalkulator Akar Online
Kelebihan kalkulator akar online antara lain kemudahan akses, ketersediaan berbagai fitur, dan seringkali gratis. Namun, kekurangannya termasuk ketergantungan pada koneksi internet dan potensi masalah keamanan data jika tidak menggunakan situs yang terpercaya.
Keterbatasan dan Kesalahan Kalkulator Akar
Kalkulator akar, baik digital maupun manual, memiliki keterbatasan dalam hal akurasi perhitungan. Meskipun memberikan hasil yang cepat dan praktis, penting untuk memahami potensi kesalahan yang mungkin terjadi dan bagaimana meminimalisirnya. Pemahaman ini akan membantu kita dalam menginterpretasi hasil perhitungan dan menghindari kesimpulan yang salah.
Kesalahan Pembulatan dalam Perhitungan Akar
Kesalahan pembulatan merupakan salah satu sumber kesalahan umum dalam perhitungan akar. Kalkulator digital bekerja dengan jumlah digit terbatas, sehingga angka desimal sering dibulatkan untuk menyesuaikan kapasitas memori. Proses pembulatan ini dapat menyebabkan penyimpangan kecil, namun jika akumulasi kesalahan ini terjadi dalam perhitungan yang lebih kompleks, hasilnya bisa menjadi tidak akurat. Besarnya kesalahan pembulatan bergantung pada jumlah digit signifikan yang ditampilkan oleh kalkulator dan algoritma pembulatan yang digunakan.
Keterbatasan Akurasi Kalkulator Akar Digital
Akurasi kalkulator akar digital dipengaruhi oleh beberapa faktor, termasuk algoritma perhitungan yang digunakan, kapasitas memori, dan representasi bilangan internal. Algoritma yang kurang efisien dapat menghasilkan kesalahan yang lebih besar. Kapasitas memori yang terbatas membatasi jumlah digit yang dapat ditampilkan, sehingga angka dibulatkan. Representasi bilangan internal (misalnya, floating-point) juga dapat menyebabkan kesalahan karena ketidakmampuan untuk merepresentasikan semua bilangan real dengan tepat.
Contoh Kasus Perhitungan Akar yang Menghasilkan Kesalahan
Misalnya, perhitungan akar kuadrat dari 2 menggunakan kalkulator yang hanya menampilkan 8 digit desimal. Hasilnya mungkin 1.41421356. Namun, nilai sebenarnya dari akar kuadrat 2 memiliki jumlah desimal yang tak terhingga. Perbedaan antara hasil kalkulator dan nilai sebenarnya merupakan kesalahan pembulatan. Semakin banyak digit desimal yang ditampilkan, semakin kecil kesalahan pembulatannya.
Perbedaan ini mungkin tampak kecil, namun dapat signifikan dalam perhitungan yang lebih kompleks.
Saran untuk Meminimalisir Kesalahan dalam Penggunaan Kalkulator Akar
- Gunakan kalkulator dengan presisi tinggi, yang mampu menampilkan lebih banyak digit desimal.
- Periksa kembali hasil perhitungan dengan metode alternatif, misalnya dengan menggunakan kalkulator lain atau metode perhitungan manual.
- Sadari batasan akurasi kalkulator dan jangan mengandalkan hasil perhitungan sebagai kebenaran mutlak. Pertimbangkan margin of error yang mungkin terjadi.
- Jika memungkinkan, gunakan software matematika yang lebih canggih yang memiliki kemampuan untuk menghitung dengan presisi lebih tinggi.
Akhir Kata: Kalkulator Akar
Perjalanan panjang kalkulator akar, dari metode manual hingga teknologi digital modern, menunjukkan bagaimana inovasi terus mendorong peningkatan akurasi dan efisiensi dalam perhitungan matematika. Memahami algoritma yang mendasari kalkulator akar tidak hanya penting bagi para ilmuwan dan insinyur, tetapi juga memberikan apresiasi yang lebih dalam terhadap kekuatan dan keterbatasan teknologi komputasi. Dengan pemahaman yang lebih baik tentang potensi kesalahan dan cara mengatasinya, kita dapat memanfaatkan kalkulator akar dengan lebih efektif dan akurat dalam berbagai aplikasi.