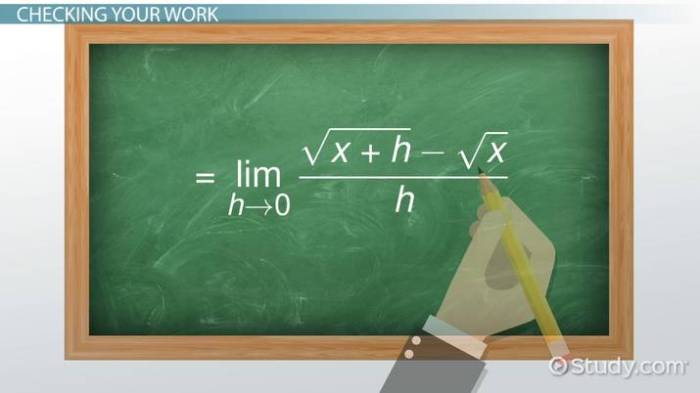
Limit tak hingga akar merupakan konsep penting dalam kalkulus yang membahas perilaku fungsi ketika variabel mendekati tak hingga, khususnya ketika fungsi tersebut melibatkan operasi akar. Memahami konsep ini memungkinkan kita untuk menganalisis perilaku fungsi yang kompleks dan menyelesaikan masalah dalam berbagai bidang, mulai dari fisika hingga ekonomi. Konsep limit tak hingga akar pada dasarnya mengkaji bagaimana nilai fungsi mendekati suatu nilai tertentu atau menuju tak hingga ketika variabel bebasnya semakin besar atau kecil tanpa batas.
Penggunaan teknik-teknik tertentu, seperti manipulasi aljabar dan aturan L’Hôpital, sangat krusial dalam menentukan nilai limit ini.
Artikel ini akan membahas secara detail bagaimana menentukan limit tak hingga yang melibatkan akar, baik itu akar kuadrat, akar pangkat tiga, maupun kombinasi dengan fungsi rasional lainnya. Kita akan mempelajari langkah-langkah penyelesaian, contoh soal yang beragam, serta penerapan konsep ini dalam konteks dunia nyata. Dengan pemahaman yang mendalam tentang limit tak hingga akar, Anda akan mampu menyelesaikan masalah yang lebih kompleks dan mengaplikasikannya dalam berbagai disiplin ilmu.
Limit Tak Hingga dan Konsepnya

Limit tak hingga merupakan konsep penting dalam kalkulus yang menjelaskan perilaku suatu fungsi ketika variabel bebas mendekati suatu nilai tertentu, baik itu nilai hingga maupun tak hingga, dan nilai fungsi tersebut mendekati tak hingga. Konsep ini membantu kita memahami bagaimana fungsi berperilaku pada batas-batas tertentu, khususnya ketika nilai fungsi “meledak” menuju tak hingga positif atau negatif.
Konsep limit tak hingga berbeda dengan limit biasa yang menghasilkan nilai hingga. Pada limit biasa, kita mencari nilai yang didekati fungsi saat variabel mendekati suatu nilai tertentu. Sementara pada limit tak hingga, kita mengamati bagaimana fungsi tersebut “bertumbuh” tanpa batas, mendekati tak hingga positif atau negatif.
Contoh Fungsi dengan Limit Tak Hingga
Perhatikan fungsi f(x) = 1/x. Ketika x mendekati 0 dari arah kanan (x → 0+), nilai f(x) mendekati tak hingga positif (∞). Sebaliknya, ketika x mendekati 0 dari arah kiri (x → 0-), nilai f(x) mendekati tak hingga negatif (-∞). Ini merupakan contoh limit tak hingga dimana nilai fungsi mendekati tak hingga saat variabel mendekati nilai tertentu.
Contoh lain adalah fungsi f(x) = x². Ketika x mendekati tak hingga (x → ∞), nilai f(x) juga mendekati tak hingga positif (∞). Fungsi ini menunjukkan limit tak hingga ketika variabel bebas mendekati tak hingga.
Ilustrasi Grafik Fungsi dengan Limit Tak Hingga
Bayangkan grafik fungsi f(x) = 1/x. Grafik ini memiliki asimtot vertikal pada x = 0. Ketika x mendekati 0 dari arah kanan (nilai x positif dan mendekati 0), nilai y (f(x)) akan terus meningkat tanpa batas, mendekati tak hingga positif. Grafik akan mendekati sumbu y positif tetapi tidak akan pernah menyentuhnya. Sebaliknya, ketika x mendekati 0 dari arah kiri (nilai x negatif dan mendekati 0), nilai y akan terus menurun tanpa batas, mendekati tak hingga negatif.
Grafik akan mendekati sumbu y negatif tetapi tidak akan pernah menyentuhnya. Grafik ini dengan jelas menunjukkan konsep limit tak hingga dimana fungsi mendekati tak hingga saat x mendekati 0.
Perbandingan Limit Tak Hingga dan Limit Biasa
Tabel berikut membandingkan limit tak hingga dengan limit biasa:
| Jenis Limit | Definisi | Contoh Fungsi | Hasil Limit |
|---|---|---|---|
| Limit Biasa | Nilai yang didekati fungsi saat variabel mendekati nilai tertentu. | limx→2 (x²
|
4 |
| Limit Tak Hingga Positif | Nilai fungsi mendekati tak hingga positif saat variabel mendekati nilai tertentu atau tak hingga. | limx→0+ 1/x | ∞ |
| Limit Tak Hingga Negatif | Nilai fungsi mendekati tak hingga negatif saat variabel mendekati nilai tertentu atau tak hingga. | limx→0- 1/x | -∞ |
| Limit Tak Hingga (x→∞) | Nilai fungsi mendekati tak hingga saat variabel mendekati tak hingga. | limx→∞ x² | ∞ |
Menentukan Limit Tak Hingga Fungsi Rasional: Limit Tak Hingga Akar

Menentukan limit tak hingga dari fungsi rasional merupakan konsep penting dalam kalkulus. Memahami bagaimana limit ini dihitung akan membantu kita menganalisis perilaku fungsi pada nilai x yang sangat besar atau sangat kecil.
Secara umum, limit tak hingga fungsi rasional bergantung pada derajat pembilang dan penyebut fungsi tersebut. Berikut akan dijelaskan langkah-langkah dan contohnya.
Prosedur Menentukan Limit Tak Hingga Fungsi Rasional
Untuk menentukan limit tak hingga dari fungsi rasional, kita dapat mengikuti langkah-langkah berikut:
- Tentukan derajat pembilang (n) dan derajat penyebut (m) fungsi rasional.
- Bandingkan derajat pembilang dan penyebut:
- Jika n < m, limitnya adalah 0.
- Jika n = m, limitnya adalah rasio koefisien suku berderajat tertinggi pembilang dan penyebut.
- Jika n > m, limitnya adalah ∞ atau -∞, tergantung pada koefisien suku berderajat tertinggi dan tanda x.
Contoh Soal: Derajat Pembilang Lebih Tinggi dari Penyebut
Misalkan kita memiliki fungsi rasional f(x) = (3x² + 2x)/(x – 1). Kita ingin mencari lim x→∞ f(x).
Karena derajat pembilang (2) lebih tinggi daripada derajat penyebut (1), limitnya akan menuju tak hingga. Untuk menentukan apakah menuju ∞ atau -∞, kita perhatikan koefisien suku berderajat tertinggi. Pada pembilang, koefisien x² adalah 3 (positif), dan pada penyebut, koefisien x adalah 1 (positif). Karena keduanya positif, limitnya akan menuju ∞.
Secara formal: lim x→∞ (3x² + 2x)/(x – 1) = ∞
Contoh Soal: Derajat Pembilang Lebih Rendah dari Penyebut
Misalkan fungsi rasionalnya adalah g(x) = (x + 1)/(2x²
-3). Kita ingin mencari lim x→∞ g(x).
Karena derajat pembilang (1) lebih rendah daripada derajat penyebut (2), limitnya adalah 0.
Secara formal: lim x→∞ (x + 1)/(2x²
-3) = 0
Contoh Soal: Derajat Pembilang Sama dengan Penyebut
Misalkan fungsi rasionalnya adalah h(x) = (4x + 5)/(2x – 1). Kita ingin mencari lim x→∞ h(x).
Karena derajat pembilang dan penyebut sama-sama 1, limitnya adalah rasio koefisien suku berderajat tertinggi. Rasio koefisien suku berderajat tertinggi adalah 4/2 = 2.
Secara formal: lim x→∞ (4x + 5)/(2x – 1) = 2
Asimtot Horizontal dan Limit Tak Hingga Fungsi Rasional
Asimtot horizontal dari sebuah fungsi rasional menggambarkan perilaku fungsi ketika x mendekati tak hingga (positif atau negatif). Limit tak hingga fungsi rasional berhubungan langsung dengan asimtot horizontal. Jika limit tak hingga mendekati suatu nilai konstan ‘c’, maka garis y = c merupakan asimtot horizontal dari fungsi tersebut. Jika limitnya menuju tak hingga, maka tidak terdapat asimtot horizontal.
Limit Tak Hingga Fungsi Trigonometri

Limit tak hingga pada fungsi trigonometri merupakan topik menarik dalam kalkulus. Memahami perilaku fungsi-fungsi seperti sinus, kosinus, dan tangen saat variabel mendekati tak hingga akan membantu kita menyelesaikan berbagai masalah matematika dan fisika. Pada bagian ini, kita akan menjelajahi limit tak hingga dari fungsi trigonometri dasar dan penerapan aturan L’Hôpital dalam konteks ini.
Limit Tak Hingga Fungsi Trigonometri Dasar
Fungsi trigonometri dasar, yaitu sin x, cos x, dan tan x, memiliki perilaku yang unik ketika x mendekati tak hingga. Perhatikan bahwa nilai sin x dan cos x akan selalu berada di antara -1 dan 1, berosilasi secara periodik tanpa mendekati nilai tertentu. Sedangkan tan x akan terus berosilasi antara tak hingga positif dan tak hingga negatif.
Oleh karena itu, limit tak hingga dari sin x dan cos x tidak ada, sedangkan limit tak hingga dari tan x juga tidak ada.
Contoh Soal dan Penyelesaian Limit Tak Hingga yang Melibatkan Fungsi Trigonometri dan Fungsi Aljabar, Limit tak hingga akar
Mari kita perhatikan contoh berikut. Misalkan kita ingin mencari limit dari limx→∞ (sin x) / x
. Karena -1 ≤ sin x ≤ 1 untuk semua x, maka kita dapat menggunakan teorema apit (sandwich theorem). Kita tahu bahwa -1/x ≤ (sin x)/x ≤ 1/x
. Ketika x mendekati tak hingga, baik -1/x maupun 1/x mendekati 0.
Oleh karena itu, berdasarkan teorema apit, limit dari (sin x)/x ketika x mendekati tak hingga adalah 0.
Penerapan Aturan L’Hôpital pada Limit Tak Hingga Fungsi Trigonometri
Aturan L’Hôpital sangat berguna dalam menyelesaikan limit tak hingga yang berbentuk tak tentu, seperti 0/0 atau ∞/∞. Perhatikan contoh berikut: limx→∞ (x sin(1/x))
. Jika kita langsung substitusikan x dengan ∞, kita akan mendapatkan bentuk tak tentu ∞
– 0. Kita dapat menulis ulang ekspresi tersebut sebagai limx→∞ sin(1/x) / (1/x)
. Sekarang bentuknya menjadi 0/0, sehingga kita dapat menerapkan aturan L’Hôpital.
Turunan dari pembilang adalah cos(1/x)
– (-1/x²) dan turunan dari penyebut adalah -1/x². Setelah penyederhanaan, kita mendapatkan limx→∞ cos(1/x)
= cos(0) = 1.
Contoh Soal Menantang Limit Tak Hingga Fungsi Trigonometri
Carilah nilai dari limx→∞ (x² sin(1/x) + cos x) / (x² + 1)
.
Penyelesaian:
- Kita dapat membagi pembilang dan penyebut dengan x²:
- Ekspresi menjadi
limx→∞ (sin(1/x) / 1 + cos x/x²) / (1 + 1/x²)
. - Saat x mendekati ∞, 1/x mendekati 0, dan cos x/x² mendekati 0, dan 1/x² mendekati 0.
- Oleh karena itu, limitnya menjadi (sin 0 + 0) / (1 + 0) = 0/1 = 0.
Limit Tak Hingga dan Akar
Menentukan limit tak hingga yang melibatkan akar membutuhkan pemahaman yang baik tentang sifat-sifat limit dan manipulasi aljabar. Seringkali, kita perlu menggunakan teknik-teknik khusus untuk menyederhanakan ekspresi sebelum dapat mengevaluasi limitnya. Berikut ini akan dijelaskan beberapa contoh dan teknik yang umum digunakan.
Limit Tak Hingga dengan Akar Kuadrat
Menentukan limit tak hingga fungsi yang mengandung akar kuadrat seringkali melibatkan pembagian dengan pangkat tertinggi x di dalam akar. Hal ini bertujuan untuk menyederhanakan ekspresi dan memudahkan evaluasi limit.
Contoh: Tentukan
Penyelesaian: Kita dapat mengalikan dengan bentuk konjugatnya:
Selanjutnya, bagi pembilang dan penyebut dengan x:
Jadi, limitnya adalah 1.
Limit Tak Hingga dengan Akar Pangkat Tiga
Prinsip penyelesaian limit tak hingga yang melibatkan akar pangkat tiga serupa dengan akar kuadrat, yaitu dengan menyederhanakan ekspresi melalui manipulasi aljabar dan pembagian dengan pangkat tertinggi x.
Contoh: Tentukan
Penyelesaian: Kita dapat membagi pembilang dan penyebut dengan x:
Jadi, limitnya adalah 1.
Limit Tak Hingga dengan Akar dan Fungsi Rasional
Limit tak hingga yang melibatkan akar dan fungsi rasional seringkali dapat diselesaikan dengan cara yang sama seperti contoh sebelumnya, yaitu dengan membagi pembilang dan penyebut dengan pangkat tertinggi x.
Contoh: Tentukan
Penyelesaian: Bagi pembilang dan penyebut dengan x 2:
Jadi, limitnya adalah 1.
Teknik Khusus untuk Limit Tak Hingga yang Melibatkan Akar
Beberapa teknik khusus yang sering digunakan untuk menyelesaikan limit tak hingga yang melibatkan akar meliputi:
- Mengalikan dengan bentuk konjugat: Teknik ini efektif untuk menyelesaikan limit yang melibatkan selisih atau jumlah akar.
- Membagi dengan pangkat tertinggi x: Teknik ini digunakan untuk menyederhanakan ekspresi dan memudahkan evaluasi limit.
- Menggunakan teorema limit: Teorema limit seperti teorema squeeze atau aturan L’Hôpital dapat digunakan dalam kasus-kasus tertentu.
- Manipulasi aljabar: Terkadang, manipulasi aljabar sederhana seperti pemfaktoran atau penyederhanaan pecahan dapat membantu menyelesaikan limit.
Penerapan Limit Tak Hingga
Konsep limit tak hingga, meskipun tampak abstrak, memiliki aplikasi yang luas dan penting dalam berbagai disiplin ilmu. Memahami bagaimana limit tak hingga bekerja memungkinkan kita untuk menganalisis perilaku fungsi ketika variabelnya mendekati tak hingga, memberikan wawasan yang berharga dalam pemodelan dan prediksi berbagai fenomena.
Penerapan Limit Tak Hingga dalam Fisika
Dalam fisika, limit tak hingga sering digunakan untuk mendekati sistem dengan jumlah partikel yang sangat besar atau untuk menggambarkan perilaku sistem pada skala yang sangat kecil atau sangat besar. Contohnya, dalam mekanika statistik, kita dapat menggunakan limit tak hingga untuk menghitung sifat-sifat makroskopik suatu sistem dari sifat-sifat mikroskopiknya. Misalnya, untuk menghitung tekanan gas ideal, kita mempertimbangkan limit jumlah partikel mendekati tak hingga.
Rumus tekanan gas ideal (P = NkT/V) dapat diturunkan dengan menggunakan konsep limit tak hingga, di mana N (jumlah partikel) mendekati tak hingga. Semakin banyak partikel yang dipertimbangkan, semakin akurat pendekatan tekanan gas ideal terhadap tekanan sebenarnya. Perhitungan ini melibatkan analisis perilaku fungsi tekanan terhadap jumlah partikel ketika jumlah partikel mendekati tak hingga.
Penerapan Limit Tak Hingga dalam Ekonomi
Dalam ekonomi, limit tak hingga sering digunakan dalam model pertumbuhan ekonomi jangka panjang. Misalnya, model Solow-Swan menggunakan konsep limit tak hingga untuk menganalisis perilaku ekonomi dalam jangka panjang, ketika modal dan tenaga kerja mendekati tak hingga. Model ini menganalisis bagaimana tingkat pertumbuhan ekonomi akan berubah seiring waktu, mendekati suatu keadaan tetap (steady state) di mana tingkat pertumbuhan ekonomi menjadi konstan.
Analisis ini melibatkan studi perilaku fungsi produksi ketika jumlah modal dan tenaga kerja mendekati tak hingga, memungkinkan prediksi pertumbuhan ekonomi jangka panjang.
Limit Tak Hingga dalam Pemodelan Matematika
Limit tak hingga merupakan alat fundamental dalam berbagai cabang matematika, termasuk kalkulus dan analisis. Ia digunakan untuk mendefinisikan konsep-konsep seperti konvergensi deret tak hingga, integral tak tentu, dan asimtot. Pemodelan matematika seringkali melibatkan penyederhanaan sistem kompleks dengan mengasumsikan beberapa variabel mendekati tak hingga. Misalnya, dalam pemodelan populasi, kita mungkin menggunakan limit tak hingga untuk menganalisis perilaku populasi dalam jangka waktu yang sangat lama.
Tabel Penerapan Limit Tak Hingga
| Bidang | Contoh Penerapan | Penjelasan Singkat | Manfaat |
|---|---|---|---|
| Fisika | Mekanika Statistik (Gas Ideal) | Menghitung tekanan gas dengan jumlah partikel mendekati tak hingga. | Menghasilkan rumus tekanan gas ideal yang akurat. |
| Ekonomi | Model Pertumbuhan Solow-Swan | Menganalisis pertumbuhan ekonomi jangka panjang dengan modal dan tenaga kerja mendekati tak hingga. | Memprediksi pertumbuhan ekonomi jangka panjang dan keadaan tetap. |
| Matematika | Konvergensi Deret Tak Hingga | Menentukan apakah deret tak hingga konvergen atau divergen. | Mempelajari perilaku deret dan menentukan jumlahnya jika konvergen. |
| Statistika | Teori Probabilitas (Hukum Bilangan Besar) | Menunjukkan bahwa rata-rata sampel mendekati rata-rata populasi ketika ukuran sampel mendekati tak hingga. | Memberikan dasar untuk inferensi statistik. |
Skenario Aplikasi Limit Tak Hingga dalam Kehidupan Sehari-hari
Bayangkan sebuah perusahaan yang ingin memprediksi keuntungannya dalam jangka panjang. Dengan asumsi pertumbuhan penjualan yang konstan, perusahaan dapat menggunakan konsep limit tak hingga untuk memproyeksikan keuntungannya ketika waktu mendekati tak hingga. Dalam skenario ini, kita dapat memodelkan keuntungan sebagai fungsi waktu, dan kemudian menganalisis perilaku fungsi tersebut ketika waktu mendekati tak hingga. Hasil analisis ini akan memberikan gambaran mengenai keuntungan perusahaan dalam jangka panjang, membantu dalam pengambilan keputusan strategis.
Ringkasan Akhir
Limit tak hingga akar, meskipun tampak kompleks pada awalnya, merupakan konsep yang elegan dan berdaya guna. Kemampuan untuk menentukan limit ini membuka jalan untuk memahami perilaku fungsi dalam rentang nilai yang sangat luas. Dengan menguasai teknik-teknik yang telah dibahas, Anda tidak hanya mampu menyelesaikan soal-soal kalkulus, tetapi juga mampu menerapkannya dalam berbagai model matematika di berbagai bidang ilmu pengetahuan dan teknologi.
Pengetahuan ini akan menjadi aset berharga dalam perjalanan akademis dan profesional Anda.

