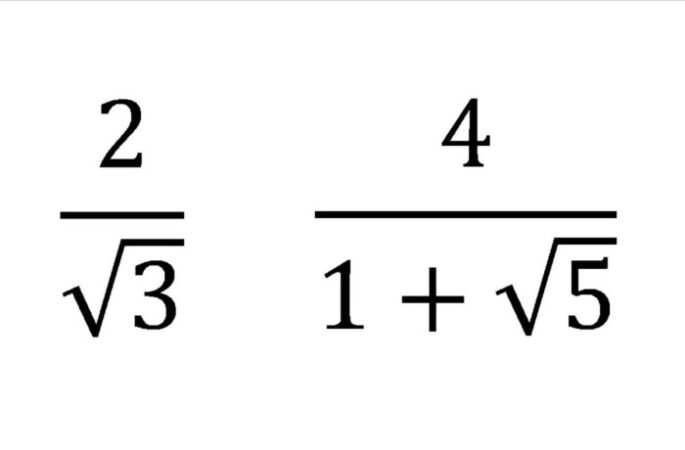Merasionalkan bentuk akar kelas 10 merupakan topik penting dalam aljabar yang mengajarkan cara menyederhanakan bentuk akar agar penyebutnya tidak lagi mengandung akar. Memahami konsep ini akan membuka pintu untuk menyelesaikan berbagai soal matematika, termasuk soal-soal geometri dan fisika yang melibatkan akar. Proses merasionalkan melibatkan teknik-teknik khusus, seperti perkalian dengan sekawan, yang akan dibahas secara detail dalam panduan ini.
Panduan ini akan membahas pengertian merasionalkan bentuk akar, metode-metode yang digunakan, serta penerapannya dalam berbagai konteks. Dari pemahaman dasar hingga soal-soal latihan yang menantang, semua akan dijelaskan secara sistematis dan mudah dipahami. Siap untuk menguasai teknik merasionalkan bentuk akar?
Merasionalkan Bentuk Akar

Merasionalkan bentuk akar merupakan proses menyederhanakan bentuk akar sedemikian rupa sehingga penyebut atau bagian tertentu dari suatu bentuk akar tidak lagi mengandung akar. Proses ini penting dalam matematika untuk menyederhanakan hasil perhitungan dan memudahkan operasi selanjutnya, terutama dalam aljabar dan kalkulus.
Dengan merasionalkan bentuk akar, kita menghilangkan akar dari penyebut pecahan sehingga operasi perhitungan menjadi lebih mudah dan hasilnya lebih rapi. Proses ini melibatkan manipulasi aljabar yang cermat, memanfaatkan sifat-sifat operasi bilangan dan bentuk akar.
Bentuk Akar Rasional dan Irasional
Perbedaan mendasar antara bentuk akar rasional dan irasional terletak pada keberadaan akar dalam penyebut pecahan atau ekspresi aljabar. Bentuk akar rasional tidak memiliki akar pada penyebut, sedangkan bentuk akar irasional memiliki akar pada penyebut.
Perbandingan Bentuk Akar Rasional dan Irasional
| Bentuk Akar | Rasional/Irasional | Penjelasan | Contoh |
|---|---|---|---|
|
Pecahan dengan akar pada penyebut |
Irasional |
Bentuk akar irasional mengandung akar pada penyebut pecahan, sehingga nilai pecahan tersebut merupakan bilangan irasional. |
1/√2, 3/√5, (2+√3)/(1-√2) |
|
Pecahan tanpa akar pada penyebut |
Rasional |
Bentuk akar rasional tidak memiliki akar pada penyebut pecahan, atau jika ada akar, akar tersebut sudah disederhanakan sehingga penyebutnya berupa bilangan rasional. |
√2/2, 3√5/5, (2+√3)(1+√2)/(1-2) |
|
Bilangan bulat atau pecahan tanpa akar |
Rasional |
Bilangan rasional adalah bilangan yang dapat dinyatakan sebagai pecahan a/b, dimana a dan b adalah bilangan bulat dan b ≠ 0. |
2, 3/4, -5 |
|
Akar dari bilangan yang bukan kuadrat sempurna |
Irasional |
Akar dari bilangan yang bukan kuadrat sempurna menghasilkan bilangan irasional. |
√3, √7, √11 |
Jenis-jenis Bentuk Akar dalam Merasionalkan Bentuk Akar
Beberapa jenis bentuk akar umum yang sering dijumpai dalam soal merasionalkan bentuk akar antara lain:
- Pecahan dengan akar pada penyebutnya (misalnya, 1/√2)
- Pecahan dengan bentuk akar binomial pada penyebutnya (misalnya, 1/(√2 + √3))
- Ekspresi aljabar yang mengandung akar pada penyebut atau pembilangnya.
- Ekspresi yang melibatkan operasi penjumlahan, pengurangan, perkalian, atau pembagian bentuk akar.
Merasionalkan Bentuk Akar
Merasionalkan bentuk akar merupakan proses menghilangkan akar pada penyebut suatu pecahan. Proses ini penting dalam matematika karena menyederhanakan bentuk pecahan dan memudahkan perhitungan lebih lanjut. Metode yang paling umum digunakan adalah perkalian dengan sekawan.
Merasionalkan Bentuk Akar dengan Perkalian Sekawan
Perkalian sekawan adalah teknik yang digunakan untuk menghilangkan akar pada penyebut. Sekawan dari a + √b adalah a – √b, dan sebaliknya. Dengan mengalikan pembilang dan penyebut dengan sekawan penyebut, kita dapat memanfaatkan sifat (a + √b)(a – √b) = a²
-b untuk menghilangkan akar pada penyebut.
Contoh: Rasionalkan 2 / (3 + √5)
Penyelesaian: Kalikan pembilang dan penyebut dengan sekawan penyebut, yaitu (3 – √5):
2 / (3 + √5) = [2(3 – √5)] / [(3 + √5)(3 – √5)] = [6 – 2√5] / (9 – 5) = (6 – 2√5) / 4 = (3 – √5) / 2
Merasionalkan Bentuk Akar dengan Penjumlahan atau Pengurangan dalam Penyebut
Jika penyebut mengandung penjumlahan atau pengurangan bentuk akar, proses merasionalkan tetap sama, yaitu dengan mengalikan pembilang dan penyebut dengan sekawan penyebut. Perlu ketelitian dalam mengalikan dan menyederhanakan bentuk aljabar yang dihasilkan.
Contoh: Rasionalkan (√2 + 1) / (√3 – √2)
Penyelesaian: Sekawan dari (√3 – √2) adalah (√3 + √2). Maka:
(√2 + 1) / (√3 – √2) = [(√2 + 1)(√3 + √2)] / [(√3 – √2)(√3 + √2)] = (√6 + 2 + √3 + √2) / (3 – 2) = √6 + 2 + √3 + √2
Merasionalkan Bentuk Akar yang Memuat Akar di Dalam Akar
Merasionalkan bentuk akar yang memuat akar di dalam akar memerlukan beberapa langkah. Langkah pertama biasanya menyederhanakan bentuk akar di dalam akar terlebih dahulu, kemudian baru dilakukan perkalian sekawan seperti biasa. Proses ini dapat melibatkan beberapa kali iterasi penyederhanaan.
Contoh: Rasionalkan 1 / √(√2 + 1)
Penyelesaian: Pertama, sederhanakan bentuk akar di dalam akar. Kemudian rasionalkan penyebutnya:
1 / √(√2 + 1) = 1 / √[(√2 + 1)(√2 -1)/(√2 -1)] = √(√2 – 1) / √(2 – 1) = √(√2 – 1)
Merasionalkan Bentuk Akar dengan Penyederhanaan Aljabar Terlebih Dahulu
Beberapa soal memerlukan penyederhanaan aljabar sebelum merasionalkan bentuk akar. Penyederhanaan ini dapat meliputi faktorisasi, pengelompokan suku, atau penggunaan identitas aljabar lainnya untuk menyederhanakan bentuk akar sebelum proses merasionalkan dilakukan.
Contoh: Rasionalkan (√x + √y) / (x – y)
Penyelesaian: Gunakan identitas a²
-b² = (a+b)(a-b) untuk menyederhanakan penyebut:
(√x + √y) / (x – y) = (√x + √y) / (√x + √y)(√x – √y) = 1 / (√x – √y)
Kemudian, rasionalkan penyebut dengan mengalikan pembilang dan penyebut dengan sekawan penyebut (√x + √y):
1 / (√x – √y) = (√x + √y) / (x – y)
Penerapan Merasionalkan Bentuk Akar: Merasionalkan Bentuk Akar Kelas 10

Merasionalkan bentuk akar, meskipun terlihat seperti prosedur matematika yang abstrak, memiliki penerapan yang luas dan penting dalam berbagai bidang, mulai dari geometri dan fisika hingga permasalahan sehari-hari. Kemampuan untuk menyederhanakan bentuk akar dengan merasionalkan penyebutnya sangat krusial untuk mendapatkan hasil perhitungan yang akurat dan efisien. Berikut beberapa contoh penerapannya.
Penerapan Merasionalkan Bentuk Akar dalam Geometri
Dalam geometri, merasionalkan bentuk akar seringkali dibutuhkan untuk menghitung panjang sisi, luas, atau volume bangun geometri yang melibatkan akar. Misalnya, saat menghitung panjang diagonal suatu persegi atau panjang sisi segitiga siku-siku dengan menggunakan teorema Pythagoras, seringkali kita akan mendapatkan hasil berupa bentuk akar yang perlu dirasionalkan untuk mendapatkan nilai yang lebih akurat dan mudah dipahami.
Penerapan Merasionalkan Bentuk Akar dalam Fisika
Dalam fisika, banyak rumus dan persamaan yang melibatkan bentuk akar. Misalnya, dalam perhitungan kecepatan, percepatan, atau energi, kita seringkali menemukan bentuk akar yang perlu dirasionalkan untuk mendapatkan hasil yang presisi. Contohnya, dalam menghitung kecepatan suatu benda yang bergerak dengan percepatan konstan, rumus yang digunakan mungkin mengandung bentuk akar yang perlu dirasionalkan untuk mendapatkan nilai kecepatan yang akurat.
Penerapan Merasionalkan Bentuk Akar dalam Kehidupan Sehari-hari
Meskipun mungkin tidak disadari, merasionalkan bentuk akar juga memiliki penerapan dalam kehidupan sehari-hari. Contohnya, dalam perencanaan konstruksi bangunan, perhitungan luas lahan, atau bahkan dalam desain interior, merasionalkan bentuk akar dapat membantu dalam mendapatkan hasil perhitungan yang lebih akurat dan efisien. Akurasi dalam perhitungan ini sangat penting untuk menghindari kesalahan dan memastikan efisiensi dalam penggunaan material.
Ilustrasi Perhitungan Panjang Diagonal Persegi
Misalkan kita memiliki sebuah persegi dengan panjang sisi 2 cm. Untuk menghitung panjang diagonalnya, kita dapat menggunakan teorema Pythagoras. Teorema Pythagoras menyatakan bahwa kuadrat panjang sisi miring (diagonal) sama dengan jumlah kuadrat panjang kedua sisi lainnya. Dalam kasus persegi, panjang kedua sisi sama. Maka, panjang diagonal (d) dapat dihitung dengan rumus:
d = √(2² + 2²) = √8
Bentuk akar √8 dapat dirasionalkan menjadi 2√2 cm. Dengan merasionalkan bentuk akar, kita mendapatkan hasil yang lebih sederhana dan mudah dipahami, yaitu 2√2 cm, dibandingkan dengan √8 cm. Nilai 2√2 cm ini memberikan representasi panjang diagonal yang lebih akurat dan praktis dalam perhitungan selanjutnya.
Contoh Soal Cerita, Merasionalkan bentuk akar kelas 10
Sebuah tangga bersandar pada dinding dengan sudut kemiringan tertentu. Ujung bawah tangga berada 3 meter dari dinding, dan ujung atas tangga mencapai ketinggian 4 meter di dinding. Berapakah panjang tangga tersebut? Untuk menyelesaikan soal ini, kita dapat menggunakan teorema Pythagoras dan merasionalkan bentuk akar yang dihasilkan. Panjang tangga (L) dapat dihitung sebagai berikut:
L = √(3² + 4²) = √25 = 5 meter
Dalam contoh ini, meskipun tidak diperlukan merasionalkan bentuk akar karena hasilnya sudah berupa bilangan bulat, prinsip merasionalkan bentuk akar tetap relevan jika hasil perhitungan menghasilkan bentuk akar yang lebih kompleks.
Soal Latihan dan Pembahasan
Setelah mempelajari konsep merasionalkan bentuk akar, mari kita uji pemahaman kita melalui beberapa soal latihan. Soal-soal berikut disusun dengan variasi tingkat kesulitan untuk mengasah kemampuan kalian dalam merasionalkan berbagai bentuk akar.
Pembahasan setiap soal akan disajikan secara detail dan sistematis, mencakup langkah-langkah penyelesaian dan penjelasan konsep yang relevan. Hal ini diharapkan dapat membantu kalian memahami proses merasionalkan bentuk akar dengan lebih baik dan mengidentifikasi potensi kesalahan yang sering terjadi.
Soal Latihan Merasionalkan Bentuk Akar
Berikut lima soal latihan merasionalkan bentuk akar dengan tingkat kesulitan yang bervariasi. Cobalah selesaikan soal-soal ini sebelum melihat pembahasannya. Upayakan untuk memahami setiap langkah penyelesaian, bukan hanya sekedar mendapatkan jawaban akhir.
- Rasionalkan bentuk akar √(2/3).
- Sederhanakan bentuk akar √12 + √27 – √48.
- Rasionalkan bentuk akar (5 – √3)/(2 + √3).
- Tentukan nilai dari (√5 + √2)(√5 – √2).
- Rasionalkan penyebut dari 3/(√5 – 2).
Pembahasan Soal Latihan
Pembahasan berikut disajikan secara point-wise untuk memudahkan pemahaman. Setiap poin menjelaskan langkah-langkah penyelesaian secara rinci dan sistematis.
- Soal 1: Rasionalkan bentuk akar √(2/3).
- Kalikan pembilang dan penyebut dengan √3: √(2/3) x √3/√3 = √6/3
- Bentuk √6/3 sudah merupakan bentuk rasional.
- Soal 2: Sederhanakan bentuk akar √12 + √27 – √48.
- Faktorkan bilangan di dalam akar menjadi faktor kuadrat sempurna: √(4 x 3) + √(9 x 3)
-√(16 x 3) = 2√3 + 3√3 – 4√3 - Gabungkan suku-suku sejenis: 2√3 + 3√3 – 4√3 = √3
- Faktorkan bilangan di dalam akar menjadi faktor kuadrat sempurna: √(4 x 3) + √(9 x 3)
- Soal 3: Rasionalkan bentuk akar (5 – √3)/(2 + √3).
- Kalikan pembilang dan penyebut dengan sekawan penyebut (2 – √3): [(5 – √3)/(2 + √3)] x [(2 – √3)/(2 – √3)]
- Uraikan perkalian pada pembilang dan penyebut: (10 – 5√3 – 2√3 + 3) / (4 – 3)
- Sederhanakan: (13 – 7√3) / 1 = 13 – 7√3
- Soal 4: Tentukan nilai dari (√5 + √2)(√5 – √2).
- Ini merupakan perkalian bentuk (a + b)(a – b) = a²
-b² - Substitusikan a = √5 dan b = √2: (√5)²
-(√2)² = 5 – 2 = 3
- Ini merupakan perkalian bentuk (a + b)(a – b) = a²
- Soal 5: Rasionalkan penyebut dari 3/(√5 – 2).
- Kalikan pembilang dan penyebut dengan sekawan penyebut (√5 + 2): [3/(√5 – 2)] x [(√5 + 2)/(√5 + 2)]
- Uraikan perkalian pada pembilang dan penyebut: (3√5 + 6) / (5 – 4)
- Sederhanakan: 3√5 + 6
Tips dan Trik Merasionalkan Bentuk Akar
Merasionalkan bentuk akar pada dasarnya adalah menghilangkan akar dari penyebut suatu pecahan. Ingat selalu untuk mengalikan pembilang dan penyebut dengan sekawan penyebut untuk merasionalkan pecahan yang penyebutnya mengandung bentuk (a + √b) atau (a – √b). Perhatikan juga faktorisasi bilangan di dalam akar untuk menyederhanakan bentuk akar. Latihan yang konsisten akan meningkatkan pemahaman dan kemampuan kalian.
Kesimpulan Akhir
Dengan memahami konsep dan metode merasionalkan bentuk akar, siswa kelas 10 dapat dengan percaya diri menyelesaikan berbagai soal matematika yang melibatkan bentuk akar. Kemampuan ini tidak hanya penting untuk ujian, tetapi juga bermanfaat dalam berbagai bidang studi lain dan bahkan dalam kehidupan sehari-hari. Semoga panduan ini membantu dalam memahami dan menguasai teknik merasionalkan bentuk akar dengan lebih baik.