Persamaan kuadrat yang akar akarnya dan 2 adalah – Persamaan kuadrat yang akar-akarnya 2 dan x menyimpan misteri matematika yang menarik untuk diungkap. Memahami bagaimana menentukan persamaan kuadrat berdasarkan akar-akarnya, khususnya jika salah satunya sudah diketahui, merupakan kunci untuk menyelesaikan berbagai permasalahan matematika, bahkan yang diaplikasikan dalam soal cerita. Kita akan menjelajahi berbagai teknik dan contoh untuk menguasai konsep ini.
Topik ini akan membahas secara rinci bagaimana membentuk persamaan kuadrat jika salah satu akarnya adalah 2, dan bagaimana menentukan akar lainnya atau bahkan persamaan itu sendiri berdasarkan informasi tambahan seperti jumlah, hasil kali, atau selisih akar-akarnya. Kita juga akan melihat penerapannya dalam soal cerita dan hubungan mendalam antara akar-akar dengan koefisien persamaan kuadrat.
Persamaan Kuadrat dengan Akar-akar 2 dan x

Persamaan kuadrat merupakan suatu persamaan polinomial berderajat dua yang dapat ditulis dalam bentuk umum ax² + bx + c = 0, dengan a, b, dan c merupakan konstanta dan a ≠ 0. Akar-akar persamaan kuadrat adalah nilai-nilai x yang memenuhi persamaan tersebut. Dalam konteks ini, kita akan membahas persamaan kuadrat yang memiliki akar-akar 2 dan x, di mana x merupakan variabel.
Kita akan mengeksplorasi bagaimana membentuk persamaan tersebut, menganalisis kondisi agar akar-akarnya real, serta melihat hubungan antara koefisien dan akar-akarnya.
Bentuk Umum Persamaan Kuadrat
Jika akar-akar suatu persamaan kuadrat adalah α dan β, maka persamaan kuadrat tersebut dapat dinyatakan dalam bentuk (x – α)(x – β) = 0. Dalam kasus kita, α = 2 dan β = x. Oleh karena itu, bentuk umum persamaan kuadrat dengan akar-akar 2 dan x adalah (x – 2)(x – x) = 0. Namun, perlu diperhatikan bahwa bentuk ini akan menghasilkan persamaan x – 2 = 0 atau x = 2, yang hanya memiliki satu akar.
Untuk mendapatkan persamaan kuadrat yang sebenarnya, kita perlu mempertimbangkan bentuk umum yang lebih luas, yaitu k(x – 2)(x – x) = 0, dimana k adalah konstanta tak nol. Ini memberikan fleksibilitas dalam membentuk berbagai persamaan kuadrat dengan akar-akar yang diinginkan.
Contoh Persamaan Kuadrat
Berikut adalah tiga contoh persamaan kuadrat yang memiliki akar-akar 2 dan nilai x yang berbeda, dengan k=1, k=2 dan k= -1. Perlu diingat bahwa terdapat tak hingga banyak persamaan kuadrat yang memenuhi kondisi ini, karena nilai k dapat berupa bilangan real tak nol apapun.
- Jika k = 1 dan x = 3, persamaan kuadratnya adalah (x – 2)(x – 3) = 0, yang dapat disederhanakan menjadi x² – 5x + 6 = 0.
- Jika k = 2 dan x = -1, persamaan kuadratnya adalah 2(x – 2)(x + 1) = 0, yang dapat disederhanakan menjadi 2x²
2x – 4 = 0.
- Jika k = -1 dan x = 0, persamaan kuadratnya adalah -(x – 2)(x – 0) = 0, yang dapat disederhanakan menjadi -x² + 2x = 0.
Tabel Persamaan Kuadrat, Akar-akar, dan Diskriminan
Tabel berikut merangkum ketiga contoh persamaan kuadrat di atas, beserta akar-akar dan nilai diskriminannya (D = b²
-4ac).
| Persamaan Kuadrat | Akar-akar | Diskriminan (D) |
|---|---|---|
| x² – 5x + 6 = 0 | 2, 3 | 25 – 4(1)(6) = 1 |
2x²
|
2, -1 | 4 – 4(2)(-4) = 36 |
| -x² + 2x = 0 | 2, 0 | 4 – 4(-1)(0) = 4 |
Kondisi Akar-akar Real
Suatu persamaan kuadrat ax² + bx + c = 0 memiliki akar-akar real jika dan hanya jika diskriminannya (D = b²
-4ac) lebih besar dari atau sama dengan nol (D ≥ 0). Ini karena rumus kuadratik untuk mencari akar-akar persamaan kuadrat melibatkan akar kuadrat dari diskriminan. Jika diskriminan negatif, akar-akarnya akan berupa bilangan kompleks.
Hubungan Koefisien dan Akar-akar, Persamaan kuadrat yang akar akarnya dan 2 adalah
Untuk persamaan kuadrat ax² + bx + c = 0 dengan akar-akar α dan β, terdapat hubungan yang sederhana antara koefisien dan akar-akarnya. Secara khusus, jumlah akar-akarnya (α + β) sama dengan -b/a, dan hasil kali akar-akarnya (αβ) sama dengan c/a. Ilustrasi deskriptif: Bayangkan grafik parabola yang mewakili persamaan kuadrat. Titik potong parabola dengan sumbu x menunjukkan akar-akar persamaan.
Posisi titik potong ini, dan dengan demikian akar-akarnya, bergantung pada nilai a, b, dan c. Nilai a menentukan arah pembukaan parabola (ke atas jika a > 0, ke bawah jika a < 0) dan seberapa "terbuka" atau "sempit" parabolanya. Nilai b memengaruhi posisi sumbu simetri parabola, dan nilai c menentukan titik potong parabola dengan sumbu y. Dengan demikian, koefisien a, b, dan c secara langsung memengaruhi posisi dan bentuk parabola, yang pada gilirannya menentukan nilai akar-akarnya.
Menentukan Nilai Koefisien Persamaan Kuadrat
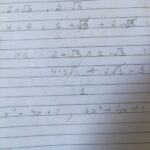
Menentukan persamaan kuadrat jika salah satu akarnya diketahui merupakan proses yang relatif mudah, terutama jika informasi tambahan mengenai akar lainnya diberikan. Dengan memanfaatkan sifat-sifat akar persamaan kuadrat, kita dapat membangun persamaan tersebut. Berikut beberapa contoh kasus dan langkah-langkah sistematisnya.
Menentukan Persamaan Kuadrat dengan Jumlah Akar-akar
Jika diketahui salah satu akar persamaan kuadrat adalah 2 dan jumlah akar-akarnya adalah 5, kita dapat menentukan akar kedua dan selanjutnya persamaan kuadratnya. Misalkan akar-akar persamaan kuadrat adalah α dan β. Karena α = 2 dan α + β = 5, maka β = 5 – 2 = 3. Dengan demikian, akar-akarnya adalah 2 dan 3. Persamaan kuadratnya dapat ditulis dalam bentuk (x – α)(x – β) = 0, sehingga (x – 2)(x – 3) = 0.
Setelah dikalikan, persamaan kuadratnya menjadi x²
-5x + 6 = 0.
Menentukan Persamaan Kuadrat dengan Hasil Kali Akar-akar
Jika diketahui salah satu akar persamaan kuadrat adalah 2 dan hasil kali akar-akarnya adalah 6, kita dapat menentukan akar kedua dan selanjutnya persamaan kuadratnya. Dengan menggunakan rumus hasil kali akar-akar (αβ = 6) dan mengetahui α = 2, maka β = 6/2 = 3. Persamaan kuadratnya adalah (x – 2)(x – 3) = 0, atau x²
-5x + 6 = 0.
Menentukan Persamaan Kuadrat dengan Selisih Akar-akar
Jika diketahui salah satu akar persamaan kuadrat adalah 2 dan selisih akar-akarnya adalah 3, terdapat dua kemungkinan pasangan akar. Jika α = 2 dan α
-β = 3, maka β = 2 – 3 = -1. Persamaan kuadratnya adalah (x – 2)(x + 1) = 0, atau x²
-x – 2 = 0. Sebaliknya, jika β = 2 dan β
-α = 3, maka α = 2 – 3 = -1.
Persamaan kuadratnya adalah (x + 1)(x – 2) = 0, atau x²
-x – 2 = 0. Dalam kasus ini, hanya terdapat satu persamaan kuadrat yang unik.
Contoh Soal dan Penyelesaian
Sebuah persamaan kuadrat memiliki salah satu akarnya 2 dan jumlah akar-akarnya 7. Tentukan persamaan kuadrat tersebut.
Penyelesaian: Misalkan akar-akarnya α dan β. Diketahui α = 2 dan α + β = 7. Maka β = 7 – 2 = 5. Persamaan kuadratnya adalah (x – 2)(x – 5) = 0, yang dapat disederhanakan menjadi x²
-7x + 10 = 0.
Langkah-langkah Sistematis Menentukan Persamaan Kuadrat
- Identifikasi informasi yang diketahui: Salah satu akar (misal α) dan hubungan antara akar-akar (jumlah, hasil kali, atau selisih).
- Gunakan informasi yang diketahui untuk menentukan akar kedua (β).
- Bentuk persamaan kuadrat dalam faktor (x – α)(x – β) = 0.
- Kalikan faktor-faktor tersebut untuk mendapatkan persamaan kuadrat dalam bentuk ax² + bx + c = 0.
Penerapan Persamaan Kuadrat dengan Akar 2
Persamaan kuadrat, selain memiliki aplikasi dalam berbagai bidang matematika, juga sering muncul dalam penyelesaian masalah di kehidupan nyata. Memahami bagaimana persamaan kuadrat, khususnya yang memiliki akar 2, dapat diterapkan dalam pemecahan masalah merupakan kunci untuk menguasai konsep ini secara komprehensif. Berikut beberapa contoh penerapannya dalam soal cerita.
Soal Cerita dan Penyelesaiannya
Sebuah taman berbentuk persegi panjang memiliki luas 50 meter persegi. Panjang taman tersebut 2 meter lebih panjang dari lebarnya. Tentukan panjang dan lebar taman tersebut.
Skenario: Bayangkan sebuah taman persegi panjang yang luasnya diketahui. Kita perlu mencari dimensi (panjang dan lebar) taman tersebut, dengan informasi tambahan mengenai hubungan antara panjang dan lebar.
Solusi: Misalkan lebar taman adalah x meter. Karena panjang 2 meter lebih panjang dari lebar, maka panjangnya adalah x + 2 meter. Luas taman adalah panjang kali lebar, sehingga kita dapat membentuk persamaan kuadrat:
x(x + 2) = 50
Dengan mengalikan dan menyederhanakan persamaan tersebut, kita peroleh:
x² + 2x – 50 = 0
Persamaan kuadrat ini dapat diselesaikan menggunakan rumus kuadrat atau faktorisasi. Salah satu akarnya adalah 2 (walaupun tidak terlihat langsung dari persamaan). Namun, kita akan menggunakan rumus kuadrat untuk mencari akar-akarnya:
Dengan a = 1, b = 2, dan c = -50, kita substitusikan nilai-nilai tersebut ke dalam rumus kuadrat. Setelah perhitungan, kita akan mendapatkan dua akar, salah satunya adalah x ≈ 6.56. Karena x mewakili lebar, maka lebar taman kira-kira 6.56 meter. Panjangnya adalah x + 2 ≈ 8.56 meter.
Perlu dicatat bahwa akar lainnya akan bernilai negatif, yang tidak mungkin untuk panjang atau lebar taman. Oleh karena itu, kita hanya mengambil akar positif.
Contoh Soal Cerita Lainnya
Sebuah proyektil diluncurkan vertikal ke atas dengan kecepatan awal 20 m/s. Tinggi proyektil (h) setelah t detik dirumuskan dengan persamaan h = -5t² + 20t. Pada saat berapakah proyektil mencapai ketinggian 15 meter?
Skenario: Bayangkan sebuah proyektil yang diluncurkan ke atas, lintasannya mengikuti persamaan kuadrat. Kita perlu menentukan waktu ketika proyektil berada pada ketinggian tertentu.
Solusi: Kita substitusikan h = 15 ke dalam persamaan: 15 = -5t² + 20t. Kemudian, kita atur persamaan menjadi bentuk standar persamaan kuadrat:
5t² – 20t + 15 = 0
Kita dapat menyederhanakan persamaan dengan membagi semua suku dengan 5:
t² – 4t + 3 = 0
Persamaan ini dapat difaktorkan menjadi (t – 1)(t – 3) = 0. Akar-akarnya adalah t = 1 dan t = 3. Ini berarti proyektil mencapai ketinggian 15 meter pada detik ke-1 dan detik ke-3 (saat naik dan saat turun).
Tipe Soal Cerita yang Dapat Diselesaikan
Persamaan kuadrat dengan akar 2, atau lebih umum, persamaan kuadrat sering digunakan untuk memodelkan berbagai situasi dalam kehidupan nyata. Beberapa tipe soal cerita yang dapat diselesaikan dengan persamaan kuadrat meliputi:
- Masalah yang berkaitan dengan luas dan keliling bangun geometri (persegi panjang, persegi).
- Masalah gerak parabola (seperti peluru atau bola yang dilempar).
- Masalah yang melibatkan pertumbuhan atau penurunan eksponensial (dengan pendekatan kuadrat).
- Masalah optimasi (mencari nilai maksimum atau minimum).
Hubungan Akar-akar dan Koefisien: Persamaan Kuadrat Yang Akar Akarnya Dan 2 Adalah

Persamaan kuadrat memiliki hubungan yang erat antara akar-akarnya dan koefisien-koefisiennya. Memahami hubungan ini sangat penting dalam menyelesaikan persamaan kuadrat dan memecahkan berbagai masalah matematika yang melibatkan persamaan kuadrat. Jika kita mengetahui salah satu akarnya, kita dapat menggunakan hubungan ini untuk menemukan akar lainnya dengan lebih mudah.
Secara umum, persamaan kuadrat ditulis dalam bentuk ax² + bx + c = 0, di mana a, b, dan c adalah koefisien konstanta, dan x mewakili variabel. Akar-akar persamaan ini, yang kita sebut α dan β, merupakan nilai-nilai x yang memenuhi persamaan tersebut. Hubungan antara akar-akar dan koefisien ini akan dijelaskan lebih lanjut.
Rumus Penjumlahan dan Perkalian Akar-akar
Terdapat dua rumus utama yang menghubungkan akar-akar persamaan kuadrat dengan koefisiennya: rumus penjumlahan akar-akar dan rumus perkalian akar-akar. Rumus-rumus ini berlaku untuk semua persamaan kuadrat, termasuk kasus di mana salah satu akarnya diketahui.
- Penjumlahan akar-akar (α + β): α + β = -b/a
- Perkalian akar-akar (αβ): αβ = c/a
Penerapan Rumus pada Kasus Salah Satu Akarnya 2
Misalkan kita memiliki persamaan kuadrat dengan salah satu akarnya adalah 2 (misal α = 2). Dengan menggunakan rumus di atas, kita dapat menentukan akar lainnya (β) jika koefisien a, b, dan c diketahui. Kita hanya perlu mensubstitusikan nilai α = 2 ke dalam rumus penjumlahan dan perkalian akar-akar, lalu menyelesaikan persamaan yang terbentuk.
Contoh Numerik
Mari kita ilustrasikan dengan beberapa contoh. Misalkan kita memiliki persamaan kuadrat x²
-5x + 6 =
0. Dari persamaan ini, kita tahu bahwa a = 1, b = -5, dan c =
6. Jika salah satu akarnya adalah 2 (α = 2), kita dapat menemukan akar lainnya (β) sebagai berikut:
- Penjumlahan akar-akar: 2 + β = -(-5)/1 = 5. Oleh karena itu, β = 5 – 2 = 3.
- Perkalian akar-akar: 2β = 6/1 = 6. Oleh karena itu, β = 6/2 = 3.
Jadi, akar-akar persamaan x²
-5x + 6 = 0 adalah 2 dan 3.
Contoh lain: Jika persamaan kuadratnya adalah 2x²
-7x + 6 = 0 dan salah satu akarnya adalah 2, maka:
- Penjumlahan akar-akar: 2 + β = -(-7)/2 = 3.5. Oleh karena itu, β = 3.5 – 2 = 1.5
- Perkalian akar-akar: 2β = 6/2 = 3. Oleh karena itu, β = 3/2 = 1.5
Akar-akar persamaan 2x²
-7x + 6 = 0 adalah 2 dan 1.5
Kemudahan dalam Penyelesaian Masalah
Dengan memahami hubungan antara akar-akar dan koefisien, kita dapat menyederhanakan proses penyelesaian masalah yang berkaitan dengan persamaan kuadrat. Mengetahui salah satu akarnya, kita dapat dengan cepat menemukan akar lainnya tanpa perlu menggunakan rumus kuadratik atau metode pemfaktoran yang lebih rumit. Ini sangat membantu dalam situasi di mana kita hanya membutuhkan satu akar, atau jika metode lain terbukti terlalu kompleks.
Kesimpulan Akhir
Memahami hubungan antara akar-akar dan koefisien persamaan kuadrat, khususnya ketika salah satu akarnya diketahui, membuka pintu menuju pemecahan masalah yang lebih efisien. Dengan menguasai teknik-teknik yang telah dibahas, kita dapat dengan mudah menentukan persamaan kuadrat yang sesuai, serta menyelesaikan berbagai soal cerita yang melibatkan konsep ini. Kemampuan ini tak hanya penting dalam matematika, tetapi juga berguna dalam berbagai bidang ilmu pengetahuan dan teknologi yang bergantung pada model matematika.