Soal perpangkatan dan bentuk akar kelas 9 merupakan bagian penting matematika yang menguji pemahaman tentang eksponen, akar, dan penerapannya dalam berbagai konteks. Materi ini membangun fondasi yang kuat untuk aljabar tingkat lanjut. Memahami konsep perpangkatan dan bentuk akar, termasuk sifat-sifat dan operasi hitungnya, sangat krusial untuk menyelesaikan berbagai jenis soal, mulai dari soal hitung sederhana hingga soal cerita yang lebih kompleks dan menantang.
Bab ini akan membahas secara rinci definisi perpangkatan dan bentuk akar, sifat-sifatnya, operasi hitung yang melibatkan keduanya, serta penerapannya dalam penyelesaian masalah kontekstual. Dengan pemahaman yang komprehensif, siswa akan mampu menguasai berbagai tipe soal, termasuk soal yang menggabungkan perpangkatan dan bentuk akar, serta soal yang membutuhkan penggunaan identitas aljabar.
Pengertian Perpangkatan dan Bentuk Akar: Soal Perpangkatan Dan Bentuk Akar Kelas 9
Perpangkatan dan bentuk akar merupakan dua konsep matematika yang saling berkaitan erat. Pemahaman yang baik tentang keduanya sangat penting dalam menyelesaikan berbagai permasalahan matematika, terutama di tingkat lanjut. Keduanya merupakan operasi matematika yang melibatkan bilangan pokok (basis) dan eksponen (pangkat) atau indeks (untuk akar).
Definisi Perpangkatan dan Bentuk Akar
Perpangkatan didefinisikan sebagai perkalian berulang suatu bilangan (basis) sebanyak bilangan tertentu (eksponen). Secara umum, perpangkatan ditulis sebagai a n, di mana ‘a’ adalah basis dan ‘n’ adalah eksponen. Jika n adalah bilangan bulat positif, maka a n = a × a × a × … × a (sebanyak n kali). Sementara itu, bentuk akar merupakan kebalikan dari perpangkatan.
Bentuk akar √ na dibaca sebagai akar pangkat n dari a, di mana ‘a’ adalah bilangan yang diakarkan dan ‘n’ adalah indeks akar. Bentuk akar ini mencari bilangan yang jika dipangkatkan n akan menghasilkan a. Jika n=2, maka disebut akar kuadrat dan sering ditulis sebagai √a.
Contoh Soal Perpangkatan
Berikut beberapa contoh soal perpangkatan dengan basis dan eksponen yang berbeda:
- 2 3 = 2 × 2 × 2 = 8
- 5 2 = 5 × 5 = 25
- (-3) 4 = (-3) × (-3) × (-3) × (-3) = 81
- (1/2) 3 = (1/2) × (1/2) × (1/2) = 1/8
Contoh Soal Bentuk Akar
Berikut beberapa contoh soal bentuk akar dengan berbagai jenis operasi:
- √25 = 5 karena 5 2 = 25
- √64 = 8 karena 8 2 = 64
- ∛8 = 2 karena 2 3 = 8
- √16 + √9 = 4 + 3 = 7
- √(25 × 4) = √100 = 10
Perbandingan Perpangkatan dan Bentuk Akar
Tabel berikut menunjukkan perbandingan antara perpangkatan dan bentuk akar, termasuk sifat-sifatnya:
| Jenis Operasi | Rumus | Contoh Soal | Penjelasan |
|---|---|---|---|
| Perpangkatan | an | 34 = 81 | Basis 3 dipangkatkan 4 (dikalikan sebanyak 4 kali). |
| Bentuk Akar | √na | √364 = 4 | Mencari bilangan yang jika dipangkatkan 3 hasilnya 64. |
| Perpangkatan dengan eksponen negatif | a-n = 1/an | 2-2 = 1/4 | Eksponen negatif menunjukkan kebalikan dari perpangkatan positif. |
| Bentuk akar dengan indeks pecahan | √m/na = (√na)m | √2/38 = (∛8)2 = 22 = 4 | Indeks pecahan menunjukkan kombinasi perpangkatan dan bentuk akar. |
Contoh Soal Cerita Perpangkatan dan Bentuk Akar
Sebuah kolam renang berbentuk kubus memiliki volume 64 meter kubik. Berapa panjang sisi kolam renang tersebut?
Penyelesaian: Volume kubus = sisi 3. Karena volume 64 m 3, maka sisi 3 = 64. Dengan demikian, panjang sisi kolam renang adalah ∛64 = 4 meter.
Sifat-Sifat Perpangkatan dan Bentuk Akar
Bab ini akan membahas sifat-sifat perpangkatan dan bentuk akar yang sangat penting dalam aljabar. Memahami sifat-sifat ini akan memudahkan kalian dalam menyelesaikan berbagai soal matematika, khususnya yang melibatkan eksponen dan radikal.
Sifat-Sifat Perpangkatan
Perpangkatan merupakan operasi matematika yang melibatkan perkalian berulang suatu bilangan. Pemahaman atas sifat-sifat perpangkatan sangat krusial untuk menyelesaikan persamaan dan soal-soal yang lebih kompleks. Berikut beberapa sifat pentingnya:
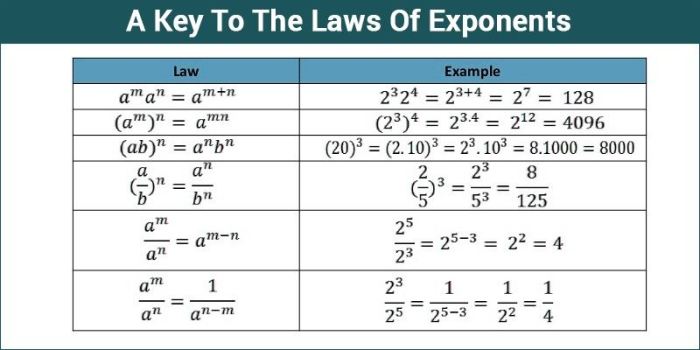
- Perkalian Perpangkatan dengan Basis Sama: a m × a n = a m+n. Misalnya, 2 3 × 2 2 = 2 3+2 = 2 5 = 32.
- Pembagian Perpangkatan dengan Basis Sama: a m ÷ a n = a m-n (dengan syarat a ≠ 0). Misalnya, 3 5 ÷ 3 2 = 3 5-2 = 3 3 = 27.
- Perpangkatan Berpangkat: (a m) n = a m×n. Misalnya, (5 2) 3 = 5 2×3 = 5 6 = 15625.
- Perkalian Perpangkatan dengan Eksponen Sama: (a × b) m = a m × b m. Misalnya, (2 × 3) 2 = 2 2 × 3 2 = 4 × 9 = 36.
- Pembagian Perpangkatan dengan Eksponen Sama: (a ÷ b) m = a m ÷ b m (dengan syarat b ≠ 0). Misalnya, (6 ÷ 2) 3 = 6 3 ÷ 2 3 = 216 ÷ 8 = 27.
Sifat-Sifat Bentuk Akar
Bentuk akar, atau radikal, merupakan kebalikan dari perpangkatan. Memahami sifat-sifat bentuk akar memungkinkan kita untuk menyederhanakan ekspresi dan menyelesaikan persamaan yang melibatkan akar. Berikut beberapa sifat pentingnya:
- Penyederhanaan Bentuk Akar: √(a × b) = √a × √b. Misalnya, √12 = √(4 × 3) = √4 × √3 = 2√3.
- Penjumlahan dan Pengurangan Bentuk Akar: Hanya bentuk akar sejenis (dengan angka di dalam akar yang sama) yang dapat dijumlahkan atau dikurangkan. Misalnya, 2√5 + 3√5 = 5√5, sedangkan 2√5 + 3√2 tidak dapat disederhanakan lebih lanjut.
- Perkalian Bentuk Akar: √a × √b = √(a × b). Misalnya, √2 × √8 = √(2 × 8) = √16 = 4.
- Pembagian Bentuk Akar: √a ÷ √b = √(a ÷ b) (dengan syarat b ≠ 0). Misalnya, √18 ÷ √2 = √(18 ÷ 2) = √9 = 3.
Contoh Penerapan Sifat Perpangkatan dan Bentuk Akar
Berikut contoh soal yang membutuhkan penggunaan lebih dari satu sifat perpangkatan dan bentuk akar:
Sederhanakanlah ekspresi berikut: (√12 × √3) 2 ÷ 2√27
- Sederhanakan √12: √12 = √(4 × 3) = 2√3
- Substitusikan ke dalam ekspresi: (2√3 × √3)2 ÷ 2√27
- Hitung perkalian di dalam kurung: (2 × 3) 2 ÷ 2√27 = 6 2 ÷ 2√27
- Hitung perpangkatan: 36 ÷ 2√27
- Sederhanakan √27: √27 = √(9 × 3) = 3√3
- Substitusikan dan hitung: 36 ÷ (2 × 3√3) = 36 ÷ 6√3 = 6 ÷ √3
- Rasionalkan penyebut: (6 ÷ √3) × (√3 ÷ √3) = 6√3 ÷ 3 = 2√3
Jadi, penyederhanaan ekspresi (√12 × √3) 2 ÷ 2√27 adalah 2√3.
Operasi Hitung pada Perpangkatan dan Bentuk Akar
Bab ini akan membahas operasi hitung pada perpangkatan dan bentuk akar, mencakup penyelesaian soal perpangkatan dengan berbagai jenis bilangan dan penyederhanaan bentuk akar dengan berbagai operasi. Pemahaman yang kuat tentang operasi ini sangat penting untuk menyelesaikan soal-soal matematika yang lebih kompleks di tingkat selanjutnya.
Perpangkatan dengan Berbagai Jenis Bilangan
Perpangkatan melibatkan perkalian berulang suatu bilangan (basis) sebanyak pangkat yang ditentukan. Proses ini dapat diterapkan pada bilangan bulat, pecahan, dan desimal. Langkah-langkah penyelesaiannya pada dasarnya sama, hanya berbeda dalam perhitungannya.
- Bilangan Bulat: Misalnya, 2 3 = 2 × 2 × 2 = 8. Perkalian berulang angka 2 sebanyak tiga kali.
- Pecahan: Misalnya, (½) 2 = (½) × (½) = ¼. Perkalian berulang pecahan ½ sebanyak dua kali.
- Desimal: Misalnya, (0.5) 3 = 0.5 × 0.5 × 0.5 = 0.125. Perkalian berulang desimal 0.5 sebanyak tiga kali.
Perlu diingat aturan-aturan perpangkatan seperti perkalian dan pembagian basis yang sama, serta perpangkatan bertingkat, untuk memudahkan penyelesaian soal yang lebih kompleks.
Penyederhanaan Bentuk Akar
Bentuk akar merupakan representasi dari suatu bilangan yang jika dikuadratkan menghasilkan bilangan tersebut. Penyederhanaan bentuk akar bertujuan untuk menyajikan bentuk akar dalam bentuk yang paling sederhana. Hal ini melibatkan beberapa langkah, termasuk faktorisasi dan pengelompokan.
- Faktorisasi: Cari faktor-faktor dari bilangan dalam akar kuadrat yang merupakan kuadrat sempurna. Misalnya, √12 = √(4 × 3) = √4 × √3 = 2√3.
- Pengelompokan: Untuk bentuk akar yang lebih kompleks, kelompokkan faktor-faktor yang merupakan kuadrat sempurna. Misalnya, √(75x 3) = √(25x 2 × 3x) = 5x√(3x).
- Rasionalisasi: Proses menghilangkan bentuk akar pada penyebut pecahan. Misalnya, untuk merasionalisasi 1/√2, kita kalikan pembilang dan penyebut dengan √2, sehingga menjadi √2/2.
Contoh Soal Operasi Hitung pada Bentuk Akar
Berikut beberapa contoh soal yang melibatkan operasi penjumlahan, pengurangan, perkalian, dan pembagian pada bentuk akar:
- 2√3 + 3√3 = 5√3
- 5√2 – 2√2 = 3√2
- (√2)(√8) = √16 = 4
- √18 / √2 = √(18/2) = √9 = 3
Contoh Soal Gabungan Perpangkatan dan Bentuk Akar
Soal berikut menggabungkan konsep perpangkatan dan bentuk akar:
Hitunglah nilai dari (√2) 4 + 2√8 – √18
Penyelesaian:
- (√2)4 = (√2 × √2 × √2 × √2) = 4
- 2√8 = 2√(4 × 2) = 2(2√2) = 4√2
- √18 = √(9 × 2) = 3√2
- Jadi, (√2) 4 + 2√8 – √18 = 4 + 4√2 – 3√2 = 4 + √2
Strategi Umum Penyelesaian Soal Kompleks
Untuk menyelesaikan soal perpangkatan dan bentuk akar yang kompleks, penting untuk memahami sifat-sifat perpangkatan dan bentuk akar, serta menguasai teknik-teknik penyederhanaan. Identifikasi bagian-bagian soal yang dapat disederhanakan terlebih dahulu, lalu terapkan operasi hitung sesuai dengan urutan operasi yang benar (prioritas operasi). Periksa kembali hasil akhir untuk memastikan kebenarannya.
Penerapan Perpangkatan dan Bentuk Akar dalam Masalah Kontekstual
Perpangkatan dan bentuk akar, meskipun tampak abstrak, memiliki aplikasi luas dalam kehidupan sehari-hari. Memahami konsep ini memungkinkan kita untuk menyelesaikan berbagai permasalahan yang melibatkan perhitungan luas, volume, skala, dan bahkan pertumbuhan populasi. Berikut beberapa contoh penerapannya dalam konteks yang lebih nyata dan mudah dipahami.
Soal Cerita dan Penyelesaiannya
Berikut tiga soal cerita yang mengaplikasikan konsep perpangkatan dan bentuk akar, beserta petunjuk penyelesaian dan solusi lengkapnya. Soal-soal ini dirancang untuk menunjukkan fleksibilitas dan kegunaan perpangkatan dan bentuk akar dalam berbagai situasi.
- Soal 1: Luas Taman Kota
Sebuah taman kota berbentuk persegi memiliki luas 1225 meter persegi. Berapakah panjang sisi taman tersebut? - Soal 2: Volume Kubus
Sebuah kubus memiliki volume 2197 cm³. Berapakah panjang rusuk kubus tersebut? - Soal 3: Pertumbuhan Populasi Bakteri
Populasi bakteri tertentu berkembang biak dengan cara membelah diri. Jika awalnya terdapat 100 bakteri dan populasi bakteri tersebut meningkat menjadi 100 x 2 4 setelah 4 jam, berapakah jumlah bakteri setelah 4 jam?
Petunjuk dan Solusi Soal Cerita
Berikut petunjuk penyelesaian dan solusi untuk masing-masing soal cerita di atas. Pemahaman langkah-langkah ini akan membantu Anda dalam menyelesaikan permasalahan serupa di masa mendatang.
- Soal 1: Luas Taman Kota
Petunjuk: Karena taman berbentuk persegi, luasnya adalah sisi x sisi. Ambil akar kuadrat dari luas untuk mencari panjang sisi.
Solusi: √1225 = 35 meter. Panjang sisi taman kota adalah 35 meter. - Soal 2: Volume Kubus
Petunjuk: Volume kubus adalah rusuk x rusuk x rusuk (rusuk³). Ambil akar pangkat tiga dari volume untuk mencari panjang rusuk.
Solusi: ³√2197 = 13 cm. Panjang rusuk kubus adalah 13 cm. - Soal 3: Pertumbuhan Populasi Bakteri
Petunjuk: Hitung nilai 2 4 terlebih dahulu, lalu kalikan dengan jumlah bakteri awal.
Solusi: 2 4 = 16. Jumlah bakteri setelah 4 jam adalah 100 x 16 = 1600 bakteri.
Ilustrasi Deskriptif Soal Luas Taman Kota
Bayangkan sebuah taman kota yang luas dan rapi, berbentuk bujur sangkar sempurna. Rumputnya terawat dengan baik, dan bunga-bunga beraneka warna menghiasi tepiannya. Luas keseluruhan taman ini diketahui sebesar 1225 meter persegi. Untuk merencanakan penataan taman lebih lanjut, seperti penempatan bangku, jalur pejalan kaki, dan area bermain anak, kita perlu mengetahui panjang setiap sisi taman. Dengan menggunakan konsep akar kuadrat, kita dapat menghitung panjang sisi taman tersebut, yang akan menjadi dasar perencanaan tata ruang yang efektif dan efisien.
Jenis-jenis Soal Cerita yang Umum Ditemukan, Soal perpangkatan dan bentuk akar kelas 9
Soal cerita yang melibatkan perpangkatan dan bentuk akar seringkali muncul dalam konteks geometri (luas dan volume bangun ruang), fisika (perhitungan jarak dan kecepatan), dan biologi (pertumbuhan populasi). Selain itu, soal-soal yang melibatkan skala peta, perhitungan bunga majemuk, dan perhitungan energi juga seringkali menggunakan konsep ini.
Soal Latihan dan Pembahasan
Berikut beberapa soal latihan untuk menguji pemahaman Anda tentang perpangkatan dan bentuk akar, disertai pembahasan lengkapnya. Soal-soal ini dirancang dengan variasi tingkat kesulitan untuk mengasah kemampuan Anda secara menyeluruh. Setelah mengerjakan soal latihan, perhatikan pula ringkasan rumus dan sifat penting yang disajikan dalam tabel.
Soal Latihan Perpangkatan dan Bentuk Akar
Soal-soal berikut ini menguji kemampuan dalam mengoperasikan bilangan berpangkat dan bentuk akar, mulai dari yang sederhana hingga yang lebih kompleks yang melibatkan manipulasi aljabar.
- Sederhanakan bentuk
√75
- Hitunglah nilai dari
23 x 2 -2
- Sederhanakan bentuk
(√5 + √2)(√5 – √2)
- Tentukan nilai x yang memenuhi persamaan
x 2 = 16
- Sederhanakan bentuk
√12x 3y 4
Pembahasan Soal Latihan
Berikut pembahasan lengkap untuk setiap soal latihan di atas. Pembahasan ini bertujuan untuk memberikan pemahaman yang komprehensif tentang langkah-langkah penyelesaian.
-
√75 = √(25 x 3) = √25 x √3 = 5√3
-
23 x 2 -2 = 2 3+(-2) = 2 1 = 2
-
(√5 + √2)(√5 – √2) = (√5) 2
-(√2) 2 = 5 – 2 = 3Ini merupakan penerapan dari rumus selisih kuadrat (a+b)(a-b) = a 2 – b 2
-
x 2 = 16 maka x = ±√16 = ±4
Perlu diperhatikan bahwa persamaan kuadrat memiliki dua akar, yaitu 4 dan -4.
-
√12x 3y 4 = √(4 x 3 x x 2 x x x y 4) = √4 x √x 2 x √y 4 x √(3x) = 2xy 2√(3x)
Tabel Ringkasan Rumus dan Sifat Penting
Tabel berikut merangkum rumus dan sifat penting yang berkaitan dengan perpangkatan dan bentuk akar. Tabel ini dirancang untuk memudahkan Anda dalam mengingat dan memahami konsep-konsep kunci.
| Rumus/Sifat | Penjelasan | Contoh | Catatan |
|---|---|---|---|
| am x an = am+n | Perkalian bilangan berpangkat dengan basis sama | 23 x 22 = 25 = 32 | Basis harus sama |
| am / an = am-n | Pembagian bilangan berpangkat dengan basis sama | 34 / 32 = 32 = 9 | Basis harus sama |
| (am)n = am x n | Perpangkatan bilangan berpangkat | (23)2 = 26 = 64 | – |
| √(a x b) = √a x √b | Sifat perkalian bentuk akar | √(9 x 4) = √9 x √4 = 3 x 2 = 6 | a dan b ≥ 0 |
| √(a/b) = √a / √b | Sifat pembagian bentuk akar | √(9/4) = √9 / √4 = 3/2 | a ≥ 0 dan b > 0 |
| a0 = 1 (a ≠ 0) | Bilangan berpangkat nol | 50 = 1 | – |
| a-n = 1/an (a ≠ 0) | Bilangan berpangkat negatif | 2-2 = 1/22 = 1/4 | – |
Contoh Soal Penyederhanaan Bentuk Akar dengan Koefisien dan Variabel
Berikut contoh soal yang melibatkan penyederhanaan bentuk akar dengan koefisien dan variabel, yang memerlukan pemahaman mendalam tentang sifat-sifat akar dan perpangkatan.
Sederhanakan bentuk
3√(8x 4y 6)
Penyelesaian: 3√(8x 4y 6) = 3√(2 3x 4y 6) = 3 x 2x 2y 3 = 6x 2y 3
Contoh Soal Menggunakan Identitas Aljabar
Berikut contoh soal yang membutuhkan penggunaan identitas aljabar dalam penyelesaiannya. Kemampuan mengaplikasikan identitas aljabar sangat penting dalam menyelesaikan soal-soal perpangkatan dan bentuk akar yang lebih kompleks.
Sederhanakan (x + √y) 2
Penyelesaian: (x + √y) 2 = x 2 + 2x√y + y. Ini menggunakan identitas aljabar (a + b) 2 = a 2 + 2ab + b 2
Pemungkas
Menguasai perpangkatan dan bentuk akar merupakan kunci keberhasilan dalam matematika kelas 9 dan seterusnya. Dengan memahami konsep dasar, sifat-sifat, dan berbagai teknik penyelesaian soal, siswa dapat meningkatkan kemampuan pemecahan masalah dan membangun kepercayaan diri dalam menghadapi tantangan matematika yang lebih kompleks. Latihan soal secara rutin dan pemahaman yang mendalam akan membantu siswa menguasai materi ini dengan baik.