- Memahami Pecahan Biasa dan Campuran
-
Mengubah Pecahan Biasa Menjadi Pecahan Campuran: Tuliskan Bentuk Pecahan Campuran Dari Pecahan Berikut
- Langkah-Langkah Mengubah Pecahan Biasa Menjadi Pecahan Campuran
- Contoh Prosedur Perubahan Pecahan Biasa Menjadi Pecahan Campuran
- Contoh Soal dan Penyelesaian Mengubah Pecahan Biasa Menjadi Pecahan Campuran
- Menentukan Bagian Bulat dan Sisa dari Pecahan Biasa
- Contoh Soal dengan Tingkat Kesulitan Berbeda
-
Mengenali Syarat Pecahan yang Dapat Diubah Menjadi Pecahan Campuran
- Contoh Pecahan yang Dapat dan Tidak Dapat Diubah Menjadi Pecahan Campuran
- Penjelasan Mengapa Pecahan dengan Pembilang Lebih Kecil dari Penyebut Tidak Dapat Diubah Menjadi Pecahan Campuran, Tuliskan bentuk pecahan campuran dari pecahan berikut
- Karakteristik Pecahan Biasa yang Memungkinkan Konversi ke Pecahan Campuran
- Contoh Soal Identifikasi Kemungkinan Konversi ke Pecahan Campuran
- Penerapan Pecahan Campuran dalam Kehidupan Sehari-hari
- Kesimpulan Akhir
Tuliskan bentuk pecahan campuran dari pecahan berikut merupakan topik yang penting dalam memahami konsep pecahan. Pecahan campuran, dengan kombinasi bilangan bulat dan pecahan biasa, seringkali lebih mudah dipahami dan diaplikasikan dalam kehidupan sehari-hari dibandingkan dengan pecahan biasa yang bernilai besar. Memahami cara mengubah pecahan biasa menjadi pecahan campuran dan sebaliknya merupakan kunci untuk menguasai operasi matematika yang melibatkan pecahan.
Dalam pembahasan ini, kita akan menjelajahi perbedaan antara pecahan biasa dan pecahan campuran, langkah-langkah mengubah pecahan biasa menjadi pecahan campuran, serta syarat-syarat yang harus dipenuhi agar konversi tersebut dapat dilakukan. Selain itu, kita juga akan melihat penerapan pecahan campuran dalam berbagai konteks kehidupan nyata, sehingga pemahaman konsep ini tidak hanya terbatas pada teori matematika semata.
Memahami Pecahan Biasa dan Campuran
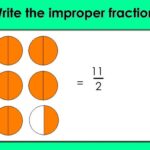
Pecahan merupakan bagian dari suatu keseluruhan. Kita mengenal dua jenis pecahan utama, yaitu pecahan biasa dan pecahan campuran. Memahami perbedaan dan kegunaan masing-masing jenis pecahan ini sangat penting dalam berbagai aplikasi matematika, mulai dari perhitungan sederhana hingga permasalahan yang lebih kompleks.
Perbedaan Pecahan Biasa dan Pecahan Campuran
Pecahan biasa ditulis dalam bentuk a/b, di mana ‘a’ adalah pembilang dan ‘b’ adalah penyebut (b ≠ 0). Pecahan biasa selalu memiliki nilai kurang dari satu. Sementara itu, pecahan campuran terdiri dari bilangan bulat dan pecahan biasa. Pecahan campuran mewakili nilai lebih dari satu.
Contoh Pecahan Biasa dan Campuran
Berikut beberapa contoh untuk mengilustrasikan perbedaan tersebut:
- Pecahan Biasa: 1/2, 3/4, 2/5
- Pecahan Campuran: 1 1/2, 2 3/4, 3 2/5
Perbandingan Pecahan Biasa dan Campuran
Tabel berikut memberikan perbandingan yang lebih rinci antara pecahan biasa dan pecahan campuran:
| Bentuk Pecahan | Pembilang | Penyebut | Contoh |
|---|---|---|---|
| Pecahan Biasa | Lebih kecil dari penyebut | Bilangan bulat positif | 1/4, 2/3, 5/8 |
| Pecahan Campuran | Bisa lebih besar atau sama dengan penyebut | Bilangan bulat positif | 1 1/2, 2 2/5, 3 7/8 |
Mengubah Pecahan Biasa Menjadi Pecahan Campuran dan Sebaliknya
Proses konversi antara pecahan biasa dan pecahan campuran melibatkan pembagian dan perkalian.
Mengubah Pecahan Biasa menjadi Pecahan Campuran: Misalnya, ubah pecahan biasa 7/3 menjadi pecahan campuran. Bagilah pembilang (7) dengan penyebut (3). Hasil bagi (2) menjadi bilangan bulat dalam pecahan campuran. Sisa bagi (1) menjadi pembilang baru, dan penyebut tetap sama (3). Jadi, 7/3 = 2 1/3.
Mengubah Pecahan Campuran menjadi Pecahan Biasa: Misalnya, ubah pecahan campuran 2 1/3 menjadi pecahan biasa. Kalikan bilangan bulat (2) dengan penyebut (3), kemudian tambahkan pembilang (1). Hasilnya (7) menjadi pembilang baru, dan penyebut tetap sama (3). Jadi, 2 1/3 = 7/3.
Situasi Penggunaan Pecahan Campuran
Pecahan campuran lebih tepat digunakan dalam situasi di mana representasi nilai yang lebih besar dari satu dibutuhkan secara intuitif. Misalnya, dalam pengukuran panjang (2 1/2 meter), berat (1 3/4 kilogram), atau jumlah barang (3 1/2 lusin). Dalam konteks ini, pecahan campuran memberikan gambaran yang lebih langsung dan mudah dipahami daripada pecahan biasa yang nilainya lebih dari satu.
Mengubah Pecahan Biasa Menjadi Pecahan Campuran: Tuliskan Bentuk Pecahan Campuran Dari Pecahan Berikut

Pecahan biasa dan pecahan campuran merupakan dua bentuk penyajian bilangan pecah yang berbeda. Pecahan biasa hanya terdiri dari pembilang dan penyebut, sedangkan pecahan campuran terdiri dari bilangan bulat dan pecahan biasa. Memahami cara mengubah pecahan biasa menjadi pecahan campuran sangat penting dalam berbagai perhitungan matematika. Proses ini melibatkan pembagian pembilang dengan penyebut untuk memperoleh bilangan bulat dan sisa pembagian yang kemudian membentuk pecahan campuran.
Langkah-Langkah Mengubah Pecahan Biasa Menjadi Pecahan Campuran
Mengubah pecahan biasa menjadi pecahan campuran merupakan proses yang sistematis dan mudah dipahami. Berikut langkah-langkahnya:
- Bagilah pembilang dengan penyebut.
- Hasil bagi merupakan bilangan bulat dalam pecahan campuran.
- Sisa pembagian menjadi pembilang baru dalam pecahan campuran.
- Penyebut tetap sama dengan penyebut pecahan biasa semula.
- Gabungkan bilangan bulat dan pecahan baru untuk membentuk pecahan campuran.
Contoh Prosedur Perubahan Pecahan Biasa Menjadi Pecahan Campuran
Berikut lima contoh prosedur perubahan pecahan biasa menjadi pecahan campuran:
- Pecahan biasa 7/3: 7 dibagi 3 hasilnya 2 sisa 1. Jadi, pecahan campurannya adalah 2 1/3.
- Pecahan biasa 11/4: 11 dibagi 4 hasilnya 2 sisa 3. Jadi, pecahan campurannya adalah 2 3/4.
- Pecahan biasa 15/7: 15 dibagi 7 hasilnya 2 sisa 1. Jadi, pecahan campurannya adalah 2 1/7.
- Pecahan biasa 23/5: 23 dibagi 5 hasilnya 4 sisa 3. Jadi, pecahan campurannya adalah 4 3/5.
- Pecahan biasa 31/8: 31 dibagi 8 hasilnya 3 sisa 7. Jadi, pecahan campurannya adalah 3 7/8.
Contoh Soal dan Penyelesaian Mengubah Pecahan Biasa Menjadi Pecahan Campuran
Berikut contoh soal dan penyelesaiannya:
Ubahlah pecahan biasa 22/6 menjadi pecahan campuran.
- Bagilah pembilang (22) dengan penyebut (6): 22 ÷ 6 = 3 sisa 4.
- Hasil bagi (3) menjadi bilangan bulat.
- Sisa pembagian (4) menjadi pembilang baru.
- Penyebut tetap 6.
- Pecahan campurannya adalah 3 4/6. Pecahan ini dapat disederhanakan menjadi 3 2/3 dengan membagi pembilang dan penyebut dengan FPB yaitu 2.
Menentukan Bagian Bulat dan Sisa dari Pecahan Biasa
Menentukan bagian bulat dan sisa dari pecahan biasa dilakukan melalui pembagian. Pembagian pembilang dengan penyebut menghasilkan hasil bagi (bagian bulat) dan sisa. Misalnya, pada pecahan 17/5, 17 dibagi 5 menghasilkan hasil bagi 3 dan sisa 2. Jadi, bagian bulat adalah 3 dan sisanya 2.
Contoh Soal dengan Tingkat Kesulitan Berbeda
Berikut contoh soal dengan tingkat kesulitan yang bervariasi:
| Tingkat Kesulitan | Soal | Penyelesaian |
|---|---|---|
| Mudah | Ubahlah 9/2 menjadi pecahan campuran. | 9 ÷ 2 = 4 sisa 1. Jadi, pecahan campurannya adalah 4 1/2. |
| Sedang | Ubahlah 25/8 menjadi pecahan campuran. | 25 ÷ 8 = 3 sisa 1. Jadi, pecahan campurannya adalah 3 1/8. |
| Sulit | Ubahlah 107/12 menjadi pecahan campuran dan sederhanakan jika perlu. | 107 ÷ 12 = 8 sisa 11. Jadi, pecahan campurannya adalah 8 11/12. (Tidak perlu disederhanakan karena FPB dari 11 dan 12 adalah 1) |
Mengenali Syarat Pecahan yang Dapat Diubah Menjadi Pecahan Campuran

Mengubah pecahan biasa menjadi pecahan campuran merupakan keterampilan dasar dalam matematika. Kemampuan ini memudahkan dalam memahami dan menghitung nilai pecahan, khususnya ketika nilai pecahan lebih besar dari satu. Pemahaman tentang syarat-syarat yang memungkinkan konversi ini sangat penting untuk menghindari kesalahan perhitungan.
Syarat utama sebuah pecahan biasa agar dapat diubah menjadi pecahan campuran adalah pembilangnya harus lebih besar daripada penyebutnya. Ini karena pecahan campuran terdiri dari bilangan bulat dan pecahan biasa, menunjukkan nilai yang lebih dari satu. Jika pembilang lebih kecil atau sama dengan penyebut, nilai pecahan kurang dari atau sama dengan satu, sehingga tidak dapat dinyatakan dalam bentuk pecahan campuran.
Contoh Pecahan yang Dapat dan Tidak Dapat Diubah Menjadi Pecahan Campuran
Berikut beberapa contoh untuk mengilustrasikan perbedaan tersebut. Pecahan 7/3 dapat diubah menjadi pecahan campuran karena pembilangnya (7) lebih besar dari penyebutnya (3). Hasilnya adalah 2 1/3. Sebaliknya, pecahan 3/7 tidak dapat diubah menjadi pecahan campuran karena pembilangnya (3) lebih kecil dari penyebutnya (7). Pecahan 3/7 tetap dalam bentuk pecahan biasa.
Penjelasan Mengapa Pecahan dengan Pembilang Lebih Kecil dari Penyebut Tidak Dapat Diubah Menjadi Pecahan Campuran, Tuliskan bentuk pecahan campuran dari pecahan berikut
Pecahan dengan pembilang lebih kecil dari penyebut merepresentasikan nilai kurang dari satu. Pecahan campuran, di sisi lain, selalu mewakili nilai lebih dari satu karena terdiri dari bagian bilangan bulat dan bagian pecahan. Oleh karena itu, konversi tidak mungkin dilakukan.
Karakteristik Pecahan Biasa yang Memungkinkan Konversi ke Pecahan Campuran
Karakteristik utama yang memungkinkan konversi adalah nilai pecahan yang lebih besar dari satu. Ini secara langsung diindikasikan oleh pembilang yang lebih besar daripada penyebut. Semakin besar selisih antara pembilang dan penyebut, semakin besar pula bagian bilangan bulat dalam pecahan campuran yang dihasilkan.
Contoh Soal Identifikasi Kemungkinan Konversi ke Pecahan Campuran
Berikut beberapa soal latihan untuk menguji pemahaman Anda:
- Tentukan apakah pecahan 12/5 dapat diubah menjadi pecahan campuran. Jelaskan alasannya.
- Tentukan apakah pecahan 4/9 dapat diubah menjadi pecahan campuran. Jelaskan alasannya.
- Tentukan apakah pecahan 25/10 dapat diubah menjadi pecahan campuran. Jelaskan alasannya.
Penerapan Pecahan Campuran dalam Kehidupan Sehari-hari
Pecahan campuran, yang menggabungkan bilangan bulat dan pecahan, merupakan representasi numerik yang sering kita temui dalam kehidupan sehari-hari. Penggunaan pecahan campuran memudahkan kita dalam memahami dan menghitung berbagai besaran, baik dalam pengukuran maupun dalam berbagai aktivitas lainnya. Kemampuan memahami dan menggunakan pecahan campuran secara efektif sangat penting untuk menyelesaikan berbagai permasalahan praktis.
Contoh Penerapan Pecahan Campuran dalam Kehidupan Sehari-hari
Pecahan campuran sering digunakan dalam berbagai situasi, memudahkan kita dalam memahami dan mengkomunikasikan ukuran dan kuantitas. Berikut beberapa contohnya:
- Memasak: Resep kue seringkali menggunakan pecahan campuran, misalnya “2 ½ cangkir tepung” atau “1 ¾ sendok teh baking powder”.
- Menjahit: Pengukuran kain untuk membuat pakaian seringkali dinyatakan dalam pecahan campuran, seperti “3 ¼ meter kain”.
- Pertukangan: Dalam proyek konstruksi atau pertukangan, ukuran kayu atau bahan bangunan lainnya seringkali dinyatakan dalam pecahan campuran, misalnya “papan kayu sepanjang 2 ⅔ meter”.
Penggunaan Pecahan Campuran dalam Pengukuran
Pecahan campuran sangat berguna dalam pengukuran panjang, berat, dan volume. Dengan menggunakan pecahan campuran, kita dapat menyatakan ukuran dengan lebih presisi dibandingkan hanya menggunakan bilangan bulat. Misalnya, tinggi badan seseorang bisa dinyatakan sebagai 175 ½ cm, berat beras 2 ¼ kg, atau volume air dalam botol 1 ¾ liter.
Contoh Soal Cerita yang Melibatkan Pecahan Campuran
Ibu membeli 3 ½ kg tepung terigu. Ia menggunakan 1 ¾ kg tepung untuk membuat kue dan sisanya untuk membuat roti. Berapa kg tepung yang digunakan Ibu untuk membuat roti?
Penyelesaian: Total tepung – tepung untuk kue = tepung untuk roti. 3 ½ kg – 1 ¾ kg = 1 ¾ kg.
Penerapan Pecahan Campuran dalam Berbagai Bidang
Berikut tabel yang menunjukkan penerapan pecahan campuran dalam berbagai bidang:
| Bidang | Contoh Penerapan | Satuan | Penjelasan |
|---|---|---|---|
| Memasak | 2 ½ cangkir gula | Cangkir | Mengukur bahan baku |
| Konstruksi | 3 ¼ meter kayu | Meter | Mengukur panjang material |
| Perdagangan | 2 ⅔ kg beras | Kilogram | Menyatakan berat barang dagangan |
| Jahit Menjahit | 1 ¾ meter kain | Meter | Mengukur kebutuhan kain |
Penyelesaian Masalah yang Melibatkan Pembagian Pecahan Campuran
Misalnya, kita memiliki 5 ½ meter kain dan ingin memotongnya menjadi potongan-potongan sepanjang 1 ¾ meter. Berapa banyak potongan yang bisa kita buat?
Penyelesaian: Kita perlu mengubah pecahan campuran menjadi pecahan biasa terlebih dahulu. 5 ½ = 11/2 dan 1 ¾ = 7/
4. Kemudian kita bagi 11/2 dengan 7/4: (11/2) / (7/4) = (11/2)
– (4/7) = 22/7 ≈ 3.14. Jadi, kita bisa membuat sekitar 3 potongan kain dengan panjang 1 ¾ meter.
Kesimpulan Akhir
Menguasai konversi antara pecahan biasa dan pecahan campuran merupakan keterampilan matematika yang sangat berguna. Kemampuan ini tidak hanya membantu dalam menyelesaikan soal-soal matematika, tetapi juga dalam memecahkan masalah di kehidupan sehari-hari yang melibatkan pengukuran, pembagian, dan berbagai perhitungan lainnya. Dengan memahami konsep ini secara mendalam, kita dapat dengan lebih mudah mengaplikasikannya dalam berbagai situasi dan menyelesaikan permasalahan yang berkaitan dengan pecahan.