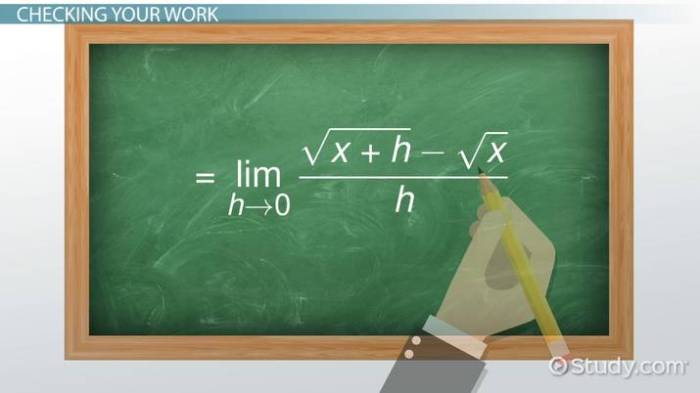Turunan akar x merupakan konsep penting dalam kalkulus yang menjelaskan laju perubahan fungsi akar kuadrat. Memahami turunan akar x membuka pintu untuk menyelesaikan berbagai permasalahan, mulai dari optimasi fungsi hingga analisis grafik. Konsep limit dan aturan rantai memainkan peran krusial dalam mencari turunan ini, dan pemahaman yang mendalam akan memungkinkan Anda untuk mengaplikasikannya dalam berbagai bidang, termasuk fisika, teknik, dan ekonomi.
Dari definisi matematis hingga penerapan praktis, bahasan ini akan menguraikan langkah-langkah mencari turunan akar x, membandingkannya dengan turunan fungsi pangkat lainnya, dan menunjukkan penerapannya dalam berbagai konteks. Dengan contoh soal dan ilustrasi grafik, pemahaman Anda tentang turunan akar x akan semakin komprehensif.
Pengertian Turunan Akar x
Turunan merupakan konsep fundamental dalam kalkulus yang menjelaskan laju perubahan suatu fungsi. Mencari turunan fungsi yang melibatkan akar x, atau secara matematis ditulis sebagai √x atau x 1/2, memerlukan pemahaman tentang aturan diferensiasi dan terkadang aturan rantai. Artikel ini akan membahas secara detail bagaimana kita dapat menentukan turunan dari fungsi-fungsi yang mengandung akar x.
Definisi Matematis Turunan Akar x
Secara matematis, turunan dari akar x (f(x) = √x = x 1/2) dapat ditentukan menggunakan definisi turunan sebagai limit:
f'(x) = limΔx→0 [(√(x + Δx)
√x) / Δx]
Dengan menggunakan manipulasi aljabar dan sifat limit, kita dapat menyederhanakan ekspresi di atas menjadi:
f'(x) = 1 / (2√x)
Rumus ini menunjukkan bahwa turunan dari akar x adalah 1 dibagi dua kali akar x. Perlu diingat bahwa x harus bernilai positif karena akar kuadrat dari bilangan negatif tidak terdefinisi dalam bilangan real.
Contoh Fungsi yang Melibatkan Akar x dan Turunannya
Berikut beberapa contoh fungsi yang melibatkan akar x dan turunannya:
- f(x) = 3√x; f'(x) = 3/(2√x)
- f(x) = x 2√x; f'(x) = (5x 3/2)/2
- f(x) = √(x + 2); f'(x) = 1/(2√(x+2))
Contoh-contoh ini menunjukkan bagaimana turunan dari fungsi yang melibatkan akar x dapat dihitung dengan menerapkan aturan diferensiasi dasar dan aturan rantai, jika diperlukan.
Konsep Limit dalam Mencari Turunan Akar x
Konsep limit sangat krusial dalam menentukan turunan. Seperti yang ditunjukkan pada definisi matematis di atas, turunan akar x ditemukan dengan menghitung limit dari suatu ekspresi ketika Δx mendekati nol. Limit ini merepresentasikan laju perubahan sesaat fungsi pada titik x tertentu. Tanpa pemahaman limit, kita tidak dapat mendefinisikan secara tepat apa itu turunan.
Penggunaan Aturan Rantai dalam Mencari Turunan Fungsi yang Mengandung Akar x
Aturan rantai digunakan ketika kita mencari turunan dari fungsi komposit, yaitu fungsi yang terdiri dari fungsi lain di dalamnya. Jika fungsi yang mengandung akar x merupakan fungsi komposit, maka aturan rantai harus diterapkan. Aturan rantai menyatakan bahwa turunan dari fungsi komposit f(g(x)) adalah f'(g(x))
– g'(x).
Contoh Soal dan Penyelesaiannya yang Melibatkan Turunan Akar x dan Aturan Rantai
Misalkan kita memiliki fungsi f(x) = √(x² + 1). Untuk mencari turunannya, kita perlu menggunakan aturan rantai. Fungsi ini dapat dianggap sebagai komposisi dari dua fungsi: g(x) = x² + 1 dan h(u) = √u. Maka:
- Turunan dari h(u) terhadap u adalah h'(u) = 1/(2√u).
- Turunan dari g(x) terhadap x adalah g'(x) = 2x.
- Dengan aturan rantai, turunan dari f(x) adalah f'(x) = h'(g(x))
- g'(x) = [1/(2√(x² + 1))]
- 2x = x/√(x² + 1).
Jadi, turunan dari f(x) = √(x² + 1) adalah x/√(x² + 1).
Mencari Turunan Akar x
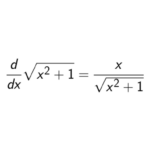
Mencari turunan fungsi merupakan konsep fundamental dalam kalkulus. Pemahaman tentang turunan akar x, khususnya, sangat penting karena akar kuadrat sering muncul dalam berbagai aplikasi, mulai dari fisika hingga ekonomi. Bagian ini akan menjelaskan secara detail bagaimana mencari turunan fungsi akar x dan aplikasinya.
Langkah-langkah Mencari Turunan f(x) = √x
Untuk mencari turunan dari fungsi f(x) = √x, kita dapat menggunakan aturan pangkat dan sifat-sifat turunan. Pertama, kita tulis ulang fungsi tersebut dalam bentuk pangkat: f(x) = x 1/2. Kemudian, kita terapkan aturan pangkat untuk turunan: d/dx (x n) = nx n-1.
Dengan demikian, turunan dari f(x) = x 1/2 adalah:
f'(x) = (1/2)x(1/2)-1 = (1/2)x -1/2 = 1/(2√x)
Jadi, turunan dari √x adalah 1/(2√x).
Perbandingan Turunan Fungsi Pangkat
Berikut tabel perbandingan turunan beberapa fungsi pangkat, termasuk akar x:
| Fungsi | Turunan | Contoh Soal | Penyelesaian |
|---|---|---|---|
| f(x) = x² | f'(x) = 2x | Cari turunan dari f(x) = 3x² | f'(x) = 6x |
| f(x) = x³ | f'(x) = 3x² | Cari turunan dari f(x) = x³ + 2x | f'(x) = 3x² + 2 |
| f(x) = √x = x1/2 | f'(x) = 1/(2√x) | Cari turunan dari f(x) = 2√x | f'(x) = 1/√x |
| f(x) = 1/x = x-1 | f'(x) = -1/x² | Cari turunan dari f(x) = 5/x | f'(x) = -5/x² |
Mencari Turunan Fungsi Kompleks yang Melibatkan Akar x, Turunan akar x
Mencari turunan fungsi yang lebih kompleks yang melibatkan akar x seringkali memerlukan penerapan aturan rantai. Sebagai contoh, mari kita cari turunan dari f(x) = x²√x.
Pertama, kita tulis ulang fungsi sebagai f(x) = x²
– x 1/2 = x 5/2. Kemudian, kita terapkan aturan pangkat:
f'(x) = (5/2)x(5/2)-1 = (5/2)x 3/2 = (5/2)x√x
Algoritma Mencari Turunan Akar x
Algoritma berikut dapat digunakan untuk mencari turunan akar x dalam program komputer. Algoritma ini mengasumsikan input berupa fungsi dalam bentuk pangkat.
- Tentukan fungsi f(x) dalam bentuk pangkat (misalnya, xn).
- Ekstrak nilai n (pangkat).
- Hitung turunan menggunakan rumus: f'(x) = n
x(n-1).
- Kembalikan nilai f'(x).
Penerapan Turunan Akar x dalam Geometri
Turunan akar x dapat digunakan untuk menyelesaikan berbagai masalah geometri. Misalnya, dalam mencari laju perubahan luas lingkaran terhadap perubahan jari-jarinya. Jika luas lingkaran A = πr², maka turunannya terhadap r (jari-jari) adalah dA/dr = 2πr. Jika jari-jari dinyatakan sebagai fungsi waktu, misalnya r(t) = √t, maka laju perubahan luas terhadap waktu dapat ditemukan dengan menggunakan aturan rantai.
Penerapan Turunan Akar x
Turunan akar x, atau secara matematis ditulis sebagai d/dx(√x), memiliki aplikasi yang luas di berbagai bidang, dari optimasi fungsi hingga analisis grafik. Pemahaman tentang turunan ini sangat krusial dalam menyelesaikan berbagai permasalahan matematika dan sains yang melibatkan fungsi akar kuadrat.
Optimasi Fungsi dengan Turunan Akar x
Dalam optimasi, turunan akar x digunakan untuk menemukan nilai maksimum atau minimum suatu fungsi yang mengandung akar kuadrat. Dengan mencari titik kritis (di mana turunannya sama dengan nol atau tak terdefinisi), kita dapat menentukan titik-titik ekstrem fungsi tersebut. Proses ini sangat berguna dalam berbagai permasalahan, seperti menentukan dimensi optimal suatu wadah untuk memaksimalkan volume dengan luas permukaan tertentu.
Penerapan Turunan Akar x dalam Fisika dan Ilmu Teknik
Turunan akar x sering muncul dalam persamaan fisika dan teknik yang menggambarkan fenomena alam atau sistem rekayasa. Misalnya, dalam mekanika klasik, perhitungan kecepatan atau percepatan partikel yang bergerak sepanjang lintasan yang didefinisikan oleh fungsi akar kuadrat akan melibatkan turunan akar x. Contoh lainnya adalah dalam analisis tegangan pada material, dimana rumus-rumus tertentu dapat mengandung akar kuadrat yang membutuhkan turunan untuk analisis lebih lanjut.
Analisis Grafik Fungsi dengan Turunan Akar x
Turunan akar x berperan penting dalam analisis grafik fungsi. Dengan menghitung turunan pertama, kita dapat menentukan interval di mana fungsi tersebut naik atau turun. Turunan kedua membantu menentukan kecekungan grafik (cekung ke atas atau ke bawah), dan titik belok. Informasi ini memungkinkan kita untuk membuat sketsa grafik fungsi dengan akurat dan memahami perilaku fungsi tersebut.
Contoh Kasus Ekonomi yang Menggunakan Turunan Akar x
Dalam ekonomi, fungsi produksi Cobb-Douglas, yang sering digunakan untuk memodelkan hubungan antara input dan output, terkadang melibatkan akar kuadrat. Misalnya, fungsi produksi Q = K 1/2L 1/2 (dimana Q adalah output, K adalah modal, dan L adalah tenaga kerja) membutuhkan turunan akar x untuk menentukan produktivitas marginal modal atau tenaga kerja. Dengan demikian, turunan akar x membantu dalam analisis efisiensi alokasi sumber daya.
Pemahaman mendalam tentang turunan akar x merupakan kunci penting dalam penguasaan kalkulus. Kemampuan untuk menghitung dan menginterpretasikan turunan ini membuka jalan bagi pemahaman yang lebih komprehensif terhadap berbagai konsep dan penerapannya di berbagai disiplin ilmu.
Grafik Fungsi dan Turunannya

Memahami grafik fungsi akar x dan turunannya sangat penting untuk menganalisis perilaku fungsi tersebut. Dengan mengamati grafik, kita dapat dengan mudah mengidentifikasi titik kritis, kemiringan, serta bagaimana perubahan konstanta memengaruhi bentuk kurva. Berikut ini pembahasan lebih lanjut mengenai grafik fungsi akar x dan turunannya.
Grafik Fungsi f(x) = √x dan Turunannya f'(x)
Grafik fungsi f(x) = √x merupakan setengah parabola yang terletak di kuadran I, dimulai dari titik (0,0) dan terus meningkat secara perlahan. Kurva ini selalu naik (monotonik naik) untuk x ≥ 0. Turunannya, f'(x) = 1/(2√x), menunjukkan kemiringan garis singgung pada setiap titik. Perhatikan bahwa kemiringan garis singgung mendekati tak hingga saat x mendekati 0 dan semakin kecil seiring bertambahnya nilai x.
Titik kritis hanya terdapat di x = 0, dimana fungsi memiliki nilai minimum 0. Untuk x > 0, fungsi selalu naik dengan kemiringan yang terus menurun.
Grafik Fungsi f(x) = √x + 2 dan f(x) = 2√x
Grafik f(x) = √x + 2 merupakan pergeseran vertikal dari grafik f(x) = √x sebesar 2 satuan ke atas. Titik potong sumbu y menjadi (0,2), sementara titik potong sumbu x tetap di (0,0). Grafik f(x) = 2√x merupakan perbesaran vertikal dari grafik f(x) = √x dengan faktor skala 2. Kurva ini lebih curam dibandingkan f(x) = √x dan titik potong sumbu x tetap di (0,0), sedangkan titik potong sumbu y tetap di (0,0).
Pengaruh Perubahan Konstanta pada Fungsi Akar x
Perubahan konstanta pada fungsi akar x akan memengaruhi bentuk grafik dan turunannya. Konstanta yang ditambahkan atau dikurangkan akan mengakibatkan pergeseran vertikal grafik. Konstanta yang dikalikan akan mengakibatkan perbesaran atau pengecilan vertikal. Sebagai contoh, f(x) = a√x + b, dimana ‘a’ menentukan skala vertikal dan ‘b’ menentukan pergeseran vertikal. Perubahan ‘a’ dan ‘b’ akan memengaruhi kemiringan garis singgung pada setiap titik, yang tercermin dalam turunannya.
Perbandingan Grafik f(x) = √x dan g(x) = x^(1/3)
Grafik f(x) = √x dan g(x) = x^(1/3) memiliki perbedaan yang signifikan. f(x) = √x hanya terdefinisi untuk x ≥ 0 dan selalu naik. g(x) = x^(1/3) terdefinisi untuk semua x dan memiliki kemiringan tak hingga di x = 0. Turunan f'(x) = 1/(2√x) mendekati tak hingga saat x mendekati 0, sedangkan turunan g'(x) = (1/3)x^(-2/3) juga mendekati tak hingga saat x mendekati 0.
Namun, g(x) memiliki kemiringan yang lebih curam di sekitar x = 0 dibandingkan f(x).
Hubungan Grafik Fungsi dan Grafik Turunannya
Grafik turunan suatu fungsi menunjukkan kemiringan garis singgung pada setiap titik grafik fungsi tersebut. Jika grafik fungsi naik, maka grafik turunannya bernilai positif. Jika grafik fungsi turun, maka grafik turunannya bernilai negatif. Untuk fungsi f(x) = √x, grafik fungsi selalu naik, dan grafik turunannya selalu positif, namun nilainya terus menurun seiring bertambahnya x. Hubungan ini menunjukkan bagaimana perubahan kemiringan grafik fungsi tercermin dalam nilai turunannya.
Ringkasan Penutup

Menguasai turunan akar x bukan hanya tentang memahami rumus, tetapi juga tentang memahami implikasinya dalam berbagai aplikasi. Kemampuan untuk menganalisis laju perubahan fungsi akar kuadrat memberikan alat yang ampuh untuk memecahkan masalah di berbagai disiplin ilmu. Dengan pemahaman yang kuat tentang konsep ini, Anda akan mampu menangani permasalahan yang lebih kompleks dan mengaplikasikannya secara efektif dalam berbagai konteks.