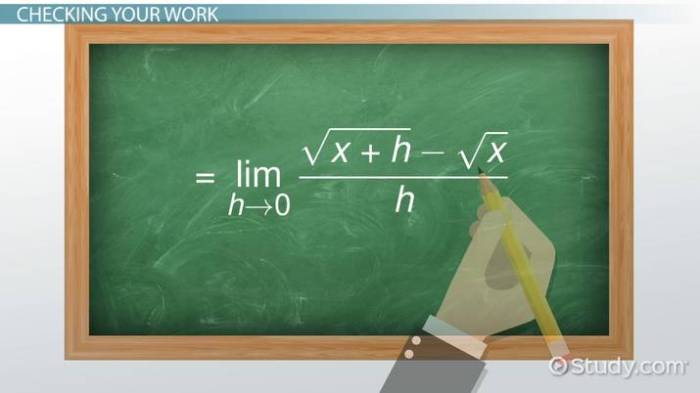
Turunan pertama, kunci untuk menguak misteri perubahan. Konsep matematika fundamental ini tak hanya sekadar rumus dan angka, melainkan jendela untuk memahami bagaimana suatu besaran berubah seiring waktu atau variabel lainnya. Dari menentukan kecepatan dan percepatan benda bergerak hingga memaksimalkan keuntungan perusahaan, turunan pertama menjadi alat analisis yang ampuh dalam berbagai bidang.
Artikel ini akan mengupas tuntas konsep turunan pertama, mulai dari definisi matematis hingga penerapannya dalam berbagai konteks. Kita akan menjelajahi cara mencari turunan pertama berbagai jenis fungsi, menganalisis grafik fungsi berdasarkan turunannya, dan melihat bagaimana turunan pertama membantu menyelesaikan masalah optimasi dan analisis perubahan.
Pengertian Turunan Pertama
Turunan pertama, dalam kalkulus, merupakan konsep fundamental yang menggambarkan laju perubahan sesaat suatu fungsi. Pemahamannya krusial dalam berbagai bidang, mulai dari fisika dan teknik hingga ekonomi dan ilmu komputer. Konsep ini memberikan alat yang ampuh untuk menganalisis perilaku fungsi dan menemukan titik-titik kritisnya.
Definisi Matematis Turunan Pertama
Secara matematis, turunan pertama dari suatu fungsi f(x) di titik x didefinisikan sebagai limit dari perubahan fungsi terhadap perubahan x ketika perubahan x mendekati nol. Hal ini dapat dituliskan sebagai:
f'(x) = limΔx→0 [f(x + Δx)
f(x)] / Δx
Jika limit ini ada, maka fungsi f(x) dikatakan terdiferensialkan di titik x, dan f'(x) adalah turunan pertamanya.
Contoh Fungsi dan Turunan Pertamanya
Sebagai contoh, perhatikan fungsi kuadrat f(x) = x² + 2x + 1. Turunan pertamanya dapat dihitung menggunakan aturan pangkat, yaitu menurunkan pangkat dan mengalikannya dengan koefisien. Hasilnya adalah f'(x) = 2x + 2. Artinya, laju perubahan fungsi f(x) pada titik x manapun diberikan oleh 2x + 2.
Contoh lain, fungsi eksponensial f(x) = ex memiliki turunan pertama yang sama dengan dirinya sendiri, yaitu f'(x) = ex.
Interpretasi Geometri Turunan Pertama
Secara geometri, turunan pertama dari suatu fungsi pada suatu titik mewakili gradien (kemiringan) garis singgung kurva fungsi tersebut pada titik yang sama. Gradien ini menunjukkan seberapa cepat fungsi tersebut berubah pada titik tersebut. Semakin besar nilai mutlak gradien, semakin curam kemiringan garis singgung, dan semakin cepat perubahan fungsi.
Bayangkan sebuah kurva fungsi. Garis singgung pada suatu titik akan memiliki kemiringan yang sama dengan nilai turunan pertama fungsi pada titik tersebut. Jika turunan pertama positif, garis singgung naik; jika negatif, garis singgung turun; dan jika nol, garis singgung horizontal (menunjukkan titik stasioner).
Penerapan Turunan Pertama dalam Berbagai Bidang
Konsep turunan pertama memiliki aplikasi yang luas. Dalam fisika, misalnya, turunan pertama posisi terhadap waktu memberikan kecepatan, dan turunan pertama kecepatan terhadap waktu memberikan percepatan. Dalam ekonomi, turunan pertama fungsi biaya atau keuntungan digunakan untuk menentukan titik maksimum atau minimum, yang penting dalam pengambilan keputusan bisnis. Dalam ilmu komputer, turunan pertama digunakan dalam algoritma optimasi dan pembelajaran mesin.
Perbandingan Turunan Pertama Fungsi Aljabar dan Trigonometri
Berikut tabel perbandingan turunan pertama fungsi aljabar dan fungsi trigonometri:
| Jenis Fungsi | Fungsi Awal | Turunan Pertama | Contoh |
|---|---|---|---|
| Fungsi Aljabar (Pangkat) | f(x) = xn | f'(x) = nxn-1 | f(x) = x³, f'(x) = 3x² |
| Fungsi Aljabar (Linear) | f(x) = ax + b | f'(x) = a | f(x) = 2x + 5, f'(x) = 2 |
| Fungsi Trigonometri (sin x) | f(x) = sin x | f'(x) = cos x | f(x) = sin x, f'(x) = cos x |
| Fungsi Trigonometri (cos x) | f(x) = cos x | f'(x) = -sin x | f(x) = cos x, f'(x) = -sin x |
Mencari Turunan Pertama
Turunan pertama merupakan konsep fundamental dalam kalkulus yang menggambarkan laju perubahan suatu fungsi. Memahami cara mencari turunan pertama sangat krusial dalam berbagai aplikasi, mulai dari optimasi hingga analisis pergerakan. Berikut ini akan diuraikan langkah-langkah mencari turunan pertama untuk beberapa jenis fungsi.
Turunan Pertama Fungsi Polinomial
Fungsi polinomial merupakan fungsi yang terdiri dari suku-suku dengan pangkat bilangan bulat non-negatif. Mencari turunan pertama fungsi polinomial relatif mudah. Aturan dasarnya adalah menurunkan pangkat setiap suku dengan satu, lalu mengalikan koefisien dengan pangkat awal. Konstanta akan menjadi nol setelah diturunkan.
- Misalnya, jika f(x) = 3x² + 2x + 5, maka turunan pertamanya, f'(x) = 6x + 2. Perhatikan bahwa suku konstanta 5 menjadi 0 setelah diturunkan.
- Sebagai contoh lain, jika g(x) = x³
-4x² + 7x – 1, maka turunan pertamanya, g'(x) = 3x²
-8x + 7.
Penerapan Aturan Rantai pada Fungsi Komposit
Aturan rantai digunakan untuk mencari turunan fungsi komposit, yaitu fungsi yang tersusun dari fungsi-fungsi lain. Aturan rantai menyatakan bahwa turunan dari fungsi komposit adalah perkalian turunan fungsi luar terhadap fungsi dalam, dikalikan dengan turunan fungsi dalam.
Secara matematis, jika y = f(g(x)), maka dy/dx = f'(g(x))
– g'(x).
- Contoh: Misalkan h(x) = (2x + 1)³. Di sini, fungsi luarnya adalah f(u) = u³ dan fungsi dalamnya adalah g(x) = 2x + 1. Maka, h'(x) = 3(2x + 1)²
– 2 = 6(2x + 1)².
Turunan Pertama Fungsi Implisit
Fungsi implisit adalah fungsi yang tidak dinyatakan secara eksplisit dalam bentuk y = f(x). Untuk mencari turunan pertamanya, kita perlu menggunakan teknik diferensiasi implisit, yaitu mendiferensialkan kedua ruas persamaan terhadap x, kemudian menyelesaikan persamaan tersebut untuk dy/dx.
- Contoh: Perhatikan persamaan x² + y² = 25. Diferensiasi implisit terhadap x menghasilkan 2x + 2y(dy/dx) = 0. Dengan menyelesaikan persamaan ini untuk dy/dx, kita peroleh dy/dx = -x/y.
Turunan Pertama Fungsi Trigonometri
Mencari turunan fungsi trigonometri melibatkan penggunaan rumus-rumus turunan standar untuk fungsi sinus, kosinus, dan tangen. Rumus-rumus ini perlu dihafal dan dipahami.
- Turunan dari sin(x) adalah cos(x).
- Turunan dari cos(x) adalah -sin(x).
- Turunan dari tan(x) adalah sec²(x).
- Contoh: Jika f(x) = sin(2x), maka f'(x) = 2cos(2x) (menggunakan aturan rantai).
Turunan Pertama Fungsi Eksponen dan Logaritma
Fungsi eksponen dan logaritma memiliki aturan turunan yang spesifik. Rumus-rumus ini juga perlu dipahami dan dihafal.
Berikut contoh soal dan penyelesaiannya:
| Soal | Penyelesaian |
|---|---|
| Tentukan turunan pertama dari f(x) = e2x | f'(x) = 2e2x |
| Tentukan turunan pertama dari g(x) = ln(x²) | g'(x) = 2/x |
Penerapan Turunan Pertama

Turunan pertama, sebagai konsep inti dalam kalkulus, memiliki penerapan yang luas dan mendalam dalam berbagai bidang, mulai dari matematika murni hingga ilmu terapan seperti fisika dan ekonomi. Pemahaman yang kuat tentang turunan pertama memungkinkan kita untuk menganalisis perilaku fungsi, mengoptimalkan proses, dan memecahkan berbagai masalah yang melibatkan perubahan dan laju perubahan.
Menentukan Titik Stasioner Suatu Fungsi
Titik stasioner merupakan titik pada grafik fungsi di mana turunan pertama fungsi tersebut bernilai nol (f'(x) = 0) atau tidak terdefinisi. Titik-titik ini menandai perubahan arah kemiringan kurva. Dengan menemukan titik-titik stasioner, kita dapat mengidentifikasi potensi titik maksimum, minimum, atau titik belok.
Menentukan Nilai Maksimum dan Minimum Suatu Fungsi, Turunan pertama
Setelah titik stasioner ditemukan, turunan pertama dapat digunakan untuk menentukan apakah titik tersebut merupakan maksimum lokal, minimum lokal, atau titik belok. Uji turunan kedua (f”(x)) atau uji turunan pertama pada interval sekitar titik stasioner dapat digunakan untuk mengklasifikasikan jenis titik stasioner tersebut. Nilai maksimum dan minimum sangat penting dalam berbagai masalah optimasi, seperti menentukan ukuran kemasan yang paling efisien atau menentukan harga jual yang memaksimalkan keuntungan.
Contoh Kasus Penerapan Turunan Pertama dalam Menyelesaikan Masalah Optimasi
Misalnya, sebuah perusahaan ingin mendesain kaleng silinder dengan volume tertentu agar biaya bahan baku seminimal mungkin. Dengan menggunakan rumus volume dan luas permukaan silinder, kita dapat membentuk fungsi yang merepresentasikan biaya bahan baku sebagai fungsi dari jari-jari dan tinggi silinder. Dengan mencari turunan pertama fungsi biaya dan menyamakannya dengan nol, kita dapat menemukan jari-jari dan tinggi silinder yang meminimalkan biaya bahan baku.
Proses ini melibatkan penggunaan turunan pertama untuk menemukan titik minimum fungsi biaya.
Menentukan Interval Fungsi Naik dan Turun
Turunan pertama juga memberikan informasi tentang interval di mana fungsi naik atau turun. Jika f'(x) > 0 pada suatu interval, maka fungsi naik pada interval tersebut. Sebaliknya, jika f'(x) < 0, maka fungsi turun pada interval tersebut. Informasi ini berguna untuk memahami perilaku keseluruhan fungsi dan menggambar grafiknya dengan akurat.
Dalam fisika, turunan pertama dari fungsi posisi terhadap waktu memberikan kecepatan, sementara turunan pertama dari fungsi kecepatan terhadap waktu memberikan percepatan. Analisis ini memungkinkan kita untuk memahami dinamika gerak suatu objek, misalnya menentukan kecepatan maksimum atau waktu yang dibutuhkan untuk mencapai suatu kecepatan tertentu.
Turunan Pertama dan Grafik Fungsi
Turunan pertama suatu fungsi memiliki peran krusial dalam memahami perilaku grafik fungsi tersebut. Ia memberikan informasi tentang kemiringan garis singgung di setiap titik pada kurva, mengungkapkan tingkat perubahan fungsi dan membantu mengidentifikasi karakteristik penting seperti titik stasioner, titik belok, serta konveksitas dan konkavitas grafik.
Kemiringan Garis Singgung dan Perubahan Nilai x
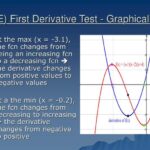
Perhatikan grafik fungsi kuadrat, misalnya f(x) = x². Turunan pertamanya adalah f'(x) = 2x. Nilai f'(x) pada suatu titik x mewakili kemiringan garis singgung kurva di titik tersebut. Jika x bernilai positif, f'(x) juga positif, menunjukkan garis singgung memiliki kemiringan positif (naik dari kiri ke kanan). Sebaliknya, jika x negatif, f'(x) negatif, dan garis singgung memiliki kemiringan negatif (turun dari kiri ke kanan).
Semakin besar nilai absolut x, semakin curam kemiringan garis singgungnya. Pada titik x = 0, f'(x) = 0, menunjukkan garis singgung horizontal, yang merupakan titik stasioner (dalam kasus ini, titik minimum).
Ilustrasi: Bayangkan sebuah bola menggelinding di sepanjang kurva parabola. Kecepatan bola pada setiap titik sebanding dengan kemiringan garis singgung di titik tersebut. Kecepatan bola akan meningkat seiring dengan bertambahnya nilai x positif, dan menurun seiring dengan bertambahnya nilai x negatif.
Identifikasi Titik Belok
Titik belok adalah titik di mana kurva berubah dari cekung ke cembung atau sebaliknya. Pada titik belok, turunan kedua fungsi, f”(x), sama dengan nol atau tidak terdefinisi. Dengan menganalisis turunan pertama, kita dapat menemukan kandidat titik belok. Setelah menemukan titik-titik tersebut, kita perlu memeriksa tanda turunan kedua di sekitar titik tersebut untuk memastikan perubahan konkavitas.
Contoh: Fungsi f(x) = x³ memiliki turunan pertama f'(x) = 3x² dan turunan kedua f”(x) = 6x. f”(x) = 0 ketika x = 0. Pemeriksaan tanda f”(x) di sekitar x = 0 menunjukkan perubahan konkavitas, sehingga x = 0 adalah titik belok.
Hubungan Turunan Pertama dan Konkavitas/Konveksitas
Konkavitasi dan konveksitas grafik fungsi berhubungan erat dengan turunan pertama dan kedua. Jika turunan pertama fungsi meningkat ( f'(x) naik), maka grafik fungsi bersifat konveks (cekung ke atas). Sebaliknya, jika turunan pertama fungsi menurun ( f'(x) turun), maka grafik fungsi bersifat konkav (cekung ke bawah). Turunan kedua memberikan informasi yang lebih pasti tentang konkavitas/konveksitas.
Sebagai contoh, fungsi eksponensial f(x) = ex selalu memiliki turunan pertama positif dan meningkat, sehingga grafiknya selalu konveks.
Langkah-langkah Membuat Sketsa Grafik Fungsi Berdasarkan Turunan Pertama
- Tentukan domain dan range fungsi.
- Cari titik potong sumbu x dan y.
- Temukan turunan pertama fungsi, f'(x).
- Tentukan titik-titik kritis (di mana f'(x) = 0 atau f'(x) tidak terdefinisi).
- Analisis tanda f'(x) di sekitar titik kritis untuk menentukan interval di mana fungsi naik atau turun.
- Cari turunan kedua, f”(x) (opsional, untuk menentukan titik belok dan konkavitas/konveksitas).
- Gambarkan sketsa grafik berdasarkan informasi yang telah diperoleh.
Penentuan Titik Potong Sumbu x dan y
Titik potong sumbu x diperoleh dengan menyelesaikan persamaan f(x) = 0. Titik potong sumbu y diperoleh dengan menghitung nilai f(0). Turunan pertama tidak secara langsung digunakan untuk menentukan titik potong sumbu x dan y, namun informasi tentang perilaku fungsi (naik/turun) yang didapat dari turunan pertama membantu dalam menentukan interval yang mungkin mengandung titik potong sumbu x.
Misalnya, untuk fungsi f(x) = x²
-4 , titik potong sumbu x diperoleh dengan menyelesaikan x²
-4 = 0 , menghasilkan x = ±2. Titik potong sumbu y adalah f(0) = -4.
Kesimpulan Akhir: Turunan Pertama
Menguasai turunan pertama membuka pintu menuju pemahaman yang lebih dalam tentang perubahan dan optimasi. Dari dunia fisika hingga ekonomi, kemampuan menganalisis perubahan menjadi kunci dalam pengambilan keputusan dan inovasi. Dengan pemahaman yang mendalam tentang turunan pertama, kita mampu memodelkan dan memprediksi fenomena kompleks, membuka jalan bagi penemuan dan kemajuan baru.



