Uji Statistik Panduan Lengkap Analisis Data

Uji statistik merupakan alat penting dalam penelitian untuk menganalisis data dan menarik kesimpulan yang bermakna. Memahami berbagai jenis uji statistik, mulai dari uji t hingga uji chi-square, sangat krusial untuk memastikan hasil penelitian akurat dan dapat diandalkan. Panduan ini akan mengupas tuntas berbagai metode uji statistik, langkah-langkah penerapannya, serta interpretasi hasil yang tepat, sehingga pembaca dapat mengaplikasikannya dalam penelitian mereka sendiri.

Dari memahami perbedaan antara uji parametrik dan non-parametrik hingga memilih uji statistik yang sesuai dengan jenis data, panduan ini akan memberikan pemahaman yang komprehensif. Kita akan membahas langkah-langkah melakukan uji statistik, mulai dari perumusan hipotesis hingga interpretasi nilai p-value, dilengkapi dengan contoh kasus dan ilustrasi yang mudah dipahami. Dengan demikian, pembaca dapat meningkatkan kemampuan analisis data mereka dan menghasilkan temuan penelitian yang lebih berkualitas.

Pengantar Uji Statistik

Uji statistik merupakan alat penting dalam penelitian untuk menganalisis data dan menarik kesimpulan yang valid. Penggunaan uji statistik yang tepat sangat krusial untuk memastikan hasil penelitian akurat dan dapat diandalkan. Pemahaman tentang berbagai jenis uji statistik dan kapan menggunakannya merupakan kunci keberhasilan dalam menafsirkan data secara tepat.

Jenis-jenis Uji Statistik

Berbagai jenis uji statistik tersedia, masing-masing dirancang untuk menjawab pertanyaan penelitian yang spesifik dan sesuai dengan jenis data yang dikumpulkan. Pemilihan uji statistik yang tepat bergantung pada beberapa faktor, termasuk jenis data (skala nominal, ordinal, interval, atau rasio), distribusi data, dan tujuan analisis.

• Uji t: Digunakan untuk membandingkan rata-rata dua kelompok. Contoh: Membandingkan rata-rata tinggi badan siswa laki-laki dan perempuan.
• ANOVA (Analysis of Variance): Digunakan untuk membandingkan rata-rata lebih dari dua kelompok. Contoh: Membandingkan hasil panen dari tiga jenis pupuk yang berbeda.
• Uji Chi-Square: Digunakan untuk menganalisis hubungan antara dua variabel kategorik. Contoh: Menganalisis hubungan antara jenis kelamin dan preferensi warna.
• Uji Korelasi: Digunakan untuk mengukur kekuatan dan arah hubungan antara dua variabel numerik. Contoh: Menganalisis hubungan antara tinggi badan dan berat badan.
• Uji Regresi: Digunakan untuk memprediksi nilai variabel dependen berdasarkan nilai variabel independen. Contoh: Memprediksi nilai ujian siswa berdasarkan jumlah jam belajar.

Tabel Perbandingan Uji Statistik

|+ Jenis Uji Statistik|-| Jenis Data | Tujuan Analisis | Asumsi ||-| Uji t | Interval/Rasio | Membandingkan rata-rata dua kelompok | Data terdistribusi normal, varians sama ||-| ANOVA | Interval/Rasio | Membandingkan rata-rata lebih dari dua kelompok | Data terdistribusi normal, varians sama ||-| Uji Chi-Square | Nominal/Ordinal | Menganalisis hubungan antara dua variabel kategorik | Ukuran sampel cukup besar ||-| Uji Korelasi (Pearson) | Interval/Rasio | Mengukur hubungan linear antara dua variabel | Data terdistribusi normal, hubungan linear ||-| Uji Regresi Linear | Interval/Rasio | Memprediksi nilai variabel dependen berdasarkan variabel independen | Data terdistribusi normal, hubungan linear |

Perbedaan Uji Parametrik dan Non-parametrik

Uji statistik dibagi menjadi dua kategori utama: parametrik dan non-parametrik. Perbedaan utama terletak pada asumsi yang mendasari masing-masing jenis uji.

Ilustrasi Perbedaan Uji Parametrik dan Non-parametrik

Uji parametrik, seperti uji t dan ANOVA, mengasumsikan data terdistribusi normal dan memiliki varians yang sama antar kelompok. Jika asumsi ini terpenuhi, uji parametrik memiliki kekuatan statistik yang lebih besar. Sebagai contoh, jika kita ingin membandingkan rata-rata pendapatan dua kelompok penduduk, dan data pendapatan terdistribusi normal, maka uji t merupakan pilihan yang tepat. Namun, jika data tidak terdistribusi normal atau variansnya tidak sama, maka hasil uji parametrik dapat bias.

Sebaliknya, uji non-parametrik, seperti uji Mann-Whitney U dan uji Kruskal-Wallis, tidak memerlukan asumsi distribusi data normal. Uji ini lebih fleksibel dan dapat digunakan pada data yang tidak memenuhi asumsi uji parametrik. Misalnya, jika kita ingin membandingkan peringkat kepuasan pelanggan terhadap dua produk berbeda, dan data peringkat tidak terdistribusi normal, maka uji Mann-Whitney U lebih sesuai digunakan.

Prosedur Melakukan Uji Statistik

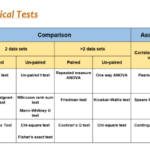
Uji statistik merupakan alat penting dalam penelitian untuk menganalisis data dan menarik kesimpulan yang bermakna. Prosedur yang sistematis sangat krusial untuk memastikan hasil yang akurat dan interpretasi yang tepat. Langkah-langkah umum dalam melakukan uji statistik akan diuraikan berikut ini, disertai contoh penerapan uji t-test dan penjelasan perhitungan nilai p-value.

Langkah-Langkah Umum dalam Uji Statistik

Secara umum, melakukan uji statistik melibatkan beberapa tahapan penting. Tahapan ini memastikan analisis data dilakukan secara sistematis dan hasilnya dapat diinterpretasi dengan tepat.

1. Perumusan Hipotesis: Menentukan hipotesis nol (H0) dan hipotesis alternatif (H1). Hipotesis nol menyatakan tidak ada perbedaan atau hubungan, sedangkan hipotesis alternatif menyatakan adanya perbedaan atau hubungan.
2. Pemilihan Uji Statistik: Memilih uji statistik yang tepat berdasarkan desain penelitian, jenis data (nominal, ordinal, interval, rasio), dan distribusi data (normal atau tidak normal).
3. Pengumpulan dan Pengolahan Data: Mengumpulkan data yang relevan dan mengolahnya untuk mempersiapkan analisis statistik. Ini termasuk membersihkan data dari kesalahan dan melakukan transformasi data jika diperlukan.
4. Pelaksanaan Uji Statistik: Melakukan perhitungan uji statistik yang telah dipilih menggunakan software statistik atau kalkulator.
5. Interpretasi Hasil: Menganalisis hasil uji statistik, termasuk nilai p-value dan statistik uji, untuk menentukan apakah hipotesis nol ditolak atau diterima.

Contoh Prosedur Uji t-test

Uji t-test digunakan untuk membandingkan rata-rata dua kelompok data. Misalnya, kita ingin membandingkan tinggi badan siswa laki-laki dan perempuan di suatu sekolah. Berikut langkah-langkahnya:

1. Hipotesis: H0: Tidak ada perbedaan rata-rata tinggi badan antara siswa laki-laki dan perempuan. H1: Ada perbedaan rata-rata tinggi badan antara siswa laki-laki dan perempuan.
2. Pemilihan Uji: Uji t-test independent samples karena kita membandingkan dua kelompok yang independen.
3. Pengumpulan Data: Mengumpulkan data tinggi badan siswa laki-laki dan perempuan.
4. Pelaksanaan Uji: Masukkan data ke dalam software statistik (misalnya SPSS, R) dan jalankan uji t-test independent samples. Software akan menghitung nilai t-statistik dan p-value.
5. Interpretasi: Jika p-value < 0.05, kita tolak H0 dan simpulkan ada perbedaan signifikan antara rata-rata tinggi badan siswa laki-laki dan perempuan. Jika p-value ≥ 0.05, kita gagal menolak H0 dan simpulkan tidak ada perbedaan signifikan.

Perhitungan Nilai p-value

Nilai p-value merupakan probabilitas mendapatkan hasil yang sama ekstrem atau lebih ekstrem daripada hasil yang diamati, dengan asumsi hipotesis nol benar. Perhitungan p-value bergantung pada uji statistik yang digunakan. Software statistik biasanya akan menghitung nilai p-value secara otomatis. Secara umum, semakin kecil nilai p-value, semakin kuat bukti untuk menolak hipotesis nol.

Nilai p-value yang rendah (biasanya kurang dari 0.05) mengindikasikan bukti yang cukup kuat untuk menolak hipotesis nol. Namun, perlu diingat bahwa tingkat signifikansi (alpha) dapat disesuaikan tergantung konteks penelitian. Nilai p-value harus diinterpretasikan bersamaan dengan besarnya efek dan konteks penelitian.

Pemilihan Uji Statistik yang Tepat

Pemilihan uji statistik yang tepat sangat penting untuk mendapatkan hasil yang valid dan dapat diinterpretasi dengan benar. Pertimbangan utama adalah desain penelitian dan jenis data. Berikut beberapa contoh:

Desain Penelitian	Jenis Data	Uji Statistik
Membandingkan rata-rata dua kelompok independen	Data interval/rasio, distribusi normal	Uji t-test independent samples
Membandingkan rata-rata dua kelompok berpasangan	Data interval/rasio, distribusi normal	Uji t-test paired samples
Membandingkan rata-rata lebih dari dua kelompok	Data interval/rasio, distribusi normal	ANOVA (Analysis of Variance)
Menguji hubungan antara dua variabel kategorik	Data nominal/ordinal	Uji Chi-square

Interpretasi Hasil Uji Statistik

Interpretasi hasil uji statistik merupakan langkah krusial dalam penelitian. Kemampuan menginterpretasi hasil ini menentukan kesimpulan yang dapat ditarik dan implikasinya bagi penelitian tersebut. Pemahaman yang baik tentang berbagai jenis uji statistik dan cara menginterpretasikan nilai-nilai statistiknya sangat penting untuk menghindari kesimpulan yang salah atau menyesatkan.

Secara umum, interpretasi hasil uji statistik bergantung pada nilai statistik uji (misalnya, t-statistik, F-statistik, chi-square), nilai p (p-value), dan tingkat signifikansi (α) yang telah ditentukan sebelumnya. Nilai p menunjukkan probabilitas mendapatkan hasil yang sama atau lebih ekstrem jika hipotesis nol benar. Jika nilai p lebih kecil dari α (biasanya 0.05), hipotesis nol ditolak, dan hasil uji dianggap signifikan secara statistik.

Sebaliknya, jika nilai p lebih besar dari α, hipotesis nol gagal ditolak.

Interpretasi Hasil Uji Chi-Square

Uji Chi-Square digunakan untuk menguji hubungan antara dua variabel kategorik. Misalnya, kita ingin menguji apakah ada hubungan antara jenis kelamin (laki-laki/perempuan) dan preferensi terhadap jenis musik tertentu (pop/rock). Hasil uji Chi-Square akan memberikan nilai chi-square dan nilai p. Jika nilai p < 0.05, kita dapat menyimpulkan bahwa terdapat hubungan yang signifikan secara statistik antara jenis kelamin dan preferensi musik. Sebaliknya, jika nilai p > 0.05, kita tidak dapat menolak hipotesis nol, yang berarti tidak ada bukti yang cukup untuk menyatakan adanya hubungan signifikan antara kedua variabel tersebut.

Sebagai contoh, bayangkan hasil uji Chi-Square menunjukkan nilai chi-square sebesar 10.5 dan nilai p sebesar 0.01. Dengan tingkat signifikansi 0.05, karena nilai p (0.01) < 0.05, kita menolak hipotesis nol dan menyimpulkan terdapat hubungan signifikan antara jenis kelamin dan preferensi musik. Detail lebih lanjut mengenai kekuatan hubungan dapat dilihat dari ukuran efek (effect size), seperti Cramer's V.

Tabel Interpretasi Nilai Statistik Uji

Uji Statistik	Nilai Statistik	Nilai p	Interpretasi
t-test	Nilai t yang tinggi (positif atau negatif)	p < α (misalnya, 0.05)	Terdapat perbedaan signifikan antara dua kelompok.
t-test	Nilai t mendekati nol	p > α	Tidak terdapat perbedaan signifikan antara dua kelompok.
ANOVA (F-test)	Nilai F yang tinggi	p < α	Terdapat perbedaan signifikan antara tiga atau lebih kelompok.
ANOVA (F-test)	Nilai F rendah	p > α	Tidak terdapat perbedaan signifikan antara tiga atau lebih kelompok.
Chi-Square	Nilai Chi-Square yang tinggi	p < α	Terdapat hubungan signifikan antara dua variabel kategorik.
Chi-Square	Nilai Chi-Square rendah	p > α	Tidak terdapat hubungan signifikan antara dua variabel kategorik.

Implikasi Hasil Uji Statistik yang Signifikan dan Tidak Signifikan

Hasil uji statistik yang signifikan menunjukkan bahwa terdapat bukti yang cukup untuk menolak hipotesis nol. Ini berarti bahwa temuan penelitian mendukung hipotesis alternatif. Sebaliknya, hasil yang tidak signifikan menunjukkan bahwa tidak terdapat cukup bukti untuk menolak hipotesis nol. Hal ini tidak selalu berarti hipotesis nol benar, tetapi hanya menunjukkan bahwa data yang dikumpulkan tidak cukup kuat untuk menolaknya.

Penting untuk diingat bahwa ketiadaan bukti bukanlah bukti ketiadaan.

Pelaporan Hasil Uji Statistik

Pelaporan hasil uji statistik harus dilakukan secara jelas, ringkas, dan akurat. Laporan harus mencakup informasi berikut: jenis uji statistik yang digunakan, nilai statistik uji, derajat kebebasan (jika berlaku), nilai p, dan ukuran efek (jika relevan). Contoh pelaporan yang baik adalah: “Analisis ANOVA menunjukkan perbedaan signifikan antara ketiga kelompok pengobatan (F(2, 27) = 5.67, p = 0.01, η² = 0.30).” Ukuran efek (η²) memberikan gambaran tentang besarnya perbedaan atau hubungan yang ditemukan.

Jenis Data dan Pemilihan Uji Statistik yang Tepat

Memilih uji statistik yang tepat merupakan langkah krusial dalam penelitian kuantitatif. Ketepatan pemilihan uji statistik sangat bergantung pada jenis data yang dikumpulkan dan desain penelitian yang digunakan. Pemahaman yang baik tentang berbagai jenis data dan uji statistik yang sesuai akan memastikan hasil analisis yang valid dan dapat diinterpretasi dengan benar.

Klasifikasi Jenis Data

Data dalam penelitian kuantitatif diklasifikasikan ke dalam empat skala pengukuran: nominal, ordinal, interval, dan rasio. Perbedaan utama terletak pada jenis informasi yang diberikan oleh masing-masing skala dan operasi matematika yang dapat diterapkan.

• Data Nominal: Data kategorikal yang hanya menunjukkan perbedaan kualitatif antara kategori, tanpa urutan atau peringkat. Contoh: jenis kelamin (laki-laki, perempuan), warna mata (hitam, coklat, biru).
• Data Ordinal: Data kategorikal yang menunjukkan urutan atau peringkat, tetapi jarak antara kategori tidak sama atau tidak diketahui. Contoh: tingkat kepuasan (sangat puas, puas, netral, tidak puas, sangat tidak puas), peringkat prestasi (pertama, kedua, ketiga).
• Data Interval: Data numerik yang memiliki jarak yang sama antara kategori, tetapi tidak memiliki titik nol absolut. Contoh: suhu dalam Celcius atau Fahrenheit, tahun.
• Data Rasio: Data numerik yang memiliki jarak yang sama antara kategori dan memiliki titik nol absolut. Contoh: tinggi badan, berat badan, usia, pendapatan.

Alur Pemilihan Uji Statistik

Berikut ini adalah flowchart sederhana yang menggambarkan alur pemilihan uji statistik berdasarkan jenis data dan desain penelitian. Flowchart ini merupakan panduan umum, dan pemilihan uji statistik yang tepat mungkin memerlukan pertimbangan lebih lanjut berdasarkan karakteristik data dan tujuan penelitian.

(Ilustrasi Flowchart: Bayangkan sebuah flowchart yang dimulai dengan pertanyaan “Jenis data apa yang digunakan?”, dengan cabang ke data nominal, ordinal, interval, dan rasio. Setiap cabang kemudian bercabang lagi berdasarkan desain penelitian (misalnya, uji beda, uji korelasi, uji asosiasi). Setiap ujung cabang menunjukkan uji statistik yang sesuai, misalnya, untuk data nominal dan uji beda, dapat menggunakan uji Chi-Square. Untuk data interval/rasio dan uji beda, dapat menggunakan uji-t atau ANOVA. Untuk data interval/rasio dan korelasi, dapat menggunakan korelasi Pearson.)

Tabel Pencocokan Jenis Data dan Uji Statistik

Tabel berikut ini menunjukkan beberapa uji statistik yang umum digunakan berdasarkan jenis data.

Jenis Data	Tujuan Analisis	Uji Statistik	Contoh
Nominal	Uji beda dua kelompok	Uji Chi-Square	Membandingkan proporsi laki-laki dan perempuan yang menyukai produk A
Ordinal	Uji beda dua kelompok	Uji Mann-Whitney U	Membandingkan peringkat kepuasan pelanggan terhadap dua produk yang berbeda
Interval/Rasio	Uji beda satu kelompok	Uji t satu sampel	Membandingkan rata-rata tinggi badan siswa dengan tinggi badan standar
Interval/Rasio	Uji beda dua kelompok	Uji t dua sampel	Membandingkan rata-rata nilai ujian siswa laki-laki dan perempuan

Contoh Kasus Penelitian dan Pemilihan Uji Statistik

Sebuah penelitian ingin menguji pengaruh pemberian pupuk organik terhadap pertumbuhan tinggi tanaman padi. Tinggi tanaman diukur dalam sentimeter setelah 3 bulan pemberian pupuk. Kelompok kontrol tidak diberi pupuk organik, sementara kelompok perlakuan diberi pupuk organik.

Dalam kasus ini, data yang dikumpulkan adalah data rasio (tinggi tanaman dalam sentimeter). Desain penelitian adalah desain eksperimen dengan dua kelompok (kontrol dan perlakuan). Oleh karena itu, uji statistik yang tepat untuk menganalisis data ini adalah uji t dua sampel untuk membandingkan rata-rata tinggi tanaman di antara kedua kelompok.

Uji t dua sampel dipilih karena data berupa data rasio, terdistribusi normal (diasumsikan), dan tujuannya adalah untuk membandingkan rata-rata tinggi tanaman antara dua kelompok yang independen. Uji ini akan memberikan informasi apakah terdapat perbedaan yang signifikan secara statistik antara tinggi tanaman pada kelompok kontrol dan kelompok perlakuan.

Pertimbangan dalam Uji Statistik

Melakukan uji statistik bukanlah sekadar memasukkan data ke dalam software dan membaca hasilnya. Pemahaman yang mendalam tentang asumsi, batasan, dan interpretasi hasil sangat krusial untuk memastikan kesimpulan yang valid dan bermakna. Artikel ini akan membahas beberapa pertimbangan penting yang perlu diperhatikan sebelum, selama, dan setelah melakukan analisis statistik.

Asumsi dalam Uji Statistik Parametrik

Uji statistik parametrik, seperti uji t dan ANOVA, mengandalkan beberapa asumsi yang harus dipenuhi agar hasilnya dapat diinterpretasikan dengan tepat. Pelanggaran asumsi ini dapat menyebabkan hasil yang bias dan tidak akurat. Asumsi-asumsi tersebut antara lain normalitas data, homogenitas varians, dan independensi observasi. Penting untuk memeriksa asumsi-asumsi ini sebelum melakukan uji parametrik.

Potensi Pelanggaran Asumsi dan Cara Mengatasinya

Beberapa metode dapat digunakan untuk memeriksa apakah asumsi uji parametrik terpenuhi. Uji normalitas data dapat dilakukan menggunakan uji Kolmogorov-Smirnov atau Shapiro-Wilk. Homogenitas varians dapat diperiksa dengan uji Levene atau Bartlett. Jika asumsi terlanggar, beberapa solusi dapat dipertimbangkan. Transformasi data, seperti logaritma atau akar kuadrat, dapat membantu menormalkan data yang tidak terdistribusi normal.

Penggunaan uji non-parametrik, yang tidak bergantung pada asumsi distribusi normal, juga merupakan alternatif yang baik. Sebagai contoh, jika asumsi normalitas dilanggar dalam uji t, maka uji non-parametrik seperti uji Mann-Whitney U dapat digunakan sebagai alternatif.

Batasan Uji Statistik

Penting untuk menyadari bahwa uji statistik memiliki batasan. Hasil uji statistik hanya memberikan informasi tentang hubungan antara variabel dalam sampel yang diteliti, dan tidak dapat secara otomatis digeneralisasikan ke populasi yang lebih besar tanpa pertimbangan yang cermat. Ukuran sampel yang kecil dapat mengurangi kekuatan statistik dan meningkatkan kemungkinan kesalahan Tipe II (gagal menolak hipotesis nol yang salah). Selain itu, korelasi tidak sama dengan kausalitas; hubungan statistik antara dua variabel tidak selalu berarti bahwa satu variabel menyebabkan perubahan pada variabel lainnya.

Pemahaman yang kurang baik tentang statistik dapat menyebabkan interpretasi hasil yang salah dan kesimpulan yang keliru.

Ukuran Efek dan Nilai p-value

Nilai p-value seringkali disalahartikan sebagai ukuran kekuatan efek. Nilai p-value hanya menunjukkan probabilitas mendapatkan hasil yang sama atau lebih ekstrim jika hipotesis nol benar. Nilai p-value yang kecil (misalnya, kurang dari 0.05) tidak selalu menunjukkan efek yang besar secara praktis. Oleh karena itu, penting untuk mempertimbangkan ukuran efek, seperti Cohen’s d atau eta-squared, untuk menilai besarnya pengaruh variabel independen terhadap variabel dependen.

Sebagai contoh, nilai p-value yang kecil (misalnya, p = 0.01) mungkin menunjukkan perbedaan yang signifikan secara statistik, namun ukuran efeknya kecil, yang berarti perbedaan tersebut mungkin tidak memiliki arti praktis yang signifikan.

Ringkasan Terakhir

Menguasai uji statistik merupakan kunci keberhasilan dalam penelitian. Panduan ini telah memberikan pemahaman menyeluruh tentang berbagai jenis uji statistik, prosedur pelaksanaannya, dan interpretasi hasilnya. Dengan memahami prinsip-prinsip dasar dan mampu memilih uji statistik yang tepat, peneliti dapat mengolah data secara efektif dan menghasilkan kesimpulan yang valid dan dapat dipertanggungjawabkan. Semoga panduan ini bermanfaat dalam meningkatkan kemampuan analisis data dan menghasilkan penelitian yang berkualitas tinggi.