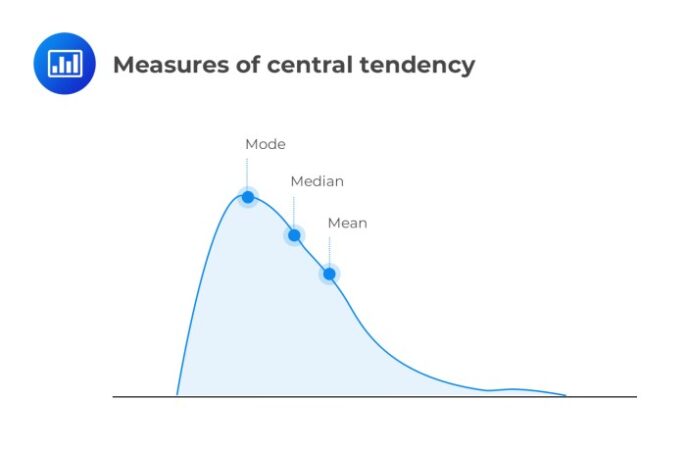
Ukuran pemusatan data merupakan konsep fundamental dalam statistik yang membantu kita memahami karakteristik suatu kumpulan data. Dengan menggunakan mean, median, dan modus, kita dapat merangkum data yang kompleks menjadi satu angka representatif. Bayangkan mencoba memahami pola penjualan suatu produk selama setahun; mean, median, dan modus akan memberikan gambaran yang berbeda namun sama-sama berharga tentang tren penjualan tersebut.
Pemahaman tentang ukuran pemusatan data sangat penting dalam berbagai bidang, mulai dari analisis bisnis dan ekonomi hingga riset kesehatan dan pendidikan. Tiga ukuran pemusatan utama – mean (rata-rata), median (nilai tengah), dan modus (nilai yang paling sering muncul) – masing-masing memiliki keunggulan dan kelemahan yang perlu dipertimbangkan saat memilih ukuran yang paling tepat untuk menggambarkan data.
Ukuran Pemusatan Data
Ukuran pemusatan data merupakan statistik deskriptif yang digunakan untuk merangkum dan menggambarkan kecenderungan pusat dari suatu kumpulan data. Ukuran pemusatan data memberikan gambaran singkat tentang nilai-nilai yang cenderung berada di tengah-tengah data tersebut. Pemahaman tentang ukuran pemusatan data sangat penting dalam berbagai bidang, mulai dari analisis bisnis hingga penelitian ilmiah, karena membantu kita untuk memahami karakteristik utama dari data yang sedang dikaji.
Tujuan utama penggunaan ukuran pemusatan data adalah untuk menyederhanakan data yang kompleks menjadi satu nilai representatif. Nilai ini memudahkan interpretasi dan perbandingan antar kumpulan data yang berbeda. Dengan demikian, kita dapat menarik kesimpulan yang lebih mudah dipahami dan dikomunikasikan.
Contoh Kasus Ukuran Pemusatan Data
Ukuran pemusatan data sering kita temui dalam kehidupan sehari-hari. Berikut beberapa contohnya:
- Penghasilan Rata-rata Karyawan: Perusahaan sering menggunakan mean (rata-rata) untuk menghitung penghasilan rata-rata karyawannya. Informasi ini dapat digunakan untuk perencanaan anggaran, negosiasi gaji, dan analisis kinerja perusahaan.
- Nilai Ujian Tengah Semester: Median (nilai tengah) sering digunakan untuk menggambarkan nilai ujian tengah semester. Median lebih tahan terhadap nilai ekstrem (nilai yang sangat tinggi atau rendah) dibandingkan dengan mean, sehingga memberikan gambaran yang lebih akurat tentang kecenderungan nilai ujian.
- Ukuran Sepatu Terlaris: Modus (nilai yang paling sering muncul) digunakan untuk menentukan ukuran sepatu yang paling banyak terjual di sebuah toko. Informasi ini penting untuk manajemen persediaan dan pengambilan keputusan terkait pembelian barang.
Perbedaan Mean, Median, dan Modus
Mean, median, dan modus merupakan tiga ukuran pemusatan data yang berbeda dan masing-masing memiliki karakteristik unik. Perbedaan mendasar terletak pada cara perhitungan dan kepekaan terhadap nilai ekstrem.
Mean dihitung dengan menjumlahkan semua nilai data kemudian dibagi dengan jumlah data. Median adalah nilai tengah dari data yang telah diurutkan. Modus adalah nilai yang paling sering muncul dalam data. Mean sangat dipengaruhi oleh nilai ekstrem, sedangkan median dan modus relatif lebih tahan terhadap nilai ekstrem.
Perbandingan Mean, Median, dan Modus
| Ukuran Pemusatan | Keunggulan | Kelemahan | Kapan Digunakan |
|---|---|---|---|
| Mean | Mudah dihitung dan dipahami; menggunakan semua data. | Sangat dipengaruhi oleh nilai ekstrem. | Data terdistribusi normal tanpa outlier. |
| Median | Tahan terhadap nilai ekstrem; mudah dihitung untuk data berukuran kecil hingga sedang. | Tidak menggunakan semua data; kurang informatif jika data sangat tersebar. | Data tidak terdistribusi normal atau terdapat outlier. |
| Modus | Mudah diidentifikasi; dapat digunakan untuk data kualitatif. | Tidak selalu ada; mungkin terdapat beberapa modus atau tidak ada modus sama sekali. | Data kategorikal atau untuk menemukan nilai yang paling umum. |
Ilustrasi Perbedaan Mean, Median, dan Modus
Bayangkan data penjualan rumah di suatu daerah dalam satu bulan: Rp 500 juta, Rp 600 juta, Rp 650 juta, Rp 700 juta, dan Rp 2 miliar. Mean (rata-rata) penjualan adalah Rp 810 juta. Namun, nilai Rp 2 miliar yang sangat tinggi ini menggerus representasi data secara keseluruhan. Median (nilai tengah) adalah Rp 650 juta, yang memberikan gambaran yang lebih realistis tentang harga rumah yang terjual.
Modus, dalam kasus ini, mungkin tidak ada karena tidak ada harga yang berulang. Contoh ini menunjukkan bagaimana mean dapat menyesatkan jika terdapat nilai ekstrem, sementara median memberikan gambaran yang lebih robust dan representatif.
Perhitungan Mean, Median, dan Modus
Ukuran pemusatan data, yaitu mean, median, dan modus, merupakan statistik deskriptif yang penting untuk memahami karakteristik suatu kumpulan data. Ketiganya memberikan gambaran berbeda tentang pusat data, dan pemahaman masing-masing sangat berguna dalam berbagai konteks analisis data.
Perhitungan Mean
Mean, atau rata-rata, dihitung dengan menjumlahkan semua nilai data kemudian dibagi dengan jumlah data. Perhitungannya berbeda sedikit antara data tunggal dan data kelompok.
- Data Tunggal: Jumlah semua nilai data dibagi dengan banyaknya data. Misalnya, untuk data 2, 4, 6, 8, 10, mean-nya adalah (2+4+6+8+10)/5 = 6.
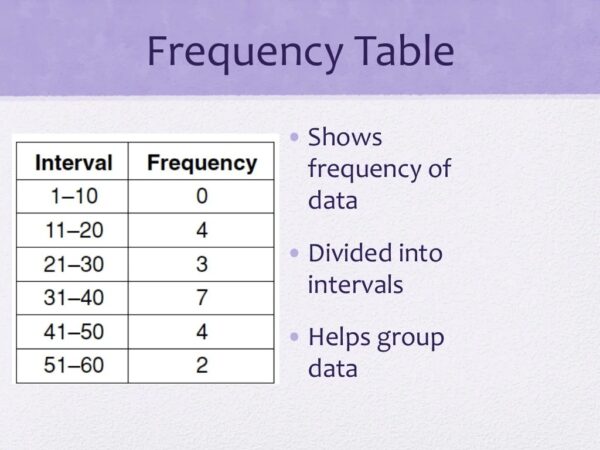
- Data Kelompok: Karena data dikelompokkan dalam interval kelas, kita menggunakan titik tengah setiap kelas sebagai representasi nilai data dalam kelas tersebut. Kemudian, kita mengalikan titik tengah setiap kelas dengan frekuensi kelasnya, menjumlahkan hasil perkalian tersebut, dan membaginya dengan jumlah total frekuensi.
Perhitungan Median, Ukuran pemusatan data
Median merupakan nilai tengah dari suatu data setelah diurutkan dari nilai terkecil hingga terbesar. Cara perhitungannya bergantung pada apakah jumlah data ganjil atau genap.
- Data Tunggal (Ganjil): Nilai tengah langsung menjadi median. Misalnya, untuk data 2, 4, 6, 8, 10, mediannya adalah 6.
- Data Tunggal (Genap): Median adalah rata-rata dari dua nilai tengah. Misalnya, untuk data 2, 4, 6, 8, mediannya adalah (4+6)/2 = 5.
- Data Kelompok: Median dihitung dengan menggunakan rumus interpolasi, mempertimbangkan frekuensi kumulatif dan lebar interval kelas yang memuat median.
Perhitungan Modus
Modus adalah nilai yang paling sering muncul dalam suatu data. Modus dapat berupa satu nilai, lebih dari satu nilai (multimodal), atau tidak ada modus (jika semua nilai muncul dengan frekuensi yang sama).
- Data Tunggal: Nilai yang paling sering muncul. Misalnya, pada data 2, 4, 4, 6, 8, modus adalah 4.
- Data Kelompok: Kelas dengan frekuensi tertinggi disebut modus. Perlu diingat bahwa ini hanya memberikan perkiraan nilai modus, bukan nilai modus yang tepat.
Contoh Perhitungan Mean, Median, dan Modus
Nilai ujian 10 siswa: 70, 80, 75, 90, 85, 70, 95, 80, 75, 85
Mean: (70+80+75+90+85+70+95+80+75+85)/10 = 80
Data setelah diurutkan: 70, 70, 75, 75, 80, 80, 85, 85, 90, 95
Median: (80+80)/2 = 80
Modus: 70, 75, 80, dan 85 (multimodal)
Contoh Data dengan Mean, Median, dan Modus Berbeda
Perhatikan data berikut: 1, 2, 2, 3, 100. Meannya adalah (1+2+2+3+100)/5 = 21.6. Mediannya adalah 2. Modusnya adalah 2. Dalam kasus ini, nilai ekstrim (100) mempengaruhi mean secara signifikan, sementara median dan modus kurang terpengaruh oleh nilai ekstrim tersebut.
Hal ini menunjukkan bahwa mean sensitif terhadap outlier, sedangkan median dan modus lebih robust terhadap outlier.
Interpretasi Ukuran Pemusatan Data
Mean, median, dan modus, ketiganya merupakan ukuran pemusatan data yang umum digunakan dalam statistika deskriptif. Meskipun semuanya bertujuan untuk menunjukkan nilai pusat dari suatu kumpulan data, interpretasi masing-masing ukuran dapat memberikan informasi yang berbeda dan bahkan saling bertentangan, tergantung pada distribusi data yang dianalisis. Pemahaman perbedaan ini krusial dalam memilih ukuran pemusatan data yang tepat dan menghindari kesimpulan yang keliru.
Pemilihan ukuran pemusatan data yang tepat bergantung pada karakteristik data dan tujuan analisis. Data yang terdistribusi normal akan menunjukkan nilai mean, median, dan modus yang relatif sama. Namun, pada data yang memiliki outlier atau distribusi yang miring, interpretasi ketiga ukuran ini akan memberikan gambaran yang berbeda.
Mean Lebih Representatif daripada Median dan Modus
Mean (rata-rata) menjadi ukuran yang lebih representatif ketika data terdistribusi secara normal atau mendekati normal, tanpa adanya outlier yang signifikan. Mean mempertimbangkan semua nilai data dalam perhitungannya, sehingga memberikan gambaran yang komprehensif tentang nilai pusat data.
Contoh: Misalnya, nilai ujian matematika dari 10 siswa adalah: 70, 75, 80, 80, 85, 85, 90, 90, 95, 100. Mean dari data ini adalah 85. Nilai ini memberikan gambaran yang baik tentang kinerja rata-rata siswa. Median dan modus juga sama-sama 85, sehingga ketiganya memberikan kesimpulan yang sama.
Median Lebih Representatif daripada Mean dan Modus
Median (nilai tengah) lebih representatif ketika data mengandung outlier atau memiliki distribusi yang sangat miring. Outlier dapat secara signifikan mempengaruhi nilai mean, sehingga median menjadi pilihan yang lebih robust dan akurat dalam mewakili nilai pusat data.
Contoh: Misalnya, harga rumah di suatu daerah adalah: 500 juta, 600 juta, 650 juta, 700 juta, 750 juta, 800 juta, 2 miliar. Mean harga rumah adalah 866,67 juta, sedangkan mediannya adalah 700 juta. Adanya outlier (2 miliar) sangat mempengaruhi nilai mean, sehingga median memberikan gambaran yang lebih realistis tentang harga rumah di daerah tersebut.
Modus Lebih Representatif daripada Mean dan Median
Modus (nilai yang paling sering muncul) paling representatif ketika kita tertarik pada nilai yang paling umum atau populer dalam suatu kumpulan data. Modus tidak terpengaruh oleh outlier dan cocok untuk data kategorikal atau data numerik dengan distribusi yang multimodal (memiliki beberapa puncak).
Contoh: Misalnya, ukuran sepatu yang paling sering terjual di sebuah toko sepatu adalah ukuran 40. Meskipun mean dan median ukuran sepatu yang terjual mungkin berbeda, modus (ukuran 40) memberikan informasi yang paling relevan bagi toko tersebut, yaitu ukuran yang paling banyak diminati konsumen.
Pengaruh Pemilihan Ukuran Pemusatan Data terhadap Kesimpulan Analisis
Pemilihan ukuran pemusatan data yang tidak tepat dapat menyebabkan kesimpulan analisis yang keliru. Sebagai contoh, jika kita menggunakan mean untuk menganalisis data harga rumah dengan outlier yang signifikan, kita akan mendapatkan gambaran yang bias dan tidak realistis tentang harga rumah rata-rata di daerah tersebut. Sebaliknya, penggunaan median akan memberikan gambaran yang lebih akurat dan representatif.
Contoh: Bayangkan sebuah perusahaan ingin menganalisis gaji karyawannya. Jika perusahaan menggunakan mean gaji, dan terdapat beberapa eksekutif dengan gaji sangat tinggi, maka mean akan memberikan gambaran gaji rata-rata yang jauh lebih tinggi daripada gaji mayoritas karyawan. Ini dapat memberikan kesan bahwa karyawan mendapatkan gaji yang tinggi, padahal kenyataannya tidak demikian. Dalam kasus ini, median gaji akan memberikan gambaran yang lebih akurat tentang gaji rata-rata karyawan.
Penggunaan Ukuran Pemusatan Data dalam Berbagai Konteks

Ukuran pemusatan data, seperti mean, median, dan modus, merupakan alat statistik vital yang memberikan gambaran ringkas tentang kumpulan data. Kegunaannya meluas ke berbagai bidang, memberikan wawasan berharga untuk pengambilan keputusan yang lebih efektif dan informatif. Pemahaman akan nilai tengah data ini sangat krusial dalam interpretasi data dan analisis tren. Berikut beberapa penerapannya di berbagai sektor.
Penerapan Ukuran Pemusatan Data dalam Bidang Ekonomi
Dalam ekonomi, ukuran pemusatan data digunakan secara luas untuk menganalisis berbagai aspek, mulai dari pendapatan nasional hingga harga pasar. Misalnya, rata-rata pendapatan per kapita suatu negara dapat memberikan gambaran umum tentang kesejahteraan ekonomi penduduknya. Median pendapatan lebih tahan terhadap nilai ekstrem (misalnya, pendapatan miliarder) dan memberikan gambaran yang lebih akurat tentang pendapatan mayoritas penduduk. Modus dapat menunjukkan harga produk yang paling sering diperjualbelikan di pasar.
Analisis tren harga komoditas juga sering memanfaatkan mean untuk mengidentifikasi fluktuasi harga dan memprediksi harga di masa depan. Data inflasi, misalnya, sering dirata-ratakan untuk melihat tren inflasi jangka panjang. Penggunaan median dan modus juga relevan untuk melihat distribusi harga yang lebih detail dan menghindari distorsi akibat harga ekstrem.
Penerapan Ukuran Pemusatan Data dalam Bidang Kesehatan
Di bidang kesehatan, ukuran pemusatan data penting untuk memantau kesehatan masyarakat dan mengevaluasi efektivitas pengobatan. Misalnya, rata-rata tekanan darah pasien dapat digunakan untuk menilai kesehatan jantung mereka. Median usia pasien yang terinfeksi penyakit tertentu dapat memberikan wawasan tentang kelompok usia yang paling rentan. Modus dapat menunjukkan gejala yang paling umum terjadi pada suatu penyakit.
Studi epidemiologi sering menggunakan ukuran pemusatan data untuk menganalisis penyebaran penyakit. Misalnya, rata-rata angka kematian akibat suatu penyakit tertentu dapat menunjukkan tingkat keparahan penyakit tersebut. Median lamanya perawatan pasien di rumah sakit dapat membantu dalam perencanaan sumber daya kesehatan. Modus dapat mengidentifikasi jenis penyakit yang paling sering didiagnosis di suatu wilayah.
Penerapan Ukuran Pemusatan Data dalam Bidang Pendidikan
Dalam dunia pendidikan, ukuran pemusatan data digunakan untuk mengevaluasi kinerja siswa dan efektivitas program pembelajaran. Rata-rata nilai ujian siswa dapat menunjukkan pemahaman mereka terhadap materi pelajaran. Median nilai ujian lebih tahan terhadap nilai ekstrem dan memberikan gambaran yang lebih akurat tentang kinerja mayoritas siswa. Modus dapat menunjukkan nilai ujian yang paling sering muncul.
Ukuran pemusatan data juga dapat digunakan untuk membandingkan kinerja siswa di berbagai sekolah atau kelas. Analisis ini membantu dalam mengidentifikasi area yang perlu ditingkatkan dalam kurikulum atau metode pengajaran. Misalnya, perbandingan rata-rata nilai ujian matematika antar sekolah dapat menunjukkan perbedaan kualitas pendidikan di berbagai wilayah.
Studi Kasus: Analisis Kepuasan Pelanggan terhadap Sebuah Restoran
Sebuah restoran ingin menganalisis kepuasan pelanggannya berdasarkan survei yang dilakukan. Survei tersebut menggunakan skala 1-5, dengan 5 sebagai kepuasan tertinggi. Hasil survei menunjukkan data berikut: 3, 4, 5, 5, 4, 3, 2, 5, 4, 4, 5, 3, 4, 5, 5.
Dengan menggunakan ukuran pemusatan data, kita dapat menganalisis data tersebut:
- Mean: 4.13 (rata-rata kepuasan pelanggan cukup tinggi)
- Median: 4 (separuh pelanggan memberikan nilai 4 atau lebih)
- Modus: 5 (nilai kepuasan yang paling sering muncul)
Dari hasil analisis, dapat disimpulkan bahwa mayoritas pelanggan merasa puas dengan restoran tersebut, dengan nilai kepuasan tertinggi paling sering muncul.
Laporan Singkat Analisis Kepuasan Pelanggan
Judul: Analisis Kepuasan Pelanggan Restoran “X”
Metode: Survei kepuasan pelanggan menggunakan skala 1-5.
Hasil: Data yang dikumpulkan dianalisis menggunakan mean, median, dan modus. Mean kepuasan pelanggan adalah 4.13, median 4, dan modus 5.
Interpretasi: Hasil menunjukkan tingkat kepuasan pelanggan yang tinggi. Rata-rata kepuasan mendekati nilai tertinggi, dan nilai modus menunjukkan bahwa sebagian besar pelanggan memberikan penilaian tertinggi.
Kesimpulan: Restoran “X” secara umum telah berhasil memenuhi harapan pelanggan. Namun, upaya peningkatan kualitas layanan tetap perlu dilakukan untuk mempertahankan tingkat kepuasan pelanggan yang tinggi.
Penutup: Ukuran Pemusatan Data
Kesimpulannya, pemilihan ukuran pemusatan data yang tepat sangat bergantung pada karakteristik data dan tujuan analisis. Memahami perbedaan antara mean, median, dan modus, serta keunggulan dan kelemahan masing-masing, merupakan kunci dalam menginterpretasi data secara akurat dan mengambil kesimpulan yang bermakna. Dengan pemahaman yang baik, kita dapat menggunakan ukuran pemusatan data untuk membuat keputusan yang lebih tepat dan efektif dalam berbagai konteks.